2022--2023学年人教版七年级数学上册24.1 圆 同步测试题 (含答案)
文档属性
| 名称 | 2022--2023学年人教版七年级数学上册24.1 圆 同步测试题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 307.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 16:09:52 | ||
图片预览




文档简介
24.1圆的同步作业
选择题
下列命题正确的有()
①弦是圆上任意两点之间的部分②半径是弦③直径是最长的弦④弧是半圆,半圆是 弧
1 个 B. 2个 C. 3个 D.4个
如图所示,MN为⊙O的弦,∠N=520,则∠MON的度数为( )
380 B.520 C.760 D.1040
如图,已知CD为⊙O的直径,过点D的弦DE平等于半径OA,若∠D的度数是500,则∠C的度数是( )
250 B.400 C.300 D.500
一个点到圆上的最小距离是4cm,最大距离是9cm,则圆的半径是( )
A.2.5cm或6.5cm B.2.5cm C. 6.5cm D.5cm或13cm
如图,已知在⊙O中,AB、CD为直径,同AD与BC的关系是( )
AD=BC B.AD∥BC C.AD∥BC且AD=BC D.不能确定
如图,已知AB为⊙O的直径,点C在⊙O上,∠C=150,则∠BOC的度数为( )
A.150 B.300 C.450 D. 600
填空题
⊙O的半径为2cm,则它的弦长dcm的取值范围是________.
⊙O中若弦AB等于⊙O的半径,则△AOB的形状是________
如图,已知AB是⊙O的直径,点C在⊙O上,点D是BC的中点,若AC=10cm,则OD_____cm
如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=180,
∠C=______, ∠AOC=________;
11.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最长弦长为______,最短弦长为_______;
解答题
12.在Rt△ABC中,∠C=900,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何?
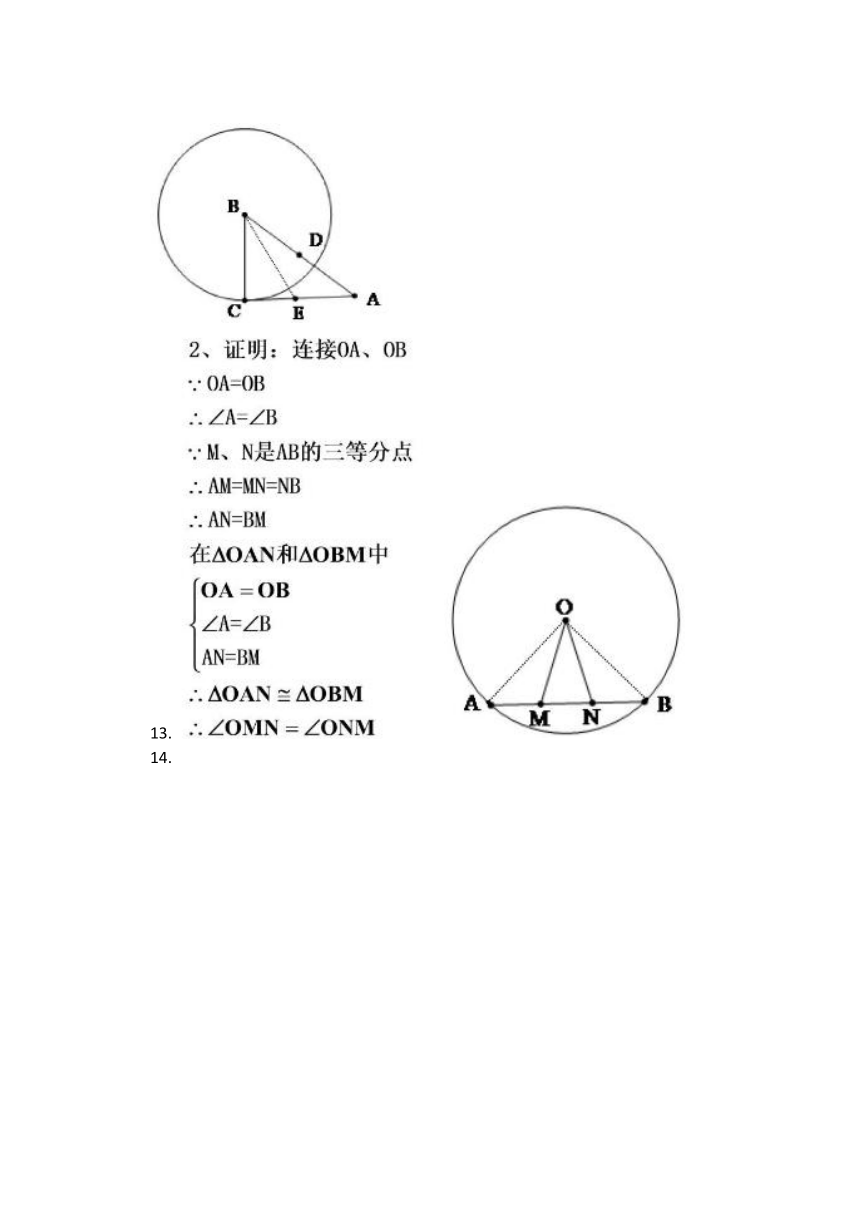
13.如图,M,N为线段AB上的两个三等分点,点A、B在⊙O上,
求证:∠OMN=∠ONM
14.如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=180,求∠AOC的度数
参考答案
选择题
A 2.C 3.A 4.A 5.C 6.B
填空题
0等边三角形
5
360,1080
10,8
解答题
12.
12.
13.
14.
24.1圆的同步作业
选择题
下列命题正确的有()
①弦是圆上任意两点之间的部分②半径是弦③直径是最长的弦④弧是半圆,半圆是 弧
1 个 B. 2个 C. 3个 D.4个
如图所示,MN为⊙O的弦,∠N=520,则∠MON的度数为( )
380 B.520 C.760 D.1040
如图,已知CD为⊙O的直径,过点D的弦DE平等于半径OA,若∠D的度数是500,则∠C的度数是( )
250 B.400 C.300 D.500
一个点到圆上的最小距离是4cm,最大距离是9cm,则圆的半径是( )
A.2.5cm或6.5cm B.2.5cm C. 6.5cm D.5cm或13cm
如图,已知在⊙O中,AB、CD为直径,同AD与BC的关系是( )
AD=BC B.AD∥BC C.AD∥BC且AD=BC D.不能确定
如图,已知AB为⊙O的直径,点C在⊙O上,∠C=150,则∠BOC的度数为( )
A.150 B.300 C.450 D. 600
填空题
⊙O的半径为2cm,则它的弦长dcm的取值范围是________.
⊙O中若弦AB等于⊙O的半径,则△AOB的形状是________
如图,已知AB是⊙O的直径,点C在⊙O上,点D是BC的中点,若AC=10cm,则OD_____cm
P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最长弦长为______,最短弦长为_______;
解答题
11.在Rt△ABC中,∠C=900,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何?
12.如图,M,N为线段AB上的两个三等分点,点A、B在⊙O上,
求证:∠OMN=∠ONM
13.如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=180,求∠AOC的度数
参考答案
选择题
A 2.C 3.A 4.A 5.C 6.B
填空题
0等边三角形
5
10,8
解答题
解:连接BE
∵∠C=900,BC=3cm,AC=4cm
∴AB==5cm
∵D是AB的中点
∴BD=
∵是AC的中点
∴CE=
∴BE==cm
∴BA>BC,BE>BC,BD∴点A、E均在⊙B外;点D在⊙B内;点C在⊙B上。
证明:连接OA、OB
∵OA=OB
∴∠A=∠B
∵M、N是AB的三等分点
∴AM=MN=NB
∴AN=BM
∴△OAN≌△OBM
∴∠OMN=∠ONM
解:连接OD
∵AB=2DE,AB=2OD
∴OD=DE
∴∠EOD=∠E=180
∴∠CDO=2∠E=360
∵OC=OD
∴∠OCD=360
∴∠AOC=∠E+∠C=540
选择题
下列命题正确的有()
①弦是圆上任意两点之间的部分②半径是弦③直径是最长的弦④弧是半圆,半圆是 弧
1 个 B. 2个 C. 3个 D.4个
如图所示,MN为⊙O的弦,∠N=520,则∠MON的度数为( )
380 B.520 C.760 D.1040
如图,已知CD为⊙O的直径,过点D的弦DE平等于半径OA,若∠D的度数是500,则∠C的度数是( )
250 B.400 C.300 D.500
一个点到圆上的最小距离是4cm,最大距离是9cm,则圆的半径是( )
A.2.5cm或6.5cm B.2.5cm C. 6.5cm D.5cm或13cm
如图,已知在⊙O中,AB、CD为直径,同AD与BC的关系是( )
AD=BC B.AD∥BC C.AD∥BC且AD=BC D.不能确定
如图,已知AB为⊙O的直径,点C在⊙O上,∠C=150,则∠BOC的度数为( )
A.150 B.300 C.450 D. 600
填空题
⊙O的半径为2cm,则它的弦长dcm的取值范围是________.
⊙O中若弦AB等于⊙O的半径,则△AOB的形状是________
如图,已知AB是⊙O的直径,点C在⊙O上,点D是BC的中点,若AC=10cm,则OD_____cm
如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=180,
∠C=______, ∠AOC=________;
11.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最长弦长为______,最短弦长为_______;
解答题
12.在Rt△ABC中,∠C=900,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何?
13.如图,M,N为线段AB上的两个三等分点,点A、B在⊙O上,
求证:∠OMN=∠ONM
14.如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=180,求∠AOC的度数
参考答案
选择题
A 2.C 3.A 4.A 5.C 6.B
填空题
0
5
360,1080
10,8
解答题
12.
12.
13.
14.
24.1圆的同步作业
选择题
下列命题正确的有()
①弦是圆上任意两点之间的部分②半径是弦③直径是最长的弦④弧是半圆,半圆是 弧
1 个 B. 2个 C. 3个 D.4个
如图所示,MN为⊙O的弦,∠N=520,则∠MON的度数为( )
380 B.520 C.760 D.1040
如图,已知CD为⊙O的直径,过点D的弦DE平等于半径OA,若∠D的度数是500,则∠C的度数是( )
250 B.400 C.300 D.500
一个点到圆上的最小距离是4cm,最大距离是9cm,则圆的半径是( )
A.2.5cm或6.5cm B.2.5cm C. 6.5cm D.5cm或13cm
如图,已知在⊙O中,AB、CD为直径,同AD与BC的关系是( )
AD=BC B.AD∥BC C.AD∥BC且AD=BC D.不能确定
如图,已知AB为⊙O的直径,点C在⊙O上,∠C=150,则∠BOC的度数为( )
A.150 B.300 C.450 D. 600
填空题
⊙O的半径为2cm,则它的弦长dcm的取值范围是________.
⊙O中若弦AB等于⊙O的半径,则△AOB的形状是________
如图,已知AB是⊙O的直径,点C在⊙O上,点D是BC的中点,若AC=10cm,则OD_____cm
P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最长弦长为______,最短弦长为_______;
解答题
11.在Rt△ABC中,∠C=900,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何?
12.如图,M,N为线段AB上的两个三等分点,点A、B在⊙O上,
求证:∠OMN=∠ONM
13.如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=180,求∠AOC的度数
参考答案
选择题
A 2.C 3.A 4.A 5.C 6.B
填空题
0
5
10,8
解答题
解:连接BE
∵∠C=900,BC=3cm,AC=4cm
∴AB==5cm
∵D是AB的中点
∴BD=
∵是AC的中点
∴CE=
∴BE==cm
∴BA>BC,BE>BC,BD
证明:连接OA、OB
∵OA=OB
∴∠A=∠B
∵M、N是AB的三等分点
∴AM=MN=NB
∴AN=BM
∴△OAN≌△OBM
∴∠OMN=∠ONM
解:连接OD
∵AB=2DE,AB=2OD
∴OD=DE
∴∠EOD=∠E=180
∴∠CDO=2∠E=360
∵OC=OD
∴∠OCD=360
∴∠AOC=∠E+∠C=540
同课章节目录
