13.3.2等边三角形
图片预览








文档简介
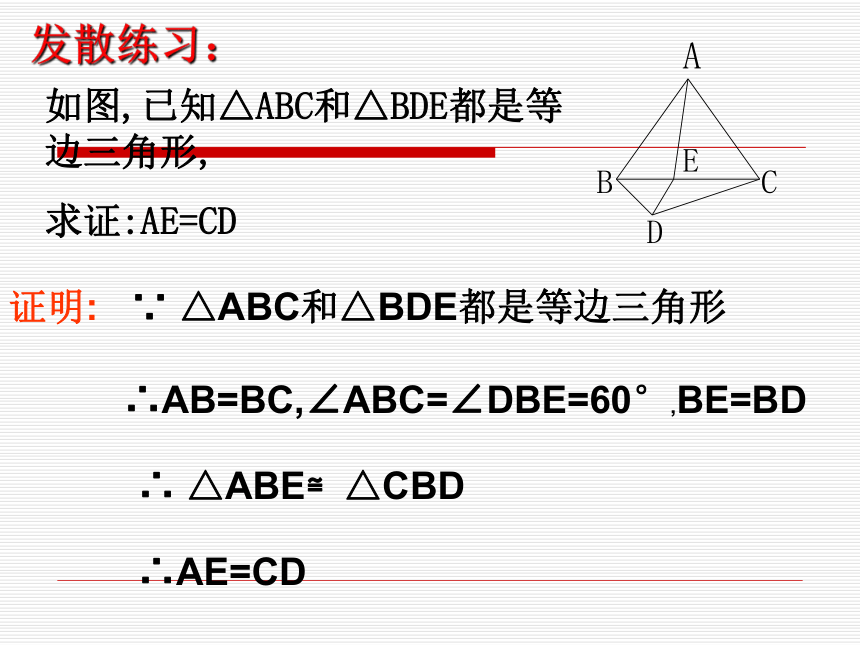
课件34张PPT。1、等腰三角形的性质定理是什么?性质1:等腰三角形的两个底角相等。(等边对等角)性质2: 等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。2、等腰三角形的判定定理:如果一个三角形中有两个角相等,那么这两个角所对的边也相等.(简称为:等角对等边 )一、温故知新等边三角形性质: 等边三角形的各边都相等,各角都相等并且每一个角都等于60°,各边都相等,是轴对称图形且有三条对称轴.判定1:三条边都相等的三角形是等边三角形。判定3: 有一个角是60°的等腰三角形是等边三角形.一、温故知新判定2:三个角都相等的三角形是等边三角形。如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD证明:∵ △ABC和△BDE都是等边三角形∴AB=BC,∠ABC=∠DBE=60°,BE=BD∴ △ABE≌△CBD∴AE=CD发散练习:第十三章 轴对称13.3.2等边三角形 问题 已知△ABC 中,∠A =60°,( ?????? ?).
请你在括号内补充一个条件,使△ABC 能成为等边三角
形.∠B =60°(或∠C =60°)
AB =BC、AC =BC、AB =BC =AC 创设情境,导入新知 思考2 这个特殊的直角三角形相比一般的直角三角形有什么不同之处,它有什么特殊性质?创设情境,导入新知 思考1 等边三角形是轴对称图形,若沿着其中一
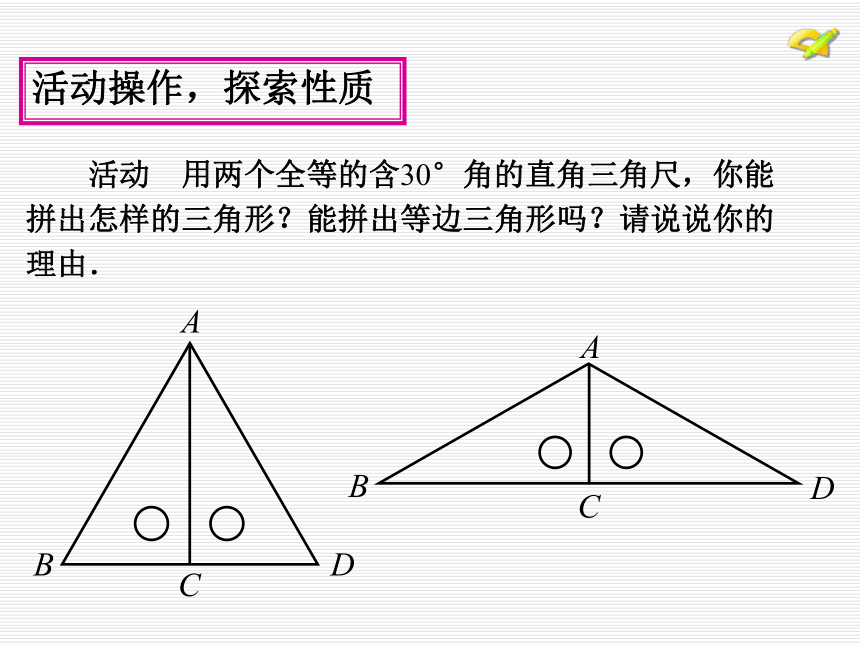
条对称轴折叠,能产生什么特殊图形? 活动 用两个全等的含30°角的直角三角尺,你能
拼出怎样的三角形?能拼出等边三角形吗?请说说你的
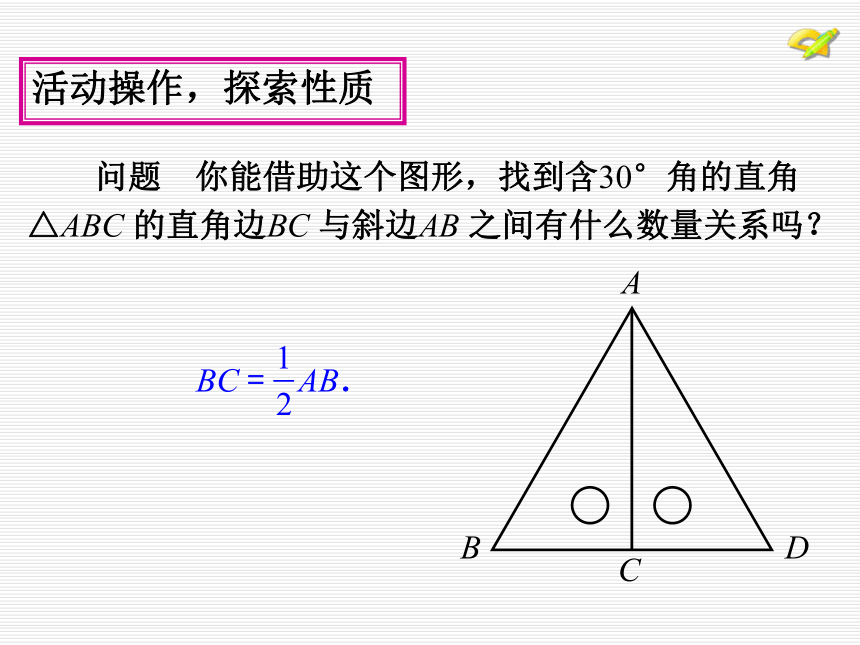
理由. 活动操作,探索性质BC = AB. 活动操作,探索性质 问题 你能借助这个图形,找到含30°角的直角
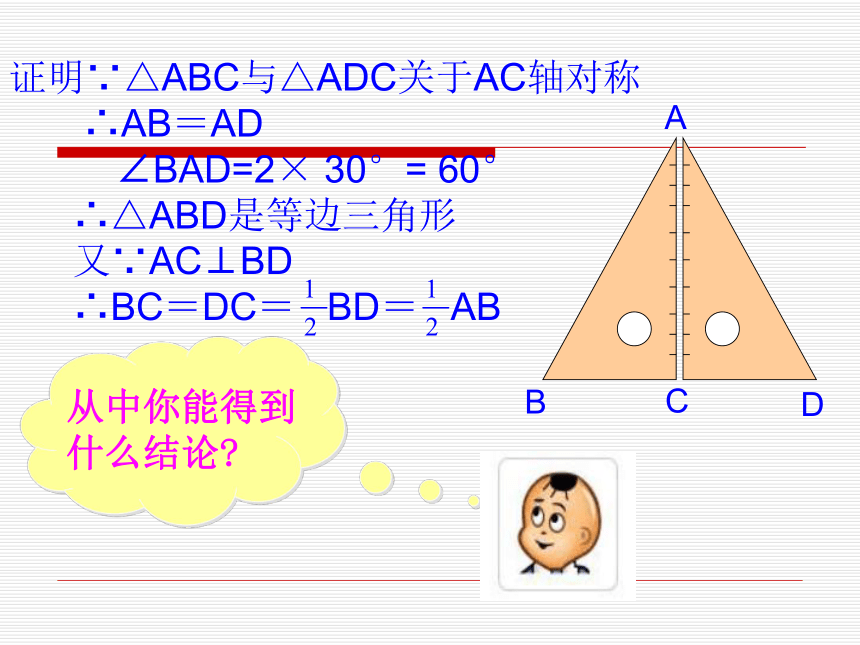
△ABC 的直角边BC 与斜边AB 之间有什么数量关系吗? 证明∵△ABC与△ADC关于AC轴对称
∴AB=AD
∠BAD=2× 30°= 60°
∴△ABD是等边三角形
又∵AC⊥BD
∴BC=DC= BD= AB从中你能得到
什么结论? 思考 这个命题是真命题吗?请进行证明. 问题 请说一说你猜想的命题中,条件和结论分别是什么?并结合图形,用符号语言表述出来.活动操作,探索性质 猜想 在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半.证明:在△ABC 中,
∵ ∠C =90°,∠A =30°,
∴ ∠B =60°.
延长BC 到D,使BD =AB,
连接AD,
则△ABD 是等边三角形. 已知:如图,在Rt△ABC 中,∠C =90°,∠A =
30°. 求证:BC = AB.活动操作,探索性质∴ BC = BD = AB . 已知:如图,在Rt△ABC 中,∠C =90°,∠A =
30°. 求证:BC = AB. 追问:你还能用其他方
法证明吗? 活动操作,探索性质证明:由等边三角形的性质可知,
AC 也是BD 边上的中线,动手操作,探索性质另证:作∠BCE =60°,交AB于E,连接CE, 则∠ACE =90°-60°=30°.
在△ABC 中,
∵ ∠ACB=90°,∠A =30°,
∴ ∠B =60°.
在△BCE 中,
∵ ∠BCE=60°,∠B =60°,
∴ △BCE 是等边三角形.
∴ BC =BE =CE.动手操作,探索性质∴ BC =BE =AE = AB. 另证:
在△ACE 中,
∵ ∠A=30°,∠ACE =30°,
∴ △AEC是等腰三角形.
∴ CE =AE.
∴ BC =BE =CE =AE.符号语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°, 动手操作,探索性质 在直角三角形中,如果一个锐角等于30°,那么
它所对的直角边等于斜边的一半.∴ BC = AB. 定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.在Rt△ABC中
∵∠A=30°
∴AB=2BCABC300这又是一个判定两条线段成倍分关系的根据之一.5课堂练习 练习1 如图,在△ABC 中,∠C =90°,∠A =
30°,AB =10,则BC 的长为 .1课堂练习 练习2 如图,在△ABC 中,∠ACB =90°,CD 是
高,∠A =30°,AB =4.则BD = . 思考 图中BC、DE 分
别是哪个直角三角形的直角
边?它们所对的锐角分别是
多少度? 性质运用 例 如图是屋架设计图的一部分,点D 是斜梁AB
的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,
∠A =30°,立柱BC、DE 要多长?解:∵DE⊥AC, BC⊥AC, ∠A=30°
可得 BC= AB, DE= AD
∴BC= ×7.4=3.7m
又 AD= AB
∴DE= AD= ×3.7=1.85m
答:立柱BC的长是3.7m,DE的长是1.85m.这又是一个判定两条线段成倍分关系的根据之一.记住哟′解:过C作BA延长线的垂线CD,垂足为D
∵∠B=∠ACB=150(已知),
∴∠DAC=∠B+∠ACB= 150+150=300
(三角形的一个外角,等于和它不相邻的两内角的和).
∴CD= AC= ×2a=a
(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半).ACBD150150例2.已知:等腰三角形的底角为150,腰长为2a.
求:腰上的高.2a例3.已知:如图,在△ABC中,∠ACB=900,∠A=300,CD⊥AB于D.
求证:BD= AB.你能规范地写出证明过程吗?你的证题能力有所提高吗?ACBD反过来怎么样——逆向思维命题:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.是真命题吗?
如果是,请你证明它.ABC已知:如图,在△ABC中,∠ACB=900,BC= AB.
求证:∠A=300.反过来怎么样——逆向思维在△ABD中,∵∠ACB=900(已知),
∴AB=AD(线段垂直平分线上的点到线段两端的距离相等).
又∵BC=AB/2(已知),
BC=BD/2(作图),
∴AB=BD(等量代换).
∴AB=BD=AD(等式性质).
∴△ABD是等边三角形(等边三角形定义).
∴∠B=600(等边三角形定义).
∴∠A=300(直角三角形两锐角互余).300ABC证明:如图, 延长BC至D,使CD=BC,连接AD.几何的三种语言′这是一个通过线段之间的关系来判定一个角的具体度数(300)的根据之一.定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.在△ABC中
∵∠ACB=900,BC=AB/2(已知),
∴∠A=300(在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300).比一比:看 谁 算 的 快1.如图:在Rt△ABC中
∠A=300,AB+BC=12cm
则AB=_____cm82.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm, BD=___, BE=____4cm 2cm挑战自我:相信你一定能行2.如图:已知 在△ABC 中,∠A=300,C=900,BD平分∠ABC.
求证:AD=2DC1.如图,在△ABC中,∠C=900,∠B=150, DE是AB的中垂线,BE=5,
则AE=______,AC=_____成功者的摇篮1.如图(1):四边形ABCD是一张正方形纸片,E,F分别是AB,CD的中点,沿着过点D的折痕将A角翻折,使得A落在EF上(如图(2)), 折痕交AE于点G,那么∠ADG等于多少度?你能证明你的结论吗?DACBEF(1)(2)GA成功者的摇篮答:∠ADG等于150. 证明:∵DF=DC/2(中点定义),A1D=AD=CD(正方形各边都相等),∴DF=A1D/2(等量代换).∴∠DA1F=300 (在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300).又∵AD∥EF,∴∠A1DA=∠DA1F=300 (两直线平行,内错角相等).∴∠ADG=∠A1DA/2=150(角平分线意义).●●300 要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°∠A=60°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.ACB┓请你分一分1、在△ABC中,AB=AC,∠C=30°,DA⊥BA于A,
BC=15,求AD的长 解:∵AB=AC∴∠B=∠C=30°∵DA⊥BA∴AD=1/2BD , ∠ADB=60°∵ ∠ADB=60° ∠C=30°∴∠DAC= ∠C=30°∴AD=DC=1/2BD∵BC=15∴AD=DC=5五、延伸拓展回味无穷等边三角形的判定:
定义:有三边相等的三角形是等边三角形.
定理:有一个角是600的等腰三角形是等边三角形.
定理:三个角都相等的三角形是等边三角形.
特殊的直角三角形的性质:
定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.等边三角形的性质:
三边相等,三个角都是600,”三线合一”,三条对称轴.结束寄语严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则. 再 见!教科书P83习题13.3
第12、13、14题.布置作业
求证:AE=CD证明:∵ △ABC和△BDE都是等边三角形∴AB=BC,∠ABC=∠DBE=60°,BE=BD∴ △ABE≌△CBD∴AE=CD发散练习:第十三章 轴对称13.3.2等边三角形 问题 已知△ABC 中,∠A =60°,( ?????? ?).
请你在括号内补充一个条件,使△ABC 能成为等边三角
形.∠B =60°(或∠C =60°)
AB =BC、AC =BC、AB =BC =AC 创设情境,导入新知 思考2 这个特殊的直角三角形相比一般的直角三角形有什么不同之处,它有什么特殊性质?创设情境,导入新知 思考1 等边三角形是轴对称图形,若沿着其中一
条对称轴折叠,能产生什么特殊图形? 活动 用两个全等的含30°角的直角三角尺,你能
拼出怎样的三角形?能拼出等边三角形吗?请说说你的
理由. 活动操作,探索性质BC = AB. 活动操作,探索性质 问题 你能借助这个图形,找到含30°角的直角
△ABC 的直角边BC 与斜边AB 之间有什么数量关系吗? 证明∵△ABC与△ADC关于AC轴对称
∴AB=AD
∠BAD=2× 30°= 60°
∴△ABD是等边三角形
又∵AC⊥BD
∴BC=DC= BD= AB从中你能得到
什么结论? 思考 这个命题是真命题吗?请进行证明. 问题 请说一说你猜想的命题中,条件和结论分别是什么?并结合图形,用符号语言表述出来.活动操作,探索性质 猜想 在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半.证明:在△ABC 中,
∵ ∠C =90°,∠A =30°,
∴ ∠B =60°.
延长BC 到D,使BD =AB,
连接AD,
则△ABD 是等边三角形. 已知:如图,在Rt△ABC 中,∠C =90°,∠A =
30°. 求证:BC = AB.活动操作,探索性质∴ BC = BD = AB . 已知:如图,在Rt△ABC 中,∠C =90°,∠A =
30°. 求证:BC = AB. 追问:你还能用其他方
法证明吗? 活动操作,探索性质证明:由等边三角形的性质可知,
AC 也是BD 边上的中线,动手操作,探索性质另证:作∠BCE =60°,交AB于E,连接CE, 则∠ACE =90°-60°=30°.
在△ABC 中,
∵ ∠ACB=90°,∠A =30°,
∴ ∠B =60°.
在△BCE 中,
∵ ∠BCE=60°,∠B =60°,
∴ △BCE 是等边三角形.
∴ BC =BE =CE.动手操作,探索性质∴ BC =BE =AE = AB. 另证:
在△ACE 中,
∵ ∠A=30°,∠ACE =30°,
∴ △AEC是等腰三角形.
∴ CE =AE.
∴ BC =BE =CE =AE.符号语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°, 动手操作,探索性质 在直角三角形中,如果一个锐角等于30°,那么
它所对的直角边等于斜边的一半.∴ BC = AB. 定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.在Rt△ABC中
∵∠A=30°
∴AB=2BCABC300这又是一个判定两条线段成倍分关系的根据之一.5课堂练习 练习1 如图,在△ABC 中,∠C =90°,∠A =
30°,AB =10,则BC 的长为 .1课堂练习 练习2 如图,在△ABC 中,∠ACB =90°,CD 是
高,∠A =30°,AB =4.则BD = . 思考 图中BC、DE 分
别是哪个直角三角形的直角
边?它们所对的锐角分别是
多少度? 性质运用 例 如图是屋架设计图的一部分,点D 是斜梁AB
的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,
∠A =30°,立柱BC、DE 要多长?解:∵DE⊥AC, BC⊥AC, ∠A=30°
可得 BC= AB, DE= AD
∴BC= ×7.4=3.7m
又 AD= AB
∴DE= AD= ×3.7=1.85m
答:立柱BC的长是3.7m,DE的长是1.85m.这又是一个判定两条线段成倍分关系的根据之一.记住哟′解:过C作BA延长线的垂线CD,垂足为D
∵∠B=∠ACB=150(已知),
∴∠DAC=∠B+∠ACB= 150+150=300
(三角形的一个外角,等于和它不相邻的两内角的和).
∴CD= AC= ×2a=a
(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半).ACBD150150例2.已知:等腰三角形的底角为150,腰长为2a.
求:腰上的高.2a例3.已知:如图,在△ABC中,∠ACB=900,∠A=300,CD⊥AB于D.
求证:BD= AB.你能规范地写出证明过程吗?你的证题能力有所提高吗?ACBD反过来怎么样——逆向思维命题:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.是真命题吗?
如果是,请你证明它.ABC已知:如图,在△ABC中,∠ACB=900,BC= AB.
求证:∠A=300.反过来怎么样——逆向思维在△ABD中,∵∠ACB=900(已知),
∴AB=AD(线段垂直平分线上的点到线段两端的距离相等).
又∵BC=AB/2(已知),
BC=BD/2(作图),
∴AB=BD(等量代换).
∴AB=BD=AD(等式性质).
∴△ABD是等边三角形(等边三角形定义).
∴∠B=600(等边三角形定义).
∴∠A=300(直角三角形两锐角互余).300ABC证明:如图, 延长BC至D,使CD=BC,连接AD.几何的三种语言′这是一个通过线段之间的关系来判定一个角的具体度数(300)的根据之一.定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.在△ABC中
∵∠ACB=900,BC=AB/2(已知),
∴∠A=300(在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300).比一比:看 谁 算 的 快1.如图:在Rt△ABC中
∠A=300,AB+BC=12cm
则AB=_____cm82.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm, BD=___, BE=____4cm 2cm挑战自我:相信你一定能行2.如图:已知 在△ABC 中,∠A=300,C=900,BD平分∠ABC.
求证:AD=2DC1.如图,在△ABC中,∠C=900,∠B=150, DE是AB的中垂线,BE=5,
则AE=______,AC=_____成功者的摇篮1.如图(1):四边形ABCD是一张正方形纸片,E,F分别是AB,CD的中点,沿着过点D的折痕将A角翻折,使得A落在EF上(如图(2)), 折痕交AE于点G,那么∠ADG等于多少度?你能证明你的结论吗?DACBEF(1)(2)GA成功者的摇篮答:∠ADG等于150. 证明:∵DF=DC/2(中点定义),A1D=AD=CD(正方形各边都相等),∴DF=A1D/2(等量代换).∴∠DA1F=300 (在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300).又∵AD∥EF,∴∠A1DA=∠DA1F=300 (两直线平行,内错角相等).∴∠ADG=∠A1DA/2=150(角平分线意义).●●300 要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°∠A=60°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.ACB┓请你分一分1、在△ABC中,AB=AC,∠C=30°,DA⊥BA于A,
BC=15,求AD的长 解:∵AB=AC∴∠B=∠C=30°∵DA⊥BA∴AD=1/2BD , ∠ADB=60°∵ ∠ADB=60° ∠C=30°∴∠DAC= ∠C=30°∴AD=DC=1/2BD∵BC=15∴AD=DC=5五、延伸拓展回味无穷等边三角形的判定:
定义:有三边相等的三角形是等边三角形.
定理:有一个角是600的等腰三角形是等边三角形.
定理:三个角都相等的三角形是等边三角形.
特殊的直角三角形的性质:
定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.等边三角形的性质:
三边相等,三个角都是600,”三线合一”,三条对称轴.结束寄语严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则. 再 见!教科书P83习题13.3
第12、13、14题.布置作业
