反比例函数的应用.[上学期]

课件18张PPT。5.3反比例函数的应用教学目标:
1.知识与技能
(1)利用反比例函数解决实际问题及有关反比例函数的综合题.
(2)建立反比例函数模型及综合运用有关知识解决与反比例函数有关的综合问题.
2.过程与方法
经历分析实际问题中变量之间的关系,建立反比例函数模型,进而解决问题的过程.
3.情感、态度与价值观
体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力.
教学重点与难点
1.重点:利用反比例函数解决实际问题及有关反比例函数的综合问题.
2.难点:建立反比例函数模型及综合运用有关知识解决与反比例函数有关的综合问题.挑战记忆:反比例函数图象有哪些性质?反比例函数 是由两支曲线组成,当K>0时,两支曲线分别位于第一、三象限内，在每一象限内，y随x的增大而减少；当K<0时,两支曲线分别位于第二、四象限内,在每一象限内,y随x的增大而增大. 某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化?探究: 如果人和木板对湿地地面的压力合计600N,那么(1)用含S的代数式表示P,P是S的反比例函数吗?为什么?P是S的反比例函数.解:探究:(2)当木板面积为0.2m2时,压强是多少?解:当S=0.2m2时,P=600/0.2=3000(Pa) (3)如果要求压强不超过6000Pa,木板面积至少要多大? 解:当P≤6000时,S≥600/6000=0.1(m2)
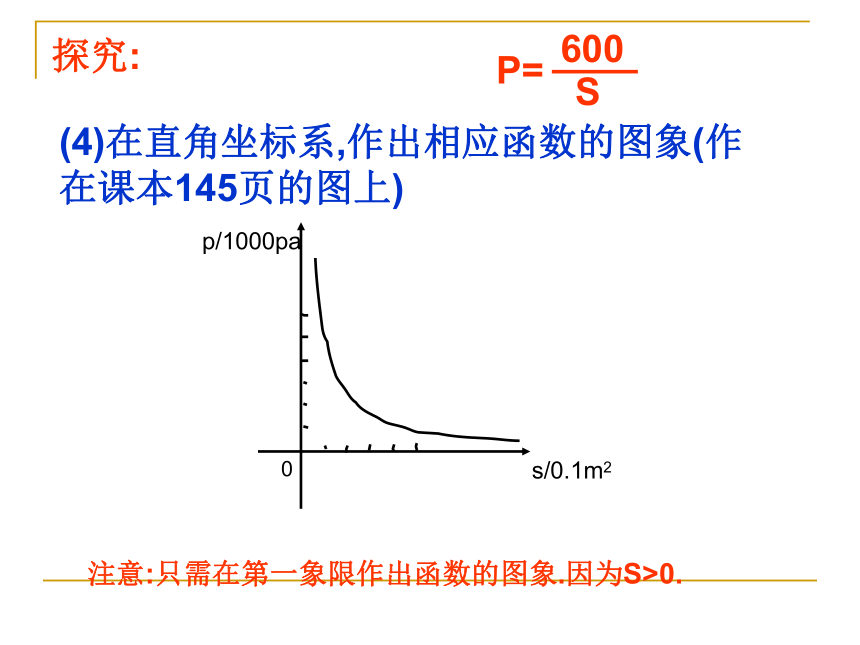
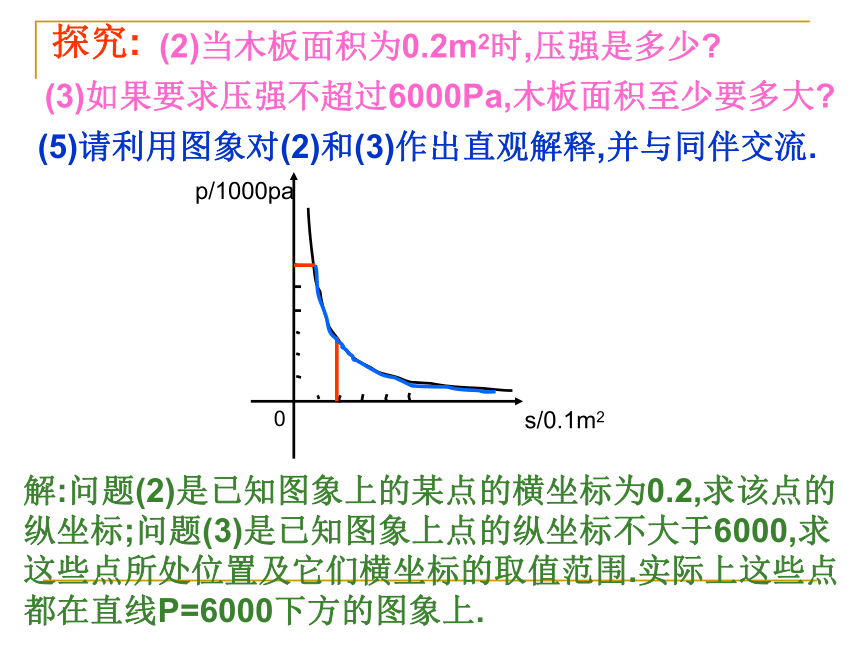
所以木板面积至少要0.1m2.(4)在直角坐标系,作出相应函数的图象(作在课本145页的图上)注意:只需在第一象限作出函数的图象.因为S>0.探究:(5)请利用图象对(2)和(3)作出直观解释,并与同伴交流.解:问题(2)是已知图象上的某点的横坐标为0.2,求该点的纵坐标;问题(3)是已知图象上点的纵坐标不大于6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线P=6000下方的图象上.(2)当木板面积为0.2m2时,压强是多少?(3)如果要求压强不超过6000Pa,木板面积至少要多大?探究:做一做(见146页第1题)(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?1.蓄电池的电压为定值.使用此电源时,电流I(A)与电阻R(?)之间的函数关系如图所示:(2)完成下表,并回答问题:如果以此蓄电池为电源的用电器电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?(1)分别写出这两个函数的表达式;
(2)你能求出点B的坐标吗?你是怎样求的?与同伴交流?2.如图,正比例函数y=k1x的图象与反比例函数
y=k2/x的图象交于A,B两点,其中点A的坐标为所以所求的函数表达式为:y=2x,和y=6/x.随堂练习:课本147页.1.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(1)蓄水池的容积是多少?解:蓄水池的容积为:8×6=48(m3).(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?答:此时所需时间t(h)将减少.(3)写出t与Q之间的函数关系式;随堂练习:课本147页.1.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?解:当t=5h时,Q=48/5=9.6m3.所以每时的排水量至少为9.6m3.(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空?解:当Q=12(m3)时,t=48/12=4(h).所以最少需4h可将满池水全部排空.(6)画出函数图象,根据图象请对问题(4)和(5)作出直观解释,并和同伴交流.超越自我:CDCDyxAOBMN本课小结:
.通过本节课的学习,你有哪些收获?利用反比例函数解决实际问题的关键:建立反比例函数模型.布置作业:课本148页习题5.4祝同学们学习进步！
再见