2.3一元二次不等式及其解法 讲义-2022-2023学年高一上学期数学人教A版(2019 )必修第一册(无答案)
文档属性
| 名称 | 2.3一元二次不等式及其解法 讲义-2022-2023学年高一上学期数学人教A版(2019 )必修第一册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 511.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 04:23:50 | ||
图片预览



文档简介
数学学科学生讲义
学生姓名: 年级: 科目:数学 学科教师:
课题 2.3一元二次不等式及其解法
授课类型 基础知识 经典例题 课堂练习 考试真题
教学目标
教学重难点
授课日期及时段
教学内容
知识清单 二次函数、一元二次方程与一元二次不等式(根据开口方向和) 的图像方程的解无解的解或的解无解无解的图像 方程的解无解的解的解或
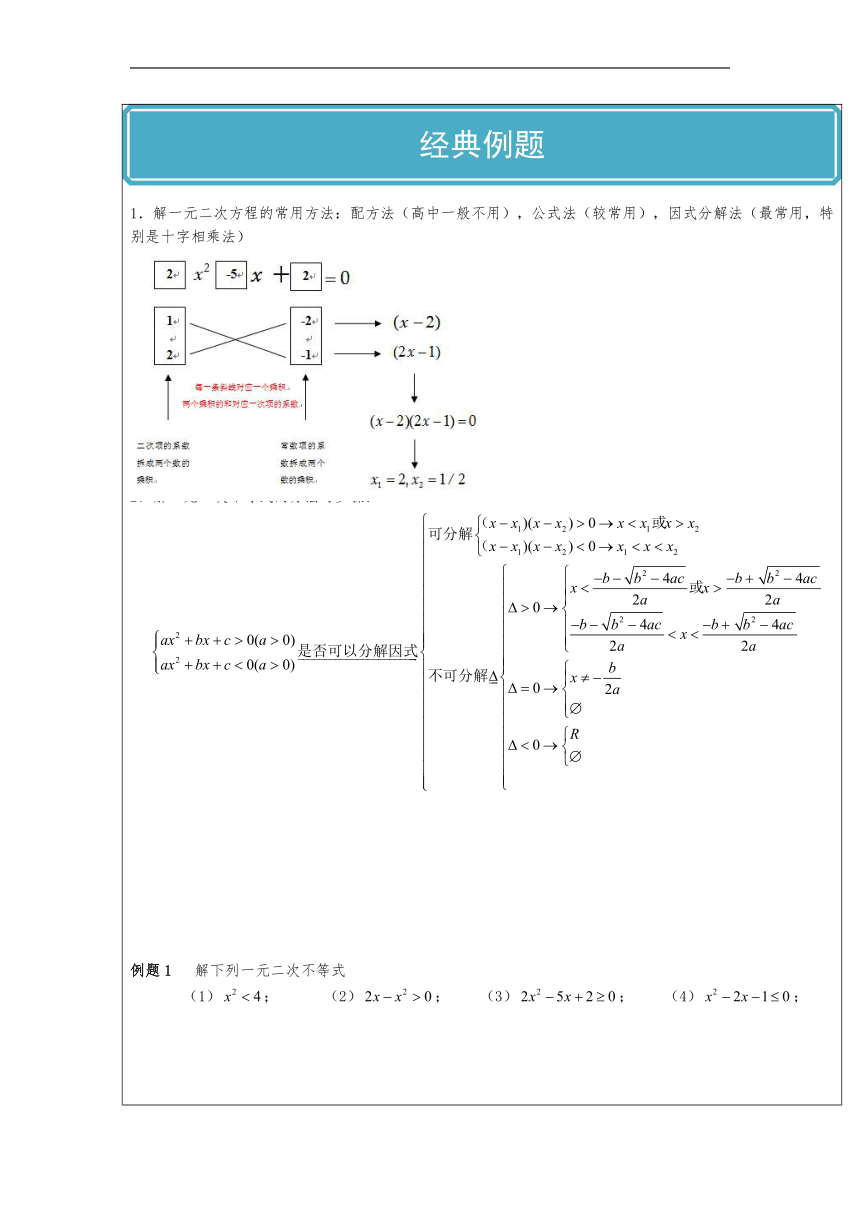
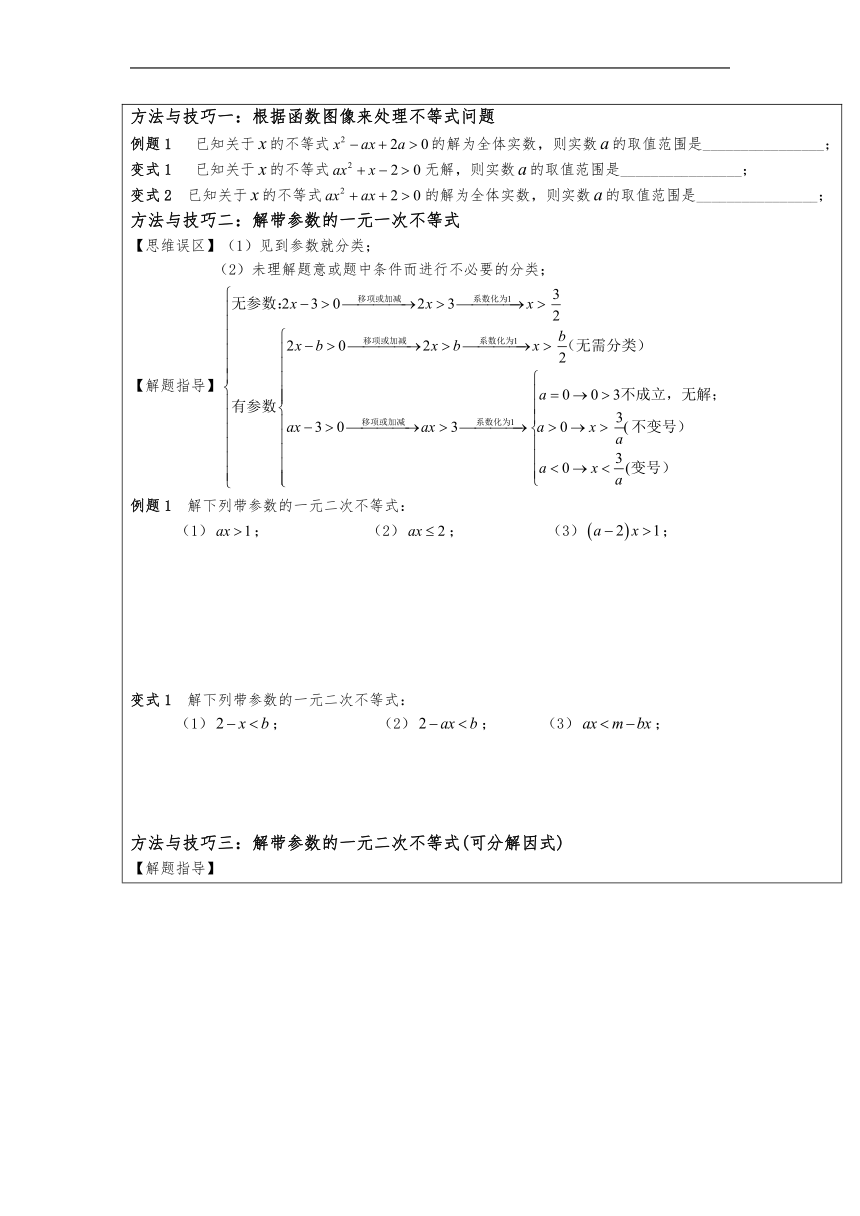
重要知识点讲解 知识点一:解一元二次不等式 【解题指导】 1.解一元二次方程的常用方法:配方法(高中一般不用),公式法(较常用),因式分解法(最常用,特别是十字相乘法) 2.解一元二次不等式的方法与步骤: 例题1 解下列一元二次不等式 (1); (2); (3); (4); (5);(6); (7); (8); 变式1解下列一元二次不等式 (1); (2); 例题2不等式的解集是____________; 变式2不等式的解集为____________; 变式3不等式的解集为____________; 变式4不等式的解集为____________; 知识点二:解高次不等式 【解题指导】解高次不等式一般用“序轴法(穿针引线)来解决;主要步骤是: (1)将最高次项的系数化为正数;(2)按照“从右到左,从上到下,奇次穿过,偶次不穿过”的思路作出图像;(3)由图像直接写出不等式的解; 例题1解下列高次不等式 (1); (2); (3); (4); 知识点三:解分式不等式 【解题指导】分式不等式要先化为整式不等式,然后再按照整式不等式的方法来解答; 例题1 解下列分式不等式 (1); (2); (3); (4); (5); 例题2解下列分式不等式 (1); (2); (3); (4); (5); (6); (7); 变式1 解下列分式不等式 (1); (2); 重要方法与技巧讲解 方法与技巧一:根据函数图像来处理不等式问题 例题1 已知关于的不等式的解为全体实数,则实数的取值范围是________________; 变式1 已知关于的不等式无解,则实数的取值范围是________________; 变式2 已知关于的不等式的解为全体实数,则实数的取值范围是________________; 方法与技巧二:解带参数的一元一次不等式 【思维误区】(1)见到参数就分类; (2)未理解题意或题中条件而进行不必要的分类; 【解题指导】 例题1 解下列带参数的一元二次不等式: (1); (2); (3); 变式1 解下列带参数的一元二次不等式: (1); (2); (3); 方法与技巧三:解带参数的一元二次不等式(可分解因式) 【解题指导】 例题1 ; 变式1 ; 方法与技巧四:解带参数的一元二次不等式(不可分解因式) 例题1 ; 变式1 ; 例题2 ; 变式2 ; 方法与技巧五:存在问题与恒成立问题 例题1 已知二次函数,且,是否存在常数使得连续不等式对一切实数恒成立?并求出的值; 变式1 已知是偶函数,当时,,若当时,恒成立,则的最小值为( ) A. 1 B. C. D. 变式2 不等式对任意实数恒成立,则实数的取值范围为( ) A. B. C. D. 例题2 已知,不等式有解,则的取值范围为________; 变式3 若关于x的不等式在[1,2]上有解,求实数a的取值范围。 随堂练习 1.解下列不等式:(1) (2) (4) 2.解下列不等式:(1) (2) 3.解连续不等式:; 4.解关于x的不等式; 5.解下列不等式:(1) (2) 6.解下列不等式:(1) (2) 7.设函数,对任意,恒成立,则实数m的取值范围是 ; 8.在实数上定义运算:,若不等式对任意实数x恒成立,则实数a的取值范围是 ; 9.某农贸公司按每担200元的价格收购某农产品,并按每100元纳税10元(又称征税率为10个百分点)进行纳税。计划科收购a万担,政府为了鼓励收购公司多收购这种农产品,决定将征稅率降低个百分点,预测收购量可增加2x个百分点。 (1)写出税收y(万元)与x的函数关系式 (2)要使次项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围。 A.基础过关 一、选择题 1. 不等式的解集为( ) A. B. C. D. 2.不等式的解集是( ) A. B. C. D. 3.不等式的解集为( ) A. B. C. D. 4 .不等式的解集是( ) A. B. C. D. 5. 不等式的解集是,则m,n的值分别是( ) A. 2,12 B. 2,-2 C. 2,-12 D. -2,-12 6. 已知不等式的解集为空集,则a的取值范围是( ) A. B. C. D. 7. 已知关于x的不等式对任意恒成立,则有( ) A. B. C. D. 二、填空题 8. 二次函数的部分对应值如下表: x-3-2-101234y60-4-6-6-406
则不等式的解集是 ; 9.不等式的解集为 ; 10.不等式的解集为 ; 11.不等式的解集是 ; 12.设,则关于x的不等式的解集是 ; 13. 若函数的值域为R,则实数a的取值范围是 ; 三、解答题 14.设,解关于x的不等式; 15.解关于x的不等式:; 16.某地区上年度电价为0.8元/千瓦时,年用电量为a千瓦时,本年度计划将电价降低到0.55元/千瓦时至0.75元/千瓦时之间,而用户期望电价为0.4元/千瓦时。经测算,下周电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k)。该地区电力的成本家为0.3元/千瓦时。 (1)写出本年度电价下调后,电力部门的收益为y与实际电价x的函数关系式; (2)设,当电价最低定位多少时仍可保证电力部门的收益比上年度至少增长20%(收益=实际用电量(实际电价-成本价))? 三年模拟 一、选择题 1.(★☆☆)不等式的解集为( ) A. B. C. D. 2.(★☆☆)若,,则( ) A. B. C. D. 3.(★☆☆)不等式的解集为( ) A. B. C. D. 4.(★★☆)在R上定义运算“”:,则满足的实数x的取值范围为( ) A. (0,2) B. (-2,1) C. D.(-1,2) 5.(★★★)设函数则不等式的解集是( ) A. B. C. D. 6.(★★★)已知二次函数,且函数在(-2,-1)上恰有一个零点,则不等式的解集为( ) A. B. C. (-1,0) D. (0,1) 二、填空题 7.(★☆☆)已知全集,Z是整数集,集合,则中元素的个数为 。 8.(★☆☆)已知关于x的不等式的解集为,则不等式的解集为 。 9.(★★☆)不等式的解集是 。 10.(★★★)已知函数,则满足不等式的x的取值范围是 。 三、解答题 11.(★★☆)设函数, (1)不等式的解集为(1-,2),求a的值; (2)在(1)的条件下,试求不等式的解集。 12. (★★☆)解下列不等式: (1) (2)
学生姓名: 年级: 科目:数学 学科教师:
课题 2.3一元二次不等式及其解法
授课类型 基础知识 经典例题 课堂练习 考试真题
教学目标
教学重难点
授课日期及时段
教学内容
知识清单 二次函数、一元二次方程与一元二次不等式(根据开口方向和) 的图像方程的解无解的解或的解无解无解的图像 方程的解无解的解的解或
重要知识点讲解 知识点一:解一元二次不等式 【解题指导】 1.解一元二次方程的常用方法:配方法(高中一般不用),公式法(较常用),因式分解法(最常用,特别是十字相乘法) 2.解一元二次不等式的方法与步骤: 例题1 解下列一元二次不等式 (1); (2); (3); (4); (5);(6); (7); (8); 变式1解下列一元二次不等式 (1); (2); 例题2不等式的解集是____________; 变式2不等式的解集为____________; 变式3不等式的解集为____________; 变式4不等式的解集为____________; 知识点二:解高次不等式 【解题指导】解高次不等式一般用“序轴法(穿针引线)来解决;主要步骤是: (1)将最高次项的系数化为正数;(2)按照“从右到左,从上到下,奇次穿过,偶次不穿过”的思路作出图像;(3)由图像直接写出不等式的解; 例题1解下列高次不等式 (1); (2); (3); (4); 知识点三:解分式不等式 【解题指导】分式不等式要先化为整式不等式,然后再按照整式不等式的方法来解答; 例题1 解下列分式不等式 (1); (2); (3); (4); (5); 例题2解下列分式不等式 (1); (2); (3); (4); (5); (6); (7); 变式1 解下列分式不等式 (1); (2); 重要方法与技巧讲解 方法与技巧一:根据函数图像来处理不等式问题 例题1 已知关于的不等式的解为全体实数,则实数的取值范围是________________; 变式1 已知关于的不等式无解,则实数的取值范围是________________; 变式2 已知关于的不等式的解为全体实数,则实数的取值范围是________________; 方法与技巧二:解带参数的一元一次不等式 【思维误区】(1)见到参数就分类; (2)未理解题意或题中条件而进行不必要的分类; 【解题指导】 例题1 解下列带参数的一元二次不等式: (1); (2); (3); 变式1 解下列带参数的一元二次不等式: (1); (2); (3); 方法与技巧三:解带参数的一元二次不等式(可分解因式) 【解题指导】 例题1 ; 变式1 ; 方法与技巧四:解带参数的一元二次不等式(不可分解因式) 例题1 ; 变式1 ; 例题2 ; 变式2 ; 方法与技巧五:存在问题与恒成立问题 例题1 已知二次函数,且,是否存在常数使得连续不等式对一切实数恒成立?并求出的值; 变式1 已知是偶函数,当时,,若当时,恒成立,则的最小值为( ) A. 1 B. C. D. 变式2 不等式对任意实数恒成立,则实数的取值范围为( ) A. B. C. D. 例题2 已知,不等式有解,则的取值范围为________; 变式3 若关于x的不等式在[1,2]上有解,求实数a的取值范围。 随堂练习 1.解下列不等式:(1) (2) (4) 2.解下列不等式:(1) (2) 3.解连续不等式:; 4.解关于x的不等式; 5.解下列不等式:(1) (2) 6.解下列不等式:(1) (2) 7.设函数,对任意,恒成立,则实数m的取值范围是 ; 8.在实数上定义运算:,若不等式对任意实数x恒成立,则实数a的取值范围是 ; 9.某农贸公司按每担200元的价格收购某农产品,并按每100元纳税10元(又称征税率为10个百分点)进行纳税。计划科收购a万担,政府为了鼓励收购公司多收购这种农产品,决定将征稅率降低个百分点,预测收购量可增加2x个百分点。 (1)写出税收y(万元)与x的函数关系式 (2)要使次项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围。 A.基础过关 一、选择题 1. 不等式的解集为( ) A. B. C. D. 2.不等式的解集是( ) A. B. C. D. 3.不等式的解集为( ) A. B. C. D. 4 .不等式的解集是( ) A. B. C. D. 5. 不等式的解集是,则m,n的值分别是( ) A. 2,12 B. 2,-2 C. 2,-12 D. -2,-12 6. 已知不等式的解集为空集,则a的取值范围是( ) A. B. C. D. 7. 已知关于x的不等式对任意恒成立,则有( ) A. B. C. D. 二、填空题 8. 二次函数的部分对应值如下表: x-3-2-101234y60-4-6-6-406
则不等式的解集是 ; 9.不等式的解集为 ; 10.不等式的解集为 ; 11.不等式的解集是 ; 12.设,则关于x的不等式的解集是 ; 13. 若函数的值域为R,则实数a的取值范围是 ; 三、解答题 14.设,解关于x的不等式; 15.解关于x的不等式:; 16.某地区上年度电价为0.8元/千瓦时,年用电量为a千瓦时,本年度计划将电价降低到0.55元/千瓦时至0.75元/千瓦时之间,而用户期望电价为0.4元/千瓦时。经测算,下周电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k)。该地区电力的成本家为0.3元/千瓦时。 (1)写出本年度电价下调后,电力部门的收益为y与实际电价x的函数关系式; (2)设,当电价最低定位多少时仍可保证电力部门的收益比上年度至少增长20%(收益=实际用电量(实际电价-成本价))? 三年模拟 一、选择题 1.(★☆☆)不等式的解集为( ) A. B. C. D. 2.(★☆☆)若,,则( ) A. B. C. D. 3.(★☆☆)不等式的解集为( ) A. B. C. D. 4.(★★☆)在R上定义运算“”:,则满足的实数x的取值范围为( ) A. (0,2) B. (-2,1) C. D.(-1,2) 5.(★★★)设函数则不等式的解集是( ) A. B. C. D. 6.(★★★)已知二次函数,且函数在(-2,-1)上恰有一个零点,则不等式的解集为( ) A. B. C. (-1,0) D. (0,1) 二、填空题 7.(★☆☆)已知全集,Z是整数集,集合,则中元素的个数为 。 8.(★☆☆)已知关于x的不等式的解集为,则不等式的解集为 。 9.(★★☆)不等式的解集是 。 10.(★★★)已知函数,则满足不等式的x的取值范围是 。 三、解答题 11.(★★☆)设函数, (1)不等式的解集为(1-,2),求a的值; (2)在(1)的条件下,试求不等式的解集。 12. (★★☆)解下列不等式: (1) (2)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
