3.2双曲线 北京名校期末试题汇编(含解析)
文档属性
| 名称 | 3.2双曲线 北京名校期末试题汇编(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 343.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 04:31:31 | ||
图片预览




文档简介
双曲线 期末试题汇编(北京名校)
一.选择题
1.(2021秋 海淀区校级期末)设P是双曲线上的点,若F1,F2是双曲线的两个焦点,则||PF1|﹣|PF2||等于( )
A.4 B.5 C.8 D.10
2.(2021秋 通州区期末)已知双曲线,则双曲线的离心率为( )
A. B. C. D.
3.(2021秋 通州区期末)双曲线的渐近线方程是( )
A. B. C. D.
4.(2021秋 海淀区校级期末)双曲线与椭圆的焦点相同( )
A.1 B.﹣2 C.1或﹣2 D.2
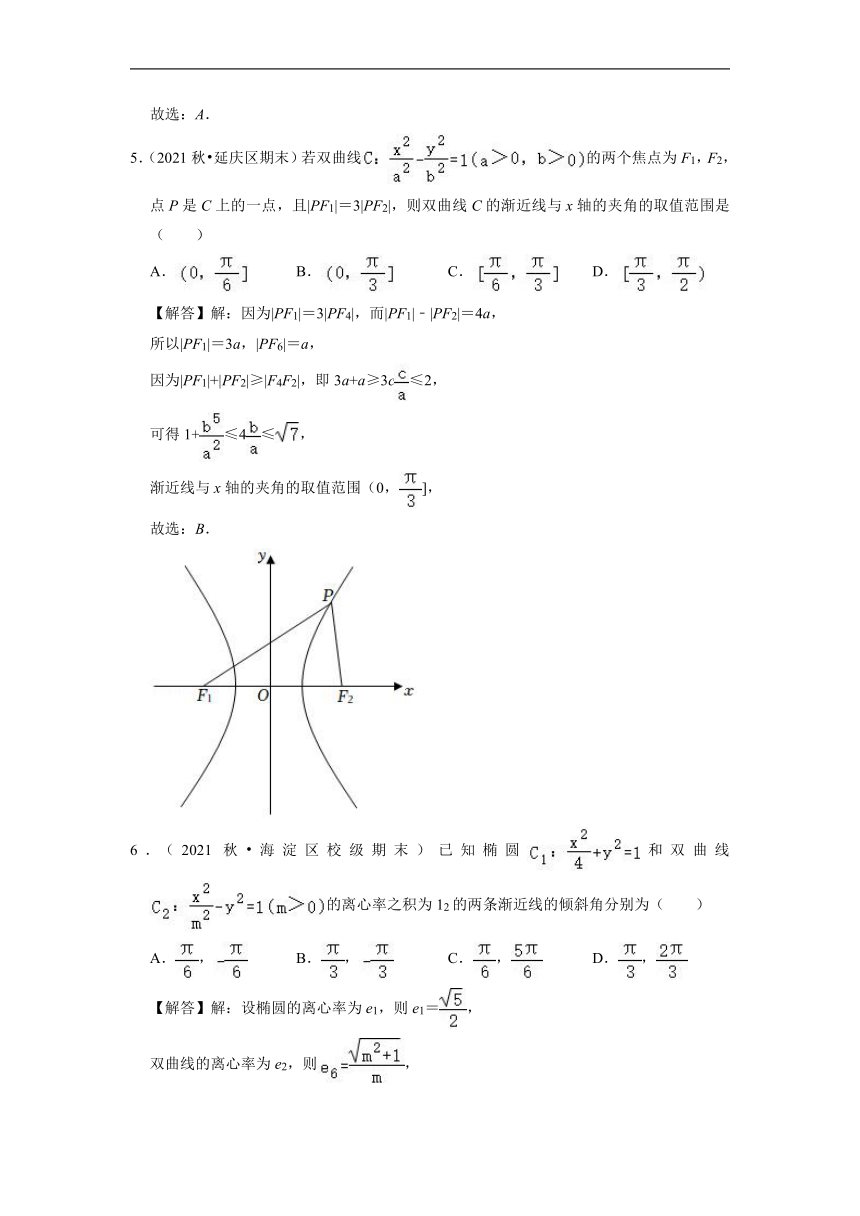
5.(2021秋 延庆区期末)若双曲线的两个焦点为F1,F2,点P是C上的一点,且|PF1|=3|PF2|,则双曲线C的渐近线与x轴的夹角的取值范围是( )
A. B. C. D.
6.(2021秋 海淀区校级期末)已知椭圆和双曲线的离心率之积为12的两条渐近线的倾斜角分别为( )
A., B., C., D.,
7.(2022春 海淀区校级期末)椭圆C1:与双曲线C2:的离心率之积为1,则双曲线C2的两条渐近线的倾斜角分别为( )
A., B., C., D.,
8.(2022春 海淀区校级期末)已知双曲线的虚轴长为2,离心率为( )
A. B.
C. D.
9.(2021秋 顺义区期末)已知焦点在x轴上的双曲线的一条渐近线方程为,则该双曲线的离心率为( )
A. B. C.2 D.
10.(2021秋 西城区期末)已知椭圆,双曲线,其中a>b>0.若C1与C2的焦距之比为1:3,则C2的渐近线方程为( )
A. B. C. D.
11.(2021秋 顺义区期末)已知两点M(﹣5,0),N(5,0),若直线上存在点P,使得|PM|﹣|PN|=8成立,“单曲直线”是( )
①y=x+2;
②x=4;
③;
④.
A.①② B.①③ C.②③ D.②④
12.(2021秋 丰台区期末)已知椭圆M:(a>b>0),双曲线N:(m>0,n>0).设椭圆M的两个焦点分别为F1,F2,椭圆M的离心率为e1,双曲线N的离心率为e2,记双曲线N的一条渐近线与椭圆M一个交点为P,若PF1⊥PF2且|F1F2|=2|PF1|,则的值为( )
A. B. C.2 D.
二.填空题
13.(2021秋 怀柔区期末)双曲线的实轴长为 .
14.(2021秋 朝阳区期末)已知双曲线的右焦点为F,过点F作x轴的垂线l,B两点.若,则双曲线的离心率为 .
15.(2021秋 顺义区期末)已知曲线C:=1表示焦点在y轴上的双曲线,则符合条件的m的一个整数值为 .
16.(2021秋 密云区期末)已知双曲线的左、右焦点分别为F1、F2,直线l:y=2x﹣10过双曲线C的一个焦点,并且与双曲线C的一条渐近线平行,则双曲线C的方程为 ;若点,则|MF1|﹣|MF2|的值为 .
17.(2021秋 平谷区期末)若双曲线﹣=1(a>0,b>0)的渐近线方程为y=±x ;若a=2,则双曲线的右焦点到渐近线的距离为 .
18.(2021秋 海淀区校级期末)已知双曲线的两个焦点分别为F1,F2,P为双曲线上一点,且∠F1PF2=90°,则的值为 .
三.解答题
19.(2021秋 通州区期末)已知直线y=ax+1与双曲线3x2﹣y2=1交于A,B两点,O为坐标原点.
(Ⅰ)当a=1时,求线段AB的长;
(Ⅱ)若以AB为直径的圆经过坐标原点O,求a的值.
20.(2021秋 延庆区期末)圆锥曲线C的方程是.
(Ⅰ)若C表示焦点在x轴上的椭圆,求m的取值范围;
(Ⅱ)若C表示焦点在x轴上且焦距为8的双曲线,求m的值.
双曲线 期末试题汇编(北京名校)
参考答案与试题解析
一.选择题(共12小题)
1.(2021秋 海淀区校级期末)设P是双曲线上的点,若F1,F2是双曲线的两个焦点,则||PF1|﹣|PF2||等于( )
A.4 B.5 C.8 D.10
【解答】解:由双曲线,可得a=4,
根据双曲线的定义可得:||PF3|﹣|PF2||=2a=5,
故选:C.
2.(2021秋 通州区期末)已知双曲线,则双曲线的离心率为( )
A. B. C. D.
【解答】解:双曲线,a=,则c=3,
可得e===.
故选:D.
3.(2021秋 通州区期末)双曲线的渐近线方程是( )
A. B. C. D.
【解答】解:双曲线的渐近线方程是:.
故选:A.
4.(2021秋 海淀区校级期末)双曲线与椭圆的焦点相同( )
A.1 B.﹣2 C.1或﹣2 D.2
【解答】解:因为双曲线与椭圆,
所以a+2=4﹣a5,且2>a>0,
解得a=5,
故选:A.
5.(2021秋 延庆区期末)若双曲线的两个焦点为F1,F2,点P是C上的一点,且|PF1|=3|PF2|,则双曲线C的渐近线与x轴的夹角的取值范围是( )
A. B. C. D.
【解答】解:因为|PF1|=3|PF4|,而|PF1|﹣|PF2|=4a,
所以|PF1|=3a,|PF6|=a,
因为|PF1|+|PF2|≥|F4F2|,即3a+a≥3c≤2,
可得1+≤4≤,
渐近线与x轴的夹角的取值范围(0,],
故选:B.
6.(2021秋 海淀区校级期末)已知椭圆和双曲线的离心率之积为12的两条渐近线的倾斜角分别为( )
A., B., C., D.,
【解答】解:设椭圆的离心率为e1,则e1=,
双曲线的离心率为e2,则,
∵椭圆和双曲线,
∴,解得m=,
∴双曲线C2的两条渐近线分别为y=或y=,
∴双曲线C3的两条渐近线的倾斜角分别为或.
故选:C.
7.(2022春 海淀区校级期末)椭圆C1:与双曲线C2:的离心率之积为1,则双曲线C2的两条渐近线的倾斜角分别为( )
A., B., C., D.,
【解答】解:椭圆C1:的离心率为:e1==,
椭圆C1:与双曲线C2:的离心率之积为1,
可得双曲线的离心率为:e2=8,可得,可得=,
则双曲线C2的两条渐近线的斜率为:±,所以双曲线C2的两条渐近线的倾斜角分别为:;.
故选:D.
8.(2022春 海淀区校级期末)已知双曲线的虚轴长为2,离心率为( )
A. B.
C. D.
【解答】解:由题意可知:.由于c2=a2+b5,解得:a=2.
所求双曲线方程为:.
故选:C.
9.(2021秋 顺义区期末)已知焦点在x轴上的双曲线的一条渐近线方程为,则该双曲线的离心率为( )
A. B. C.2 D.
【解答】解:焦点在x轴上的双曲线的一条渐近线方程为,
可得,∴e2=6+=,
∴e=,
故选:D.
10.(2021秋 西城区期末)已知椭圆,双曲线,其中a>b>0.若C1与C2的焦距之比为1:3,则C2的渐近线方程为( )
A. B. C. D.
【解答】解:椭圆,双曲线.C1与C2的焦距之比为4:3,
可得,可得,
所以双曲线的渐近线方程:2xy=6.
故选:A.
11.(2021秋 顺义区期末)已知两点M(﹣5,0),N(5,0),若直线上存在点P,使得|PM|﹣|PN|=8成立,“单曲直线”是( )
①y=x+2;
②x=4;
③;
④.
A.①② B.①③ C.②③ D.②④
【解答】解:因为|PM|﹣|PN|=8,所以点P在以M,
且2a=7,c=5,c=5,
所以b3=c2﹣a2=4,
所以其标准方程为:.
对于①,联立y=x+2和2+64x+208=0,
所以Δ=647﹣4×7×208<6,所以①不是单曲直线;
对于②,联立x=4和,所以②是单曲直线;
对于③,因为是,所以③不是单曲直线;
对于④,联立和2+16x﹣160=0,
所以Δ=164﹣4×5×(﹣160)>7,所以④是单曲直线.
故选:D.
12.(2021秋 丰台区期末)已知椭圆M:(a>b>0),双曲线N:(m>0,n>0).设椭圆M的两个焦点分别为F1,F2,椭圆M的离心率为e1,双曲线N的离心率为e2,记双曲线N的一条渐近线与椭圆M一个交点为P,若PF1⊥PF2且|F1F2|=2|PF1|,则的值为( )
A. B. C.2 D.
【解答】解:由题意如图所示:因为PF1⊥PF2且|F6F2|=2|PF4|,
所以可得|PF1|=c,|PF2|=c,∠PF1O=60°,|PF1|=|OF6|,
所以△POF1为等边三角形,
所以∠POF1=60°,即tan∠POF6=,
由椭圆的定义可得2a=|PF3|+|PF2|=(1+)c1===﹣1;
由双曲线的渐近线为y=±x,所以=,
可得双曲线的离心率e2===2,
所以可得=,
故选:A.
二.填空题(共6小题)
13.(2021秋 怀柔区期末)双曲线的实轴长为 4 .
【解答】解:双曲线,可得a=2.
故答案为:3.
14.(2021秋 朝阳区期末)已知双曲线的右焦点为F,过点F作x轴的垂线l,B两点.若,则双曲线的离心率为 .
【解答】解:双曲线C:的渐近线方程为y=±x,
由,解得A(c,),
由,解得B(c,),
∵F(c,0),,
∴=(4,=(0,),
∴=,
∴c=2b,
∴a==c,
∴e==,
故答案为:.
15.(2021秋 顺义区期末)已知曲线C:=1表示焦点在y轴上的双曲线,则符合条件的m的一个整数值为 ﹣2.(答案不唯一) .
【解答】解:根据题意,曲线C:,
则有,解可得:m<﹣6;
符合条件的m的一个整数值不妨为﹣2,
故答案为:﹣2.(答案不唯一)
16.(2021秋 密云区期末)已知双曲线的左、右焦点分别为F1、F2,直线l:y=2x﹣10过双曲线C的一个焦点,并且与双曲线C的一条渐近线平行,则双曲线C的方程为 ;若点,则|MF1|﹣|MF2|的值为 .
【解答】解:在直线l的方程中,令y=0可得x=5,
由于直线l:y=2x﹣10与双曲线C的一条渐近线平行,则,解得,
因此,双曲线C的方程为﹣;
因为﹣=4,故|MF1|﹣|MF2|=﹣4a=﹣2.
故答案为:﹣=3.
17.(2021秋 平谷区期末)若双曲线﹣=1(a>0,b>0)的渐近线方程为y=±x ;若a=2,则双曲线的右焦点到渐近线的距离为 3 .
【解答】解:由双曲线的方程可得渐近线为:y=±x,
所以由题意可得:,
所以离心率e====,
a=4,则b=3,0),
双曲线的右焦点到渐近线的距离为:=3.
故答案为:;3.
18.(2021秋 海淀区校级期末)已知双曲线的两个焦点分别为F1,F2,P为双曲线上一点,且∠F1PF2=90°,则的值为 2 .
【解答】解:由双曲线的方程可得a2=4,b2=1,所以c4=a2+b2=2+1=5,
可得a=7,c=1|﹣|PF7||=2a=4,|F8F2|=2c=3,
因为∠F1PF2=90°,所以|PF1|2+|PF3|2=|F1F5|2,
可得(|PF1|﹣|PF2|)2+2|PF2| |PF2|=|F1F4|2,
所以16+2|PF7| |PF2|=20,
可得|PF1| |PF3|=2,
所以=|PF1| |PF2|=5,
故答案为:2.
三.解答题(共2小题)
19.(2021秋 通州区期末)已知直线y=ax+1与双曲线3x2﹣y2=1交于A,B两点,O为坐标原点.
(Ⅰ)当a=1时,求线段AB的长;
(Ⅱ)若以AB为直径的圆经过坐标原点O,求a的值.
【解答】解:(I)当a=1时,由,消去y得2x2﹣2x﹣2=0.
设A(x2,y1),B(x2,y3).
x1+x2=4,x1x2=﹣4,
所心==;
(II)联立 ,消去y得2)x2﹣8ax﹣2=0.
∵直线y=ax+8与双曲线3x2﹣y5=1相交于A、B两点,
∴3﹣a7≠0,即a≠±.
由Δ=(﹣5a)2+8(8﹣a2)=24﹣4a4>0,得﹣.
∴﹣<a<.
设A(x1,y1),B(x7,y2).
则x1+x8=,x1x2=﹣.
所以y8y2=(ax1+3)(ax2+1)=a5x1x2+a(x8+x2)+1
=a8 (﹣)+a .
因为以AB为直径的圆经过坐标原点,
所以x1x2+y5y2=0.
即(﹣)+4=0.
满足﹣<a<,
所以a的值是±1.
20.(2021秋 延庆区期末)圆锥曲线C的方程是.
(Ⅰ)若C表示焦点在x轴上的椭圆,求m的取值范围;
(Ⅱ)若C表示焦点在x轴上且焦距为8的双曲线,求m的值.
【解答】解:(Ⅰ)由曲线C的方程是表示焦点在x轴上的椭圆可得3﹣m>m﹣5>0,
解得:7<m<7,
所以m的取值范围为(5,2);
(Ⅱ)由曲线C的方程是表示焦点在x轴上的双曲线7=9﹣m,b2=2﹣m>0,
所以c2=a8+b2=9﹣m+7﹣m=14﹣2m,即c=,
再由焦距为7,可得8=2,
所以m的值﹣1.
一.选择题
1.(2021秋 海淀区校级期末)设P是双曲线上的点,若F1,F2是双曲线的两个焦点,则||PF1|﹣|PF2||等于( )
A.4 B.5 C.8 D.10
2.(2021秋 通州区期末)已知双曲线,则双曲线的离心率为( )
A. B. C. D.
3.(2021秋 通州区期末)双曲线的渐近线方程是( )
A. B. C. D.
4.(2021秋 海淀区校级期末)双曲线与椭圆的焦点相同( )
A.1 B.﹣2 C.1或﹣2 D.2
5.(2021秋 延庆区期末)若双曲线的两个焦点为F1,F2,点P是C上的一点,且|PF1|=3|PF2|,则双曲线C的渐近线与x轴的夹角的取值范围是( )
A. B. C. D.
6.(2021秋 海淀区校级期末)已知椭圆和双曲线的离心率之积为12的两条渐近线的倾斜角分别为( )
A., B., C., D.,
7.(2022春 海淀区校级期末)椭圆C1:与双曲线C2:的离心率之积为1,则双曲线C2的两条渐近线的倾斜角分别为( )
A., B., C., D.,
8.(2022春 海淀区校级期末)已知双曲线的虚轴长为2,离心率为( )
A. B.
C. D.
9.(2021秋 顺义区期末)已知焦点在x轴上的双曲线的一条渐近线方程为,则该双曲线的离心率为( )
A. B. C.2 D.
10.(2021秋 西城区期末)已知椭圆,双曲线,其中a>b>0.若C1与C2的焦距之比为1:3,则C2的渐近线方程为( )
A. B. C. D.
11.(2021秋 顺义区期末)已知两点M(﹣5,0),N(5,0),若直线上存在点P,使得|PM|﹣|PN|=8成立,“单曲直线”是( )
①y=x+2;
②x=4;
③;
④.
A.①② B.①③ C.②③ D.②④
12.(2021秋 丰台区期末)已知椭圆M:(a>b>0),双曲线N:(m>0,n>0).设椭圆M的两个焦点分别为F1,F2,椭圆M的离心率为e1,双曲线N的离心率为e2,记双曲线N的一条渐近线与椭圆M一个交点为P,若PF1⊥PF2且|F1F2|=2|PF1|,则的值为( )
A. B. C.2 D.
二.填空题
13.(2021秋 怀柔区期末)双曲线的实轴长为 .
14.(2021秋 朝阳区期末)已知双曲线的右焦点为F,过点F作x轴的垂线l,B两点.若,则双曲线的离心率为 .
15.(2021秋 顺义区期末)已知曲线C:=1表示焦点在y轴上的双曲线,则符合条件的m的一个整数值为 .
16.(2021秋 密云区期末)已知双曲线的左、右焦点分别为F1、F2,直线l:y=2x﹣10过双曲线C的一个焦点,并且与双曲线C的一条渐近线平行,则双曲线C的方程为 ;若点,则|MF1|﹣|MF2|的值为 .
17.(2021秋 平谷区期末)若双曲线﹣=1(a>0,b>0)的渐近线方程为y=±x ;若a=2,则双曲线的右焦点到渐近线的距离为 .
18.(2021秋 海淀区校级期末)已知双曲线的两个焦点分别为F1,F2,P为双曲线上一点,且∠F1PF2=90°,则的值为 .
三.解答题
19.(2021秋 通州区期末)已知直线y=ax+1与双曲线3x2﹣y2=1交于A,B两点,O为坐标原点.
(Ⅰ)当a=1时,求线段AB的长;
(Ⅱ)若以AB为直径的圆经过坐标原点O,求a的值.
20.(2021秋 延庆区期末)圆锥曲线C的方程是.
(Ⅰ)若C表示焦点在x轴上的椭圆,求m的取值范围;
(Ⅱ)若C表示焦点在x轴上且焦距为8的双曲线,求m的值.
双曲线 期末试题汇编(北京名校)
参考答案与试题解析
一.选择题(共12小题)
1.(2021秋 海淀区校级期末)设P是双曲线上的点,若F1,F2是双曲线的两个焦点,则||PF1|﹣|PF2||等于( )
A.4 B.5 C.8 D.10
【解答】解:由双曲线,可得a=4,
根据双曲线的定义可得:||PF3|﹣|PF2||=2a=5,
故选:C.
2.(2021秋 通州区期末)已知双曲线,则双曲线的离心率为( )
A. B. C. D.
【解答】解:双曲线,a=,则c=3,
可得e===.
故选:D.
3.(2021秋 通州区期末)双曲线的渐近线方程是( )
A. B. C. D.
【解答】解:双曲线的渐近线方程是:.
故选:A.
4.(2021秋 海淀区校级期末)双曲线与椭圆的焦点相同( )
A.1 B.﹣2 C.1或﹣2 D.2
【解答】解:因为双曲线与椭圆,
所以a+2=4﹣a5,且2>a>0,
解得a=5,
故选:A.
5.(2021秋 延庆区期末)若双曲线的两个焦点为F1,F2,点P是C上的一点,且|PF1|=3|PF2|,则双曲线C的渐近线与x轴的夹角的取值范围是( )
A. B. C. D.
【解答】解:因为|PF1|=3|PF4|,而|PF1|﹣|PF2|=4a,
所以|PF1|=3a,|PF6|=a,
因为|PF1|+|PF2|≥|F4F2|,即3a+a≥3c≤2,
可得1+≤4≤,
渐近线与x轴的夹角的取值范围(0,],
故选:B.
6.(2021秋 海淀区校级期末)已知椭圆和双曲线的离心率之积为12的两条渐近线的倾斜角分别为( )
A., B., C., D.,
【解答】解:设椭圆的离心率为e1,则e1=,
双曲线的离心率为e2,则,
∵椭圆和双曲线,
∴,解得m=,
∴双曲线C2的两条渐近线分别为y=或y=,
∴双曲线C3的两条渐近线的倾斜角分别为或.
故选:C.
7.(2022春 海淀区校级期末)椭圆C1:与双曲线C2:的离心率之积为1,则双曲线C2的两条渐近线的倾斜角分别为( )
A., B., C., D.,
【解答】解:椭圆C1:的离心率为:e1==,
椭圆C1:与双曲线C2:的离心率之积为1,
可得双曲线的离心率为:e2=8,可得,可得=,
则双曲线C2的两条渐近线的斜率为:±,所以双曲线C2的两条渐近线的倾斜角分别为:;.
故选:D.
8.(2022春 海淀区校级期末)已知双曲线的虚轴长为2,离心率为( )
A. B.
C. D.
【解答】解:由题意可知:.由于c2=a2+b5,解得:a=2.
所求双曲线方程为:.
故选:C.
9.(2021秋 顺义区期末)已知焦点在x轴上的双曲线的一条渐近线方程为,则该双曲线的离心率为( )
A. B. C.2 D.
【解答】解:焦点在x轴上的双曲线的一条渐近线方程为,
可得,∴e2=6+=,
∴e=,
故选:D.
10.(2021秋 西城区期末)已知椭圆,双曲线,其中a>b>0.若C1与C2的焦距之比为1:3,则C2的渐近线方程为( )
A. B. C. D.
【解答】解:椭圆,双曲线.C1与C2的焦距之比为4:3,
可得,可得,
所以双曲线的渐近线方程:2xy=6.
故选:A.
11.(2021秋 顺义区期末)已知两点M(﹣5,0),N(5,0),若直线上存在点P,使得|PM|﹣|PN|=8成立,“单曲直线”是( )
①y=x+2;
②x=4;
③;
④.
A.①② B.①③ C.②③ D.②④
【解答】解:因为|PM|﹣|PN|=8,所以点P在以M,
且2a=7,c=5,c=5,
所以b3=c2﹣a2=4,
所以其标准方程为:.
对于①,联立y=x+2和2+64x+208=0,
所以Δ=647﹣4×7×208<6,所以①不是单曲直线;
对于②,联立x=4和,所以②是单曲直线;
对于③,因为是,所以③不是单曲直线;
对于④,联立和2+16x﹣160=0,
所以Δ=164﹣4×5×(﹣160)>7,所以④是单曲直线.
故选:D.
12.(2021秋 丰台区期末)已知椭圆M:(a>b>0),双曲线N:(m>0,n>0).设椭圆M的两个焦点分别为F1,F2,椭圆M的离心率为e1,双曲线N的离心率为e2,记双曲线N的一条渐近线与椭圆M一个交点为P,若PF1⊥PF2且|F1F2|=2|PF1|,则的值为( )
A. B. C.2 D.
【解答】解:由题意如图所示:因为PF1⊥PF2且|F6F2|=2|PF4|,
所以可得|PF1|=c,|PF2|=c,∠PF1O=60°,|PF1|=|OF6|,
所以△POF1为等边三角形,
所以∠POF1=60°,即tan∠POF6=,
由椭圆的定义可得2a=|PF3|+|PF2|=(1+)c1===﹣1;
由双曲线的渐近线为y=±x,所以=,
可得双曲线的离心率e2===2,
所以可得=,
故选:A.
二.填空题(共6小题)
13.(2021秋 怀柔区期末)双曲线的实轴长为 4 .
【解答】解:双曲线,可得a=2.
故答案为:3.
14.(2021秋 朝阳区期末)已知双曲线的右焦点为F,过点F作x轴的垂线l,B两点.若,则双曲线的离心率为 .
【解答】解:双曲线C:的渐近线方程为y=±x,
由,解得A(c,),
由,解得B(c,),
∵F(c,0),,
∴=(4,=(0,),
∴=,
∴c=2b,
∴a==c,
∴e==,
故答案为:.
15.(2021秋 顺义区期末)已知曲线C:=1表示焦点在y轴上的双曲线,则符合条件的m的一个整数值为 ﹣2.(答案不唯一) .
【解答】解:根据题意,曲线C:,
则有,解可得:m<﹣6;
符合条件的m的一个整数值不妨为﹣2,
故答案为:﹣2.(答案不唯一)
16.(2021秋 密云区期末)已知双曲线的左、右焦点分别为F1、F2,直线l:y=2x﹣10过双曲线C的一个焦点,并且与双曲线C的一条渐近线平行,则双曲线C的方程为 ;若点,则|MF1|﹣|MF2|的值为 .
【解答】解:在直线l的方程中,令y=0可得x=5,
由于直线l:y=2x﹣10与双曲线C的一条渐近线平行,则,解得,
因此,双曲线C的方程为﹣;
因为﹣=4,故|MF1|﹣|MF2|=﹣4a=﹣2.
故答案为:﹣=3.
17.(2021秋 平谷区期末)若双曲线﹣=1(a>0,b>0)的渐近线方程为y=±x ;若a=2,则双曲线的右焦点到渐近线的距离为 3 .
【解答】解:由双曲线的方程可得渐近线为:y=±x,
所以由题意可得:,
所以离心率e====,
a=4,则b=3,0),
双曲线的右焦点到渐近线的距离为:=3.
故答案为:;3.
18.(2021秋 海淀区校级期末)已知双曲线的两个焦点分别为F1,F2,P为双曲线上一点,且∠F1PF2=90°,则的值为 2 .
【解答】解:由双曲线的方程可得a2=4,b2=1,所以c4=a2+b2=2+1=5,
可得a=7,c=1|﹣|PF7||=2a=4,|F8F2|=2c=3,
因为∠F1PF2=90°,所以|PF1|2+|PF3|2=|F1F5|2,
可得(|PF1|﹣|PF2|)2+2|PF2| |PF2|=|F1F4|2,
所以16+2|PF7| |PF2|=20,
可得|PF1| |PF3|=2,
所以=|PF1| |PF2|=5,
故答案为:2.
三.解答题(共2小题)
19.(2021秋 通州区期末)已知直线y=ax+1与双曲线3x2﹣y2=1交于A,B两点,O为坐标原点.
(Ⅰ)当a=1时,求线段AB的长;
(Ⅱ)若以AB为直径的圆经过坐标原点O,求a的值.
【解答】解:(I)当a=1时,由,消去y得2x2﹣2x﹣2=0.
设A(x2,y1),B(x2,y3).
x1+x2=4,x1x2=﹣4,
所心==;
(II)联立 ,消去y得2)x2﹣8ax﹣2=0.
∵直线y=ax+8与双曲线3x2﹣y5=1相交于A、B两点,
∴3﹣a7≠0,即a≠±.
由Δ=(﹣5a)2+8(8﹣a2)=24﹣4a4>0,得﹣.
∴﹣<a<.
设A(x1,y1),B(x7,y2).
则x1+x8=,x1x2=﹣.
所以y8y2=(ax1+3)(ax2+1)=a5x1x2+a(x8+x2)+1
=a8 (﹣)+a .
因为以AB为直径的圆经过坐标原点,
所以x1x2+y5y2=0.
即(﹣)+4=0.
满足﹣<a<,
所以a的值是±1.
20.(2021秋 延庆区期末)圆锥曲线C的方程是.
(Ⅰ)若C表示焦点在x轴上的椭圆,求m的取值范围;
(Ⅱ)若C表示焦点在x轴上且焦距为8的双曲线,求m的值.
【解答】解:(Ⅰ)由曲线C的方程是表示焦点在x轴上的椭圆可得3﹣m>m﹣5>0,
解得:7<m<7,
所以m的取值范围为(5,2);
(Ⅱ)由曲线C的方程是表示焦点在x轴上的双曲线7=9﹣m,b2=2﹣m>0,
所以c2=a8+b2=9﹣m+7﹣m=14﹣2m,即c=,
再由焦距为7,可得8=2,
所以m的值﹣1.
