第4章幂指数、指数函数与对数函数 单元测试-数学沪教版(2020)必修第一册(含解析)
文档属性
| 名称 | 第4章幂指数、指数函数与对数函数 单元测试-数学沪教版(2020)必修第一册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 308.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 04:37:43 | ||
图片预览


文档简介
沪教版(2020)幂指数、指数函数与对数函数单元测试
(共21题,共150分)
一、选择题(共10题,共50分)
(5分)如果函数 的图象经过点 ,那么实数 的值为
A. B. C. D.
(5分)化简 的结果是
A. B. C. D.
(5分)下列各函数中,是指数函数的是
A. B. C. D.
(5分)函数 ( ,且 )的图象恒过某定点,则此定点为
A. B. C. D.
(5分)已知函数 (其中 ),若 的图象如下图所示,则函数 的图象是
A. B.
C. D.
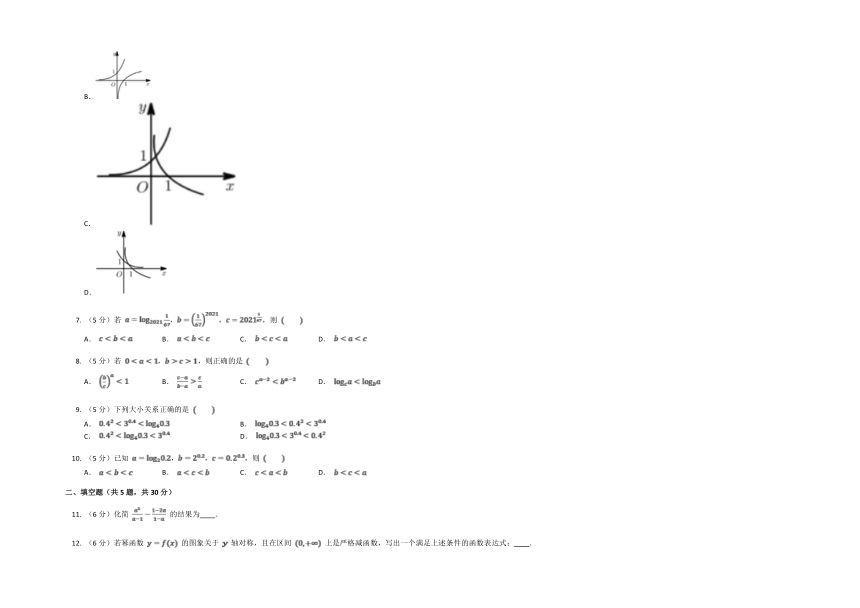
(5分)当 时,在同一坐标系中,函数 的图象是
A.
B.
C.
D.
(5分)若 ,,,则
A. B. C. D.
(5分)若 ,,则正确的是
A. B. C. D.
(5分)下列大小关系正确的是
A. B.
C. D.
(5分)已知 ,,,则
A. B. C. D.
二、填空题(共5题,共30分)
(6分)化简 的结果为 .
(6分)若幂函数 的图象关于 轴对称,且在区间 上是严格减函数,写出一个满足上述条件的函数表达式: .
(6分)函数 ( 且 )恒过定点 .
(6分)“当 时,能使不等式 ”成立的一组正数 , 的值依次 .
(6分)设 ,若 ,则实数 的取值范围是 .
三、解答题(共6题,共70分)
(10分)请回答:
(1) 求值:;
(2) 若 ,,用 , 表示 .
(12分)设函数 ,若 ,求实数 的取值范围.
(12分)已知函数 ,且 ,求实数 的值.
(12分)函数 (,且 )在 上的最大值比最小值大 ,求 的值.
(12分)设 ,且 ,若 ,,试比较 , 的大小.
(12分)已知全集 ,集合 ,,求 .
答案
一、选择题(共10题,共50分)
1. 【答案】A
【知识点】幂的概念与运算
2. 【答案】A
【知识点】幂的概念与运算
3. 【答案】D
【解析】根据指数函数的概念知,D正确.
【知识点】指数函数及其性质
4. 【答案】B
【解析】令 ,得 ,
所以函数 的图象恒过定点 .
【知识点】指数函数及其性质
5. 【答案】A
【解析】由题图得 ,.故答案为A.
【知识点】函数图象、指数函数及其性质
6. 【答案】C
【解析】 时,,,为 上的增函数, 上的减函数.
【知识点】指数函数及其性质、对数函数及其性质
7. 【答案】B
【知识点】对数函数及其性质、指数函数及其性质
8. 【答案】D
【知识点】指数函数及其性质、对数函数及其性质、不等式的性质
9. 【答案】B
【解析】 ,,,
故 .
【知识点】指数函数及其性质、对数函数及其性质
10. 【答案】B
【知识点】对数函数及其性质、指数函数及其性质
二、填空题(共5题,共30分)
11. 【答案】
【解析】
【知识点】幂的概念与运算
12. 【答案】 (答案不唯一)
【知识点】幂函数及其性质
13. 【答案】
【解析】当 ,即 时,,故函数恒过定点 .
【知识点】指数函数及其性质
14. 【答案】 ,
【知识点】对数函数及其性质
15. 【答案】
【知识点】对数函数及其性质
三、解答题(共6题,共70分)
16. 【答案】
(1)
(2) 因为 ,,
所以 ,,
所以
【知识点】对数的概念与运算、幂的概念与运算
17. 【答案】当 时,不等式 可化为 ,即 ,解得 ;
当 时,不等式 可化为 ,所以 .
综上, 的取值范围是 .
【知识点】指数函数及其性质、分段函数
18. 【答案】 或 .
【知识点】指数函数及其性质
19. 【答案】当 时,函数 在 上的最大值是 ,最小值是 ,依题意得 ,即 ,所以 ;
当 时,函数 在 上的最大值是 ,最小值是 ,依题意得 ,即 ,所以 .
综上可知, 或 .
【知识点】指数函数及其性质
20. 【答案】对底数 按照 和 分类讨论,应用了分类讨论思想.
当 时,有 ,即 .
又 在区间 上单调递减,
所以 ,即 .
当 时,有 ,即 .
又 在区间 上单调递增,
所以 ,即 .
综上,.
【知识点】对数函数及其性质
21. 【答案】由已知 ,
所以 ,,,
由 ,解得 ,
所以 .
于是 ,
所以 .
【知识点】对数函数及其性质、交、并、补集运算
(共21题,共150分)
一、选择题(共10题,共50分)
(5分)如果函数 的图象经过点 ,那么实数 的值为
A. B. C. D.
(5分)化简 的结果是
A. B. C. D.
(5分)下列各函数中,是指数函数的是
A. B. C. D.
(5分)函数 ( ,且 )的图象恒过某定点,则此定点为
A. B. C. D.
(5分)已知函数 (其中 ),若 的图象如下图所示,则函数 的图象是
A. B.
C. D.
(5分)当 时,在同一坐标系中,函数 的图象是
A.
B.
C.
D.
(5分)若 ,,,则
A. B. C. D.
(5分)若 ,,则正确的是
A. B. C. D.
(5分)下列大小关系正确的是
A. B.
C. D.
(5分)已知 ,,,则
A. B. C. D.
二、填空题(共5题,共30分)
(6分)化简 的结果为 .
(6分)若幂函数 的图象关于 轴对称,且在区间 上是严格减函数,写出一个满足上述条件的函数表达式: .
(6分)函数 ( 且 )恒过定点 .
(6分)“当 时,能使不等式 ”成立的一组正数 , 的值依次 .
(6分)设 ,若 ,则实数 的取值范围是 .
三、解答题(共6题,共70分)
(10分)请回答:
(1) 求值:;
(2) 若 ,,用 , 表示 .
(12分)设函数 ,若 ,求实数 的取值范围.
(12分)已知函数 ,且 ,求实数 的值.
(12分)函数 (,且 )在 上的最大值比最小值大 ,求 的值.
(12分)设 ,且 ,若 ,,试比较 , 的大小.
(12分)已知全集 ,集合 ,,求 .
答案
一、选择题(共10题,共50分)
1. 【答案】A
【知识点】幂的概念与运算
2. 【答案】A
【知识点】幂的概念与运算
3. 【答案】D
【解析】根据指数函数的概念知,D正确.
【知识点】指数函数及其性质
4. 【答案】B
【解析】令 ,得 ,
所以函数 的图象恒过定点 .
【知识点】指数函数及其性质
5. 【答案】A
【解析】由题图得 ,.故答案为A.
【知识点】函数图象、指数函数及其性质
6. 【答案】C
【解析】 时,,,为 上的增函数, 上的减函数.
【知识点】指数函数及其性质、对数函数及其性质
7. 【答案】B
【知识点】对数函数及其性质、指数函数及其性质
8. 【答案】D
【知识点】指数函数及其性质、对数函数及其性质、不等式的性质
9. 【答案】B
【解析】 ,,,
故 .
【知识点】指数函数及其性质、对数函数及其性质
10. 【答案】B
【知识点】对数函数及其性质、指数函数及其性质
二、填空题(共5题,共30分)
11. 【答案】
【解析】
【知识点】幂的概念与运算
12. 【答案】 (答案不唯一)
【知识点】幂函数及其性质
13. 【答案】
【解析】当 ,即 时,,故函数恒过定点 .
【知识点】指数函数及其性质
14. 【答案】 ,
【知识点】对数函数及其性质
15. 【答案】
【知识点】对数函数及其性质
三、解答题(共6题,共70分)
16. 【答案】
(1)
(2) 因为 ,,
所以 ,,
所以
【知识点】对数的概念与运算、幂的概念与运算
17. 【答案】当 时,不等式 可化为 ,即 ,解得 ;
当 时,不等式 可化为 ,所以 .
综上, 的取值范围是 .
【知识点】指数函数及其性质、分段函数
18. 【答案】 或 .
【知识点】指数函数及其性质
19. 【答案】当 时,函数 在 上的最大值是 ,最小值是 ,依题意得 ,即 ,所以 ;
当 时,函数 在 上的最大值是 ,最小值是 ,依题意得 ,即 ,所以 .
综上可知, 或 .
【知识点】指数函数及其性质
20. 【答案】对底数 按照 和 分类讨论,应用了分类讨论思想.
当 时,有 ,即 .
又 在区间 上单调递减,
所以 ,即 .
当 时,有 ,即 .
又 在区间 上单调递增,
所以 ,即 .
综上,.
【知识点】对数函数及其性质
21. 【答案】由已知 ,
所以 ,,,
由 ,解得 ,
所以 .
于是 ,
所以 .
【知识点】对数函数及其性质、交、并、补集运算
同课章节目录
