2022—2023学年鲁教版(五四制)数学九年级上册2.6利用三角函数测高 课件(共14张PPT)
文档属性
| 名称 | 2022—2023学年鲁教版(五四制)数学九年级上册2.6利用三角函数测高 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 820.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 18:12:35 | ||
图片预览



文档简介
(共14张PPT)
2.6 利用三角函数测高
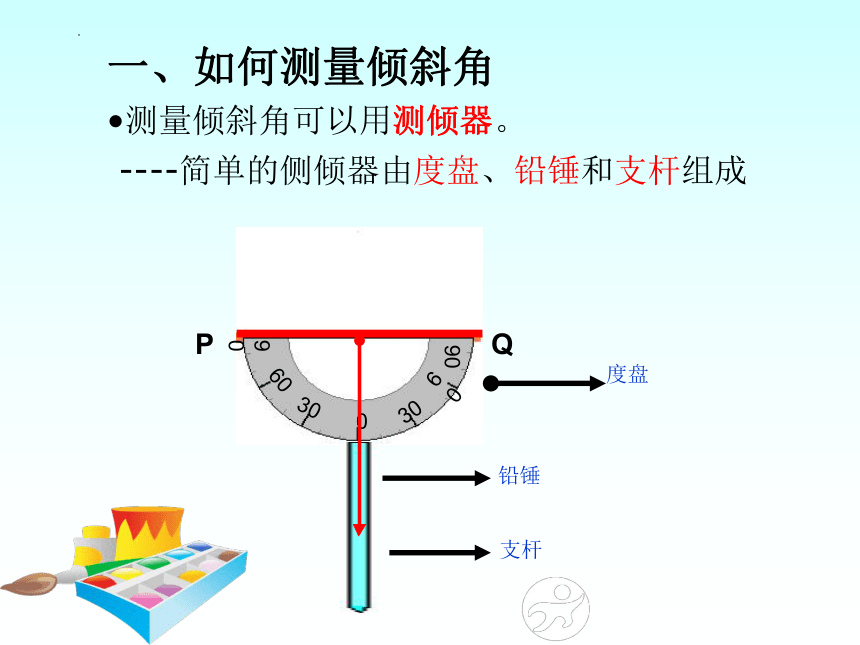
一、如何测量倾斜角
测量倾斜角可以用测倾器。
----简单的侧倾器由度盘、铅锤和支杆组成
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
0
30
30
60
60
90
90
使用测倾器测量倾斜角的步骤如下:
1、把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。
P
Q
0
30
30
60
60
90
90
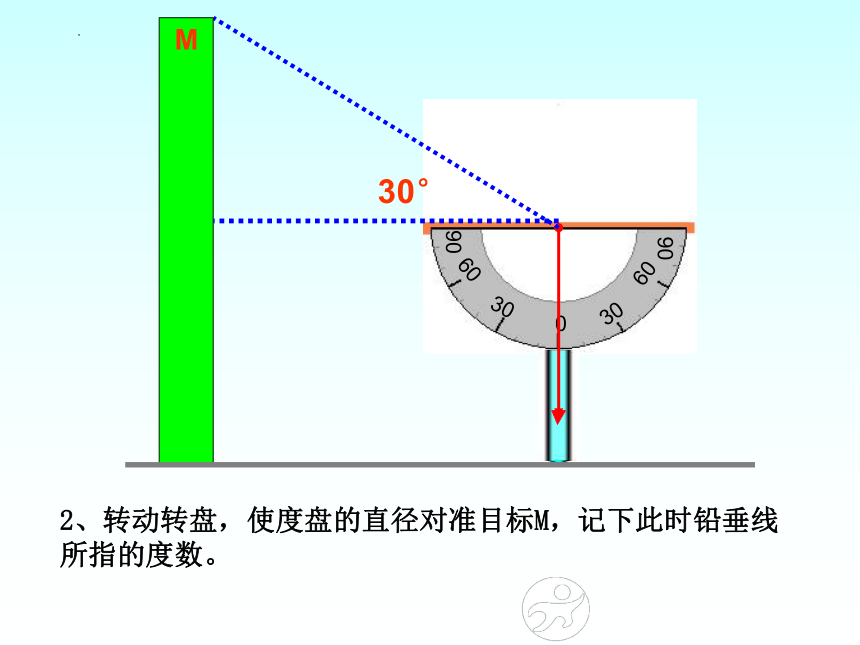
2、转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数。
M
30°
A
C
M
N
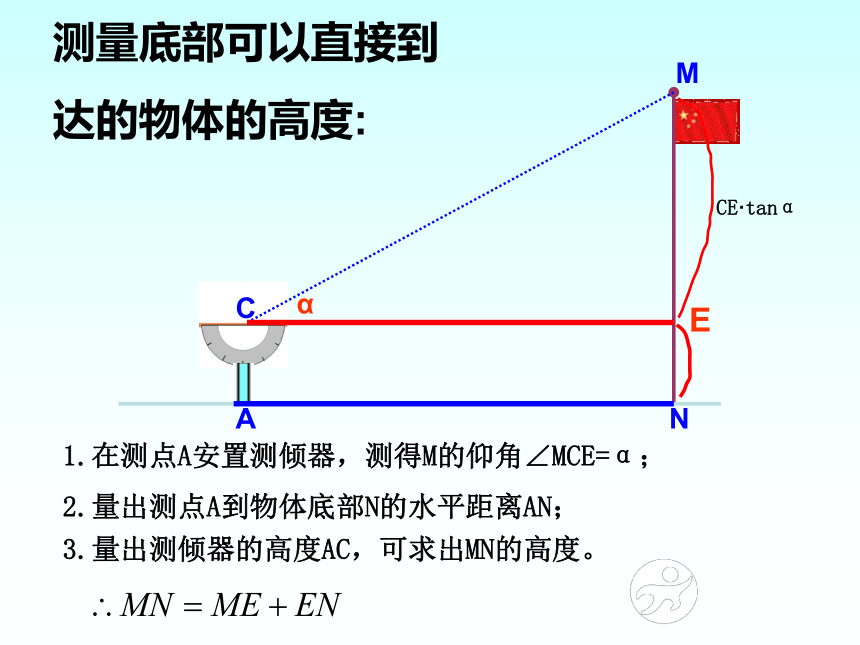
1.在测点A安置测倾器,测得M的仰角∠MCE=α;
E
2.量出测点A到物体底部N的水平距离AN;
3.量出测倾器的高度AC,可求出MN的高度。
测量底部可以直接到
达的物体的高度:
α
CE·tanα
例1 如图,小颖利用有一个锐角是30°的三角板测量一棵树
的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即
小颖的身高),那么这棵树高是 米。
解:∵BE=AD=5,∠CAD=30°
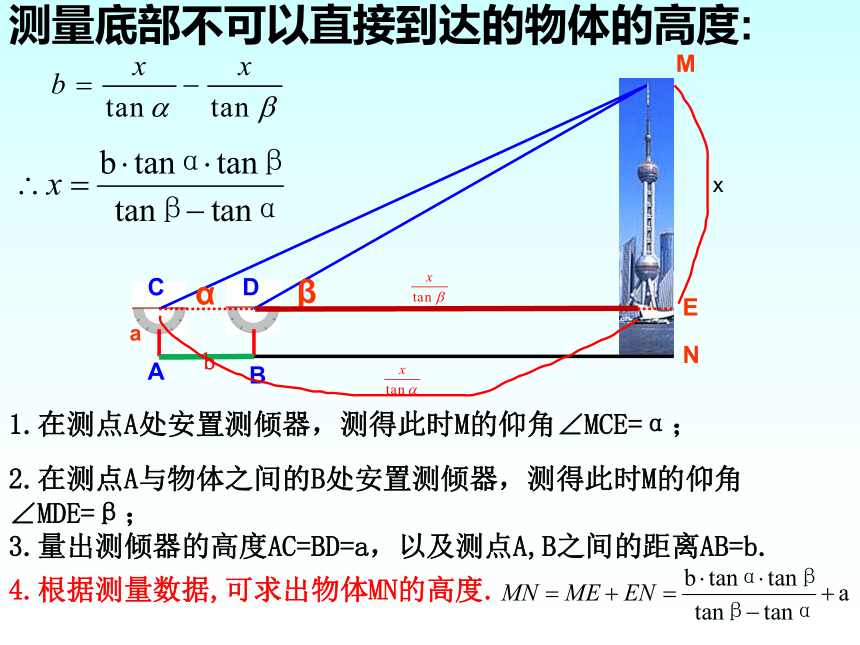
测量底部不可以直接到达的物体的高度:
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
A
C
B
D
M
N
E
α
2.在测点A与物体之间的B处安置测倾器,测得此时M的仰角 ∠MDE=β;
β
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
4.根据测量数据,可求出物体MN的高度.
x
b
a
例2 小亮想测得大厦的高度,用过学习,使用侧倾器测得∠α=30°,∠β=45°,AB=60米,若侧倾器高度忽略不计,请你帮忙计算大厦的高度是多少
45°
60
30°
解:设 ME = x 米
对应训练
1.如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:(即AB:BC=1: ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
2
4
x
M
1°在RT △ABC中,AB=2,
AB:BC=1:
2°在RT △ADM中, ∠ DAM=30°
设 DM=x
3°在RT △DCE中, ∠ DCE=60°,DE=(x+2), CE=
对应训练
1.如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:(即AB:BC=1: ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
2
4
x
M
解:在RT △ABC中,AB=2,
AB:BC=1:
在RT △ADM中, ∠ DAM=30°
设 DM=x,则
在RT △DCE中, ∠ DCE=60°,
DE=(x+2), CE=
DE = 4 + 2 = 6
答:树DE的高度为6米
1.测量底部可以到达的物体的高度.
b
课堂小结
α
b
a
MN = b·tanα + a
α
β
a
2.测量底部不可以到达的物体的高度.
x
b·tanα
六、当堂检测
C
A
3.如图,在一次数学课外实践活动中,要求测教学楼的高度AB.小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
七、拓展提升
1.如图,某军港有一雷达站 P,军舰 M 停泊在雷达站 P的南偏东60°方向36海里处,另一艘军舰 N 位于军舰 M 的正西方向,与雷达站 P 相距 海里.求:
(1)军舰N在雷达站P的什么方向?
(2)两军舰M、N 的距离.(结果保留根号)
60°
30°
D
36
18
18
45°
2.6 利用三角函数测高
一、如何测量倾斜角
测量倾斜角可以用测倾器。
----简单的侧倾器由度盘、铅锤和支杆组成
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
0
30
30
60
60
90
90
使用测倾器测量倾斜角的步骤如下:
1、把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。
P
Q
0
30
30
60
60
90
90
2、转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数。
M
30°
A
C
M
N
1.在测点A安置测倾器,测得M的仰角∠MCE=α;
E
2.量出测点A到物体底部N的水平距离AN;
3.量出测倾器的高度AC,可求出MN的高度。
测量底部可以直接到
达的物体的高度:
α
CE·tanα
例1 如图,小颖利用有一个锐角是30°的三角板测量一棵树
的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即
小颖的身高),那么这棵树高是 米。
解:∵BE=AD=5,∠CAD=30°
测量底部不可以直接到达的物体的高度:
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
A
C
B
D
M
N
E
α
2.在测点A与物体之间的B处安置测倾器,测得此时M的仰角 ∠MDE=β;
β
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
4.根据测量数据,可求出物体MN的高度.
x
b
a
例2 小亮想测得大厦的高度,用过学习,使用侧倾器测得∠α=30°,∠β=45°,AB=60米,若侧倾器高度忽略不计,请你帮忙计算大厦的高度是多少
45°
60
30°
解:设 ME = x 米
对应训练
1.如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:(即AB:BC=1: ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
2
4
x
M
1°在RT △ABC中,AB=2,
AB:BC=1:
2°在RT △ADM中, ∠ DAM=30°
设 DM=x
3°在RT △DCE中, ∠ DCE=60°,DE=(x+2), CE=
对应训练
1.如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:(即AB:BC=1: ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
2
4
x
M
解:在RT △ABC中,AB=2,
AB:BC=1:
在RT △ADM中, ∠ DAM=30°
设 DM=x,则
在RT △DCE中, ∠ DCE=60°,
DE=(x+2), CE=
DE = 4 + 2 = 6
答:树DE的高度为6米
1.测量底部可以到达的物体的高度.
b
课堂小结
α
b
a
MN = b·tanα + a
α
β
a
2.测量底部不可以到达的物体的高度.
x
b·tanα
六、当堂检测
C
A
3.如图,在一次数学课外实践活动中,要求测教学楼的高度AB.小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
七、拓展提升
1.如图,某军港有一雷达站 P,军舰 M 停泊在雷达站 P的南偏东60°方向36海里处,另一艘军舰 N 位于军舰 M 的正西方向,与雷达站 P 相距 海里.求:
(1)军舰N在雷达站P的什么方向?
(2)两军舰M、N 的距离.(结果保留根号)
60°
30°
D
36
18
18
45°
