2022—2023学年鲁教版(五四制)数学九年级上册2.5三角函数的应用(2)课件(共15张PPT)
文档属性
| 名称 | 2022—2023学年鲁教版(五四制)数学九年级上册2.5三角函数的应用(2)课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 18:13:49 | ||
图片预览




文档简介
(共15张PPT)
2.5 三角函数的应用(2)
学习目标
1.理解坡度,坡角的概念,能够把坡度问题转化成数学问题
2.进一步体会三角函数在解决实际问题中的作用
坡角
tanα
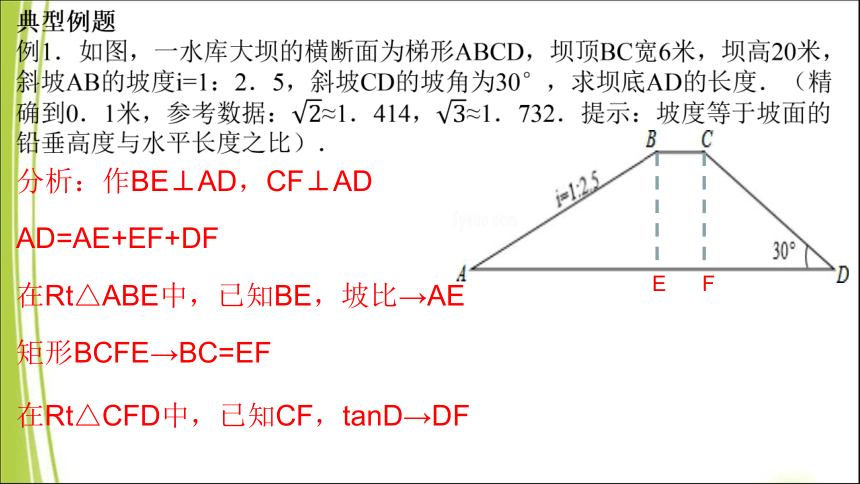
分析:作BE⊥AD,CF⊥AD
E F
AD=AE+EF+DF
在Rt△ABE中,已知BE,坡比→AE
矩形BCFE→BC=EF
在Rt△CFD中,已知CF,tanD→DF
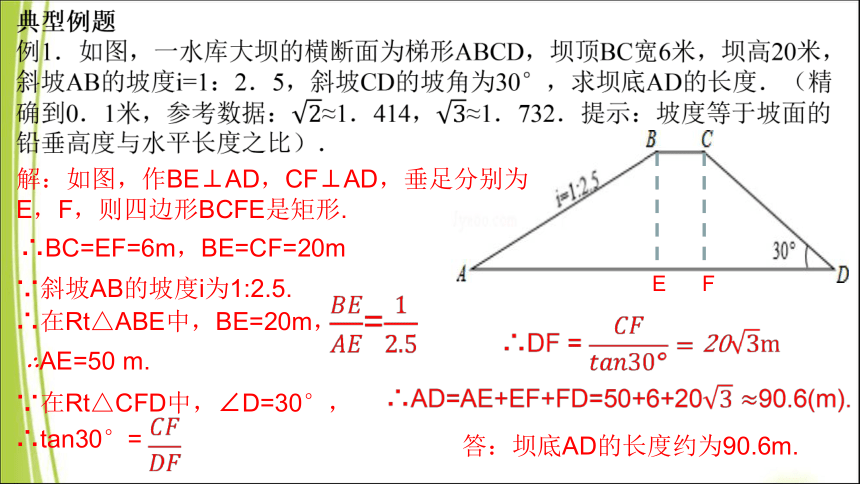
答:坝底AD的长度约为90.6m.
解:如图,作BE⊥AD,CF⊥AD,垂足分别为E,F,则四边形BCFE是矩形.
E F
∴BC=EF=6m,BE=CF=20m
∴AE=50 m.
∵斜坡AB的坡度i为1:2.5.
∴在Rt△ABE中,BE=20m,
∵在Rt△CFD中,∠D=30°,
∴tan30°=
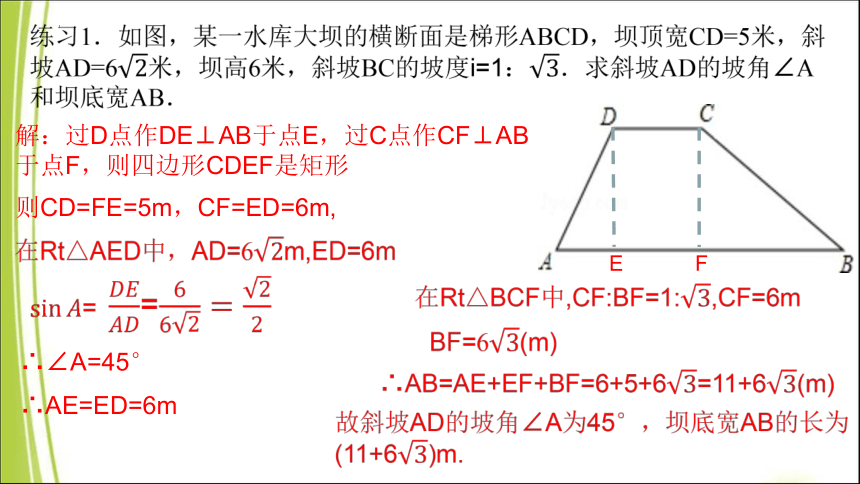
解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形
E F
则CD=FE=5m,CF=ED=6m,
∴∠A=45°
∴AE=ED=6m
例2.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长(精确到0.1米);
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,sin58°12′≈0.85,tan49°30′≈1.17)
例2.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长(精确到0.1米)(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48);
解:(1)在Rt△ABE中,AB=26,∠BAD=68°
∴sin∠BAD =
∴BE=AB·sin∠BAD=26×sin 68°=26×0.93≈24.2m
∴改造前坡顶到地面的距离BE的长为24.2m
例2.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?(参考数据:cos68°≈0.37,sin58°12′≈0.85,tan49°30′≈1.17)
M
(2)分析:过点F作FM⊥AD于点M,连接AF
可得FM,AM
在Rt△AFM中,可求tan∠ FAM→可求∠FAM
在Rt△ABE中,cos∠BAE→AE
比较∠FAM与50°大小关系
例2.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?(参考数据:cos68°≈0.37,sin58°12′≈0.85,tan49°30′≈1.17)
∴∠FAM≈49°30'<50°
M
(2)过点F作FM⊥AD于点M,连接AF
∵BE⊥AD,BCIlAD,BF =11,
∴FM=BE=24.2,EM=BF=11.
在Rt△ABE中,cos∠BAE=
∴AE=AB·cos∠BAE=26×cos68°=26×0.37≈9.62m.
AM=AE+EM=9.62+11=20.62m,
在Rt△AFM中,
tan∠ FAM= = ≈1.17
∴这样改造能确保安全.
2.如图,水库大坝的横断面为梯形,坝顶宽6m,坝高8m,
斜坡AB的坡角为45°,斜坡CD的坡度i=1:3,
则坝底宽BC为( )
A.36m B.72m C.78m D.38m
3.如图,某水库大坝的横断面是梯形ABCD,
坝顶宽AD=6米,坝高是20米,背水坡AB的
坡角为30°,迎水坡CD的坡度为1:2,那么
坝底BC的长度等于 米(结果保留根号)
当堂检测
1.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为α,
那么滑梯长l为( )
A. B. C. D.h sinα
A
D
30
解:
(1)
5.小丹要测量灯塔市葛西河生态公园里被湖水隔开的两个凉亭A和B之间的距离,她在A处测得凉亭B在A的南偏东75°方向,她从A处出发向南偏东30°方向走了300米到达C处,测得凉亭B在C的东北方向.
(2)求两个凉亭A和B之间的距离(结果保留根号).
D
45°
60°
拓展提升
1.如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台合风中心距离小岛200海里.
(1)过点B作BP⊥AC于点P,求∠PBC的度数;
解:
2.5 三角函数的应用(2)
学习目标
1.理解坡度,坡角的概念,能够把坡度问题转化成数学问题
2.进一步体会三角函数在解决实际问题中的作用
坡角
tanα
分析:作BE⊥AD,CF⊥AD
E F
AD=AE+EF+DF
在Rt△ABE中,已知BE,坡比→AE
矩形BCFE→BC=EF
在Rt△CFD中,已知CF,tanD→DF
答:坝底AD的长度约为90.6m.
解:如图,作BE⊥AD,CF⊥AD,垂足分别为E,F,则四边形BCFE是矩形.
E F
∴BC=EF=6m,BE=CF=20m
∴AE=50 m.
∵斜坡AB的坡度i为1:2.5.
∴在Rt△ABE中,BE=20m,
∵在Rt△CFD中,∠D=30°,
∴tan30°=
解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形
E F
则CD=FE=5m,CF=ED=6m,
∴∠A=45°
∴AE=ED=6m
例2.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长(精确到0.1米);
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,sin58°12′≈0.85,tan49°30′≈1.17)
例2.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长(精确到0.1米)(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48);
解:(1)在Rt△ABE中,AB=26,∠BAD=68°
∴sin∠BAD =
∴BE=AB·sin∠BAD=26×sin 68°=26×0.93≈24.2m
∴改造前坡顶到地面的距离BE的长为24.2m
例2.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?(参考数据:cos68°≈0.37,sin58°12′≈0.85,tan49°30′≈1.17)
M
(2)分析:过点F作FM⊥AD于点M,连接AF
可得FM,AM
在Rt△AFM中,可求tan∠ FAM→可求∠FAM
在Rt△ABE中,cos∠BAE→AE
比较∠FAM与50°大小关系
例2.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?(参考数据:cos68°≈0.37,sin58°12′≈0.85,tan49°30′≈1.17)
∴∠FAM≈49°30'<50°
M
(2)过点F作FM⊥AD于点M,连接AF
∵BE⊥AD,BCIlAD,BF =11,
∴FM=BE=24.2,EM=BF=11.
在Rt△ABE中,cos∠BAE=
∴AE=AB·cos∠BAE=26×cos68°=26×0.37≈9.62m.
AM=AE+EM=9.62+11=20.62m,
在Rt△AFM中,
tan∠ FAM= = ≈1.17
∴这样改造能确保安全.
2.如图,水库大坝的横断面为梯形,坝顶宽6m,坝高8m,
斜坡AB的坡角为45°,斜坡CD的坡度i=1:3,
则坝底宽BC为( )
A.36m B.72m C.78m D.38m
3.如图,某水库大坝的横断面是梯形ABCD,
坝顶宽AD=6米,坝高是20米,背水坡AB的
坡角为30°,迎水坡CD的坡度为1:2,那么
坝底BC的长度等于 米(结果保留根号)
当堂检测
1.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为α,
那么滑梯长l为( )
A. B. C. D.h sinα
A
D
30
解:
(1)
5.小丹要测量灯塔市葛西河生态公园里被湖水隔开的两个凉亭A和B之间的距离,她在A处测得凉亭B在A的南偏东75°方向,她从A处出发向南偏东30°方向走了300米到达C处,测得凉亭B在C的东北方向.
(2)求两个凉亭A和B之间的距离(结果保留根号).
D
45°
60°
拓展提升
1.如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台合风中心距离小岛200海里.
(1)过点B作BP⊥AC于点P,求∠PBC的度数;
解:
