2022—2023学年鲁教版(五四制)数学九年级上册2.5三角函数的应用(1)课件(共14张PPT)
文档属性
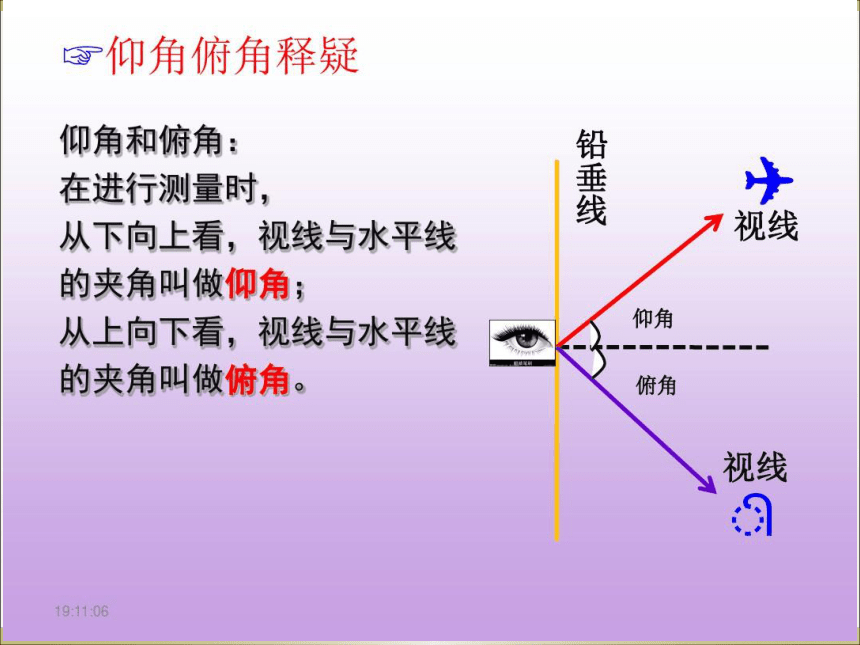
| 名称 | 2022—2023学年鲁教版(五四制)数学九年级上册2.5三角函数的应用(1)课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 798.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 00:00:00 | ||
图片预览

文档简介
(共14张PPT)
2.5 三角函数的应用(1)
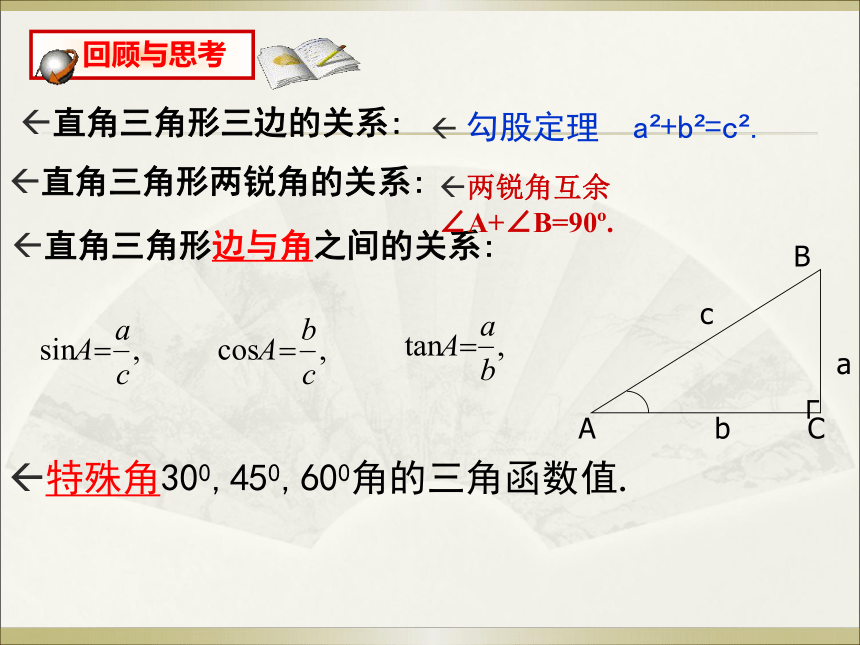
直角三角形两锐角的关系:
直角三角形三边的关系:
回顾与思考
b
A
B
C
a
┌
c
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:
勾股定理 a +b =c .
两锐角互余 ∠A+∠B=90 .
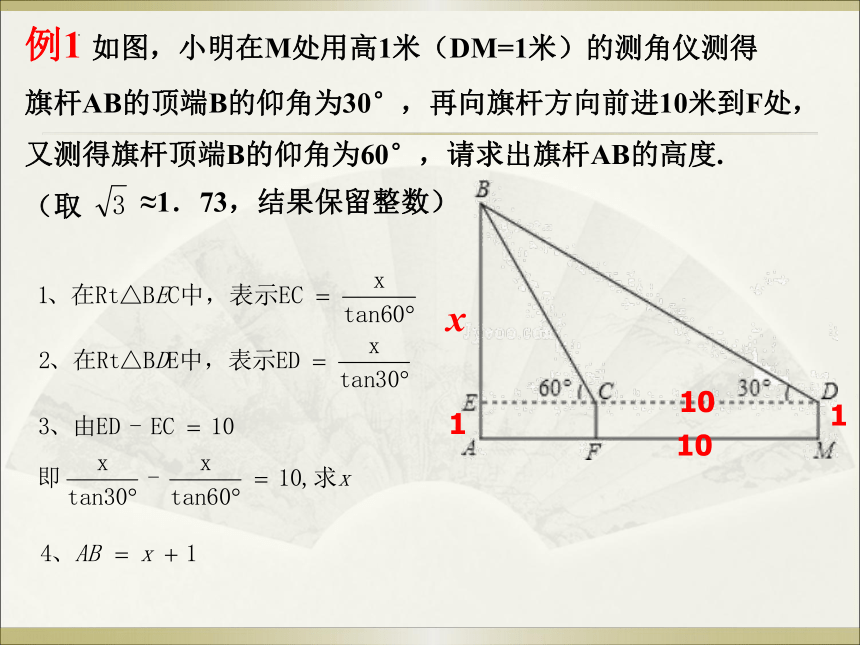
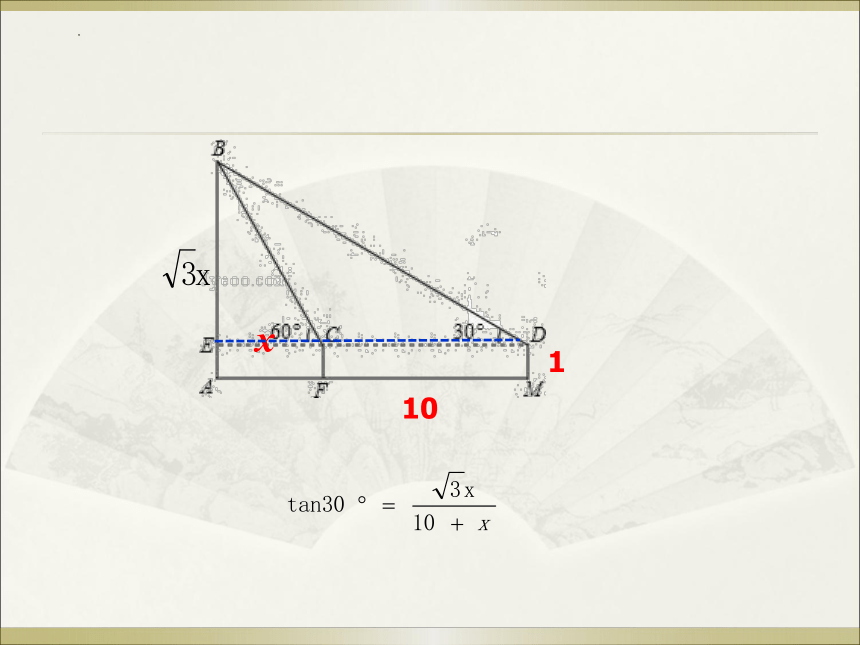
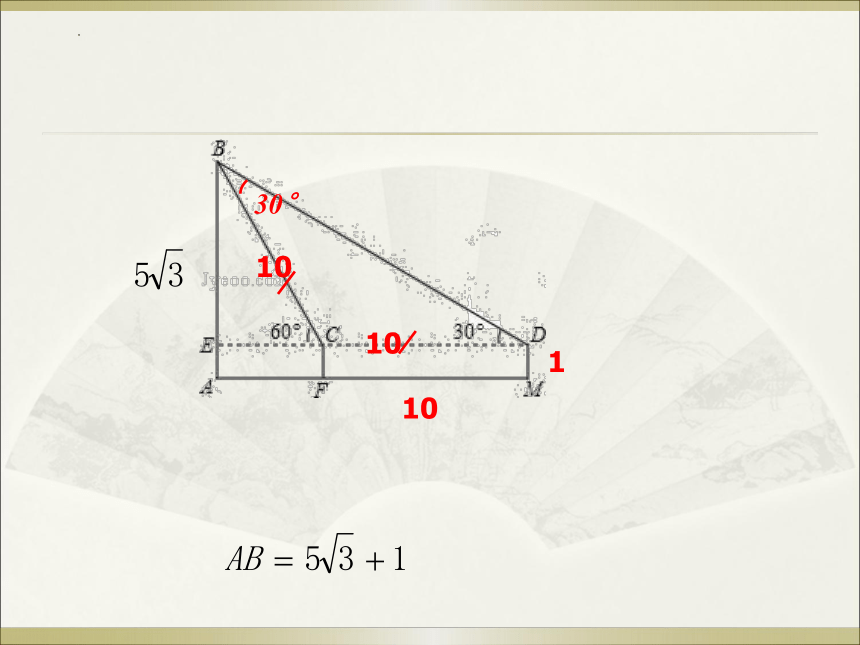
例1 如图,小明在M处用高1米(DM=1米)的测角仪测得
旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,
又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度.
(取
≈1.73,结果保留整数)
1
x
10
10
1
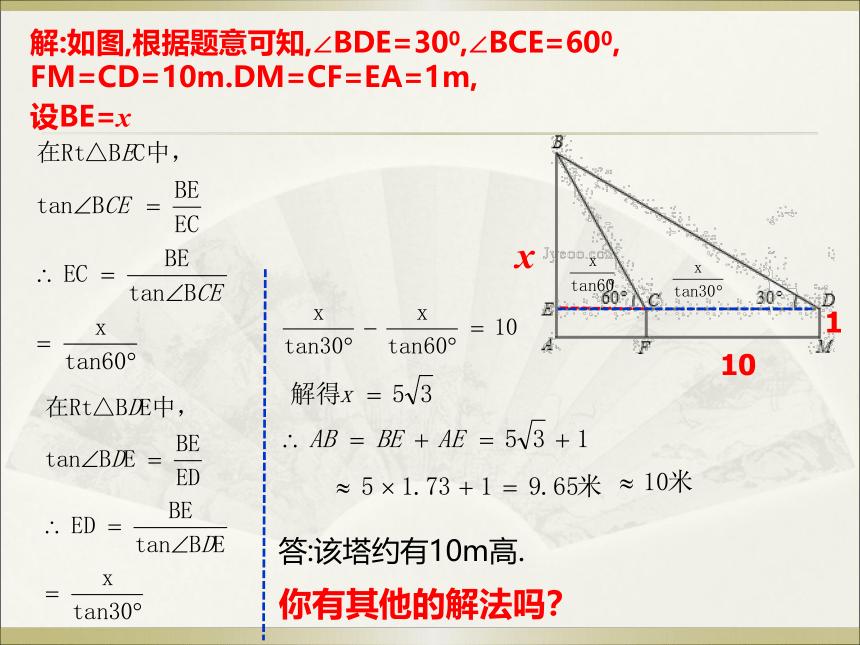
答:该塔约有10m高.
解:如图,根据题意可知,∠BDE=300,∠BCE=600,
FM=CD=10m.DM=CF=EA=1m,
你有其他的解法吗?
1
10
x
设BE=x
1
10
x
1
10
30°
10
10
例2.某公园中有条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨利用它们测量小河的宽度,于是,他去了河边,如图.他从河的南岸石墩A处测得大树P在其北偏东30°方向,然后他沿正东方向步行80米到达点B处,此时测得大树P在其北偏西60°方向.请根据以上所测得的数据,计算小河的宽度.(结果保留根号)
80
60°
30°
D
1、方位角转化为△PAB的内角
2、过P点做PD⊥AB于点D,构造Rt△PBD
3、在Rt△PAB中,求PB
在Rt△PBD中,求PD
例2.某公园中有条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨利用它们测量小河的宽度,于是,他去了河边,如图.他从河的南岸石墩A处测得大树P在其北偏东30°方向,然后他沿正东方向步行80米到达点B处,此时测得大树P在其北偏西60°方向.请根据以上所测得的数据,计算小河的宽度.(结果保留根号)
80
60°
30°
D
解:如图,根据题意可知,
在△PAB中,
∠PAB=600,∠PBA=300,
∴ ∠APB=900
过P点做PD⊥AB于点D
答:小河的宽度为
对应训练1 如图,小亮为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45° .已知测角仪的高度是1.5m,请你计算出该建筑物的高度.
1.5
x
x
船有无触礁的危险
海中有一个小岛A,该岛四周10海里内暗礁.今有货轮由西向东航行,开始在A岛南偏西600的B处,往东行驶20海里后到达该岛的南偏西300的C处.之后,货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗
请说明你的理由.
驶向胜利的彼岸
A
B
C
D
北
东
对应训练2
D
┌
>10
所以不可能触礁
10
五、当堂检测
1.如图,已知△ABC是直角三角形,∠DAC=45°,∠BAC=60°,AC=20m,则BD的长度是 .
2.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
20
5
5
30°
3.数学兴趣小组活动课上测量电线杆的高度.在位于电线杆同侧的A、B处(点A、B及电线杆底部F在同一条直线上),测得电线杆顶部E的仰角分别为36°和45°(如图所示).已知测量仪器距离地面都是1.5m,两测点A、B的距离是12m,求电线杆EF的高度.
(tan54°≈1.38,结果精确到0.1m)
H
x
x
12
六、拓展提升
2.5 三角函数的应用(1)
直角三角形两锐角的关系:
直角三角形三边的关系:
回顾与思考
b
A
B
C
a
┌
c
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:
勾股定理 a +b =c .
两锐角互余 ∠A+∠B=90 .
例1 如图,小明在M处用高1米(DM=1米)的测角仪测得
旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,
又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度.
(取
≈1.73,结果保留整数)
1
x
10
10
1
答:该塔约有10m高.
解:如图,根据题意可知,∠BDE=300,∠BCE=600,
FM=CD=10m.DM=CF=EA=1m,
你有其他的解法吗?
1
10
x
设BE=x
1
10
x
1
10
30°
10
10
例2.某公园中有条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨利用它们测量小河的宽度,于是,他去了河边,如图.他从河的南岸石墩A处测得大树P在其北偏东30°方向,然后他沿正东方向步行80米到达点B处,此时测得大树P在其北偏西60°方向.请根据以上所测得的数据,计算小河的宽度.(结果保留根号)
80
60°
30°
D
1、方位角转化为△PAB的内角
2、过P点做PD⊥AB于点D,构造Rt△PBD
3、在Rt△PAB中,求PB
在Rt△PBD中,求PD
例2.某公园中有条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨利用它们测量小河的宽度,于是,他去了河边,如图.他从河的南岸石墩A处测得大树P在其北偏东30°方向,然后他沿正东方向步行80米到达点B处,此时测得大树P在其北偏西60°方向.请根据以上所测得的数据,计算小河的宽度.(结果保留根号)
80
60°
30°
D
解:如图,根据题意可知,
在△PAB中,
∠PAB=600,∠PBA=300,
∴ ∠APB=900
过P点做PD⊥AB于点D
答:小河的宽度为
对应训练1 如图,小亮为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45° .已知测角仪的高度是1.5m,请你计算出该建筑物的高度.
1.5
x
x
船有无触礁的危险
海中有一个小岛A,该岛四周10海里内暗礁.今有货轮由西向东航行,开始在A岛南偏西600的B处,往东行驶20海里后到达该岛的南偏西300的C处.之后,货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗
请说明你的理由.
驶向胜利的彼岸
A
B
C
D
北
东
对应训练2
D
┌
>10
所以不可能触礁
10
五、当堂检测
1.如图,已知△ABC是直角三角形,∠DAC=45°,∠BAC=60°,AC=20m,则BD的长度是 .
2.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
20
5
5
30°
3.数学兴趣小组活动课上测量电线杆的高度.在位于电线杆同侧的A、B处(点A、B及电线杆底部F在同一条直线上),测得电线杆顶部E的仰角分别为36°和45°(如图所示).已知测量仪器距离地面都是1.5m,两测点A、B的距离是12m,求电线杆EF的高度.
(tan54°≈1.38,结果精确到0.1m)
H
x
x
12
六、拓展提升
