13.1.2线段的垂直平分线的性质(1)课件(共31张PPT)
文档属性
| 名称 | 13.1.2线段的垂直平分线的性质(1)课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 22:09:16 | ||
图片预览









文档简介
(共31张PPT)
人教版 八年级上册
13.1.2 线段的垂直平分线的性质 (1)
教学目标
1.经历探索、证明线段垂直平分线的性质定理和判定定理的过程,进一步发展学生的推理意识和能力.
2.能够在理解定理的基础上进行应用,建立数学来源于生活并服务于生活的思想.
教学重点:线段垂直平分线的性质定理
教学难点:线段垂直平分线性质定理的运用及综合运用
(1)定义:如果两个图形关于一条 对称,那么这两个图形关于这条直线成轴对称,这条直线叫做 .
1.轴对称
(2)性质
①关于某条直线成对称的两个图形是 形;
②如果两个图形关于某条直线对称,那么对称轴是对称点连线的 ;
③当两个图形关于某条直线对称时,如果它们的对应线段或延长线相交,那么交点一在 上.
对称轴
对称轴
直线
全等
垂直平分线
复习旧知
(1)定义:如果一个图形沿着一条直线折叠后,直线两旁的部分能够互相 ,那么这个图形叫做轴对称图形.这条直线叫做对称轴.
2.轴对称图形
重合
(3)轴对称和轴对称图形的区别
轴对称涉及两个图形,是两个图形的位置关系;
轴对称图形是对一个图形本身而言的.
(2)性质
①轴对称图形对应点所连的线段被对称轴 ;
②轴对称图形的对应线段 ,对应角 ;
垂直平分
相等
相等
1.下列图形中,不是轴对称图形的是 ( ) .
D
A B C D
2.在下列对称图形中,对称轴的条数最少的图形是( ).
A.圆 B.等边三角形 C.正方形 D.正六边形
B
3. 下列图形中是轴对称图形的是( ).
A.①② B.③④ C.②③ D.①④
①
②
③
④
D
4.下列“禁止行人通行,注意危险,禁止非机动车通行,限速60”四个交通标志图中,为轴对称图形的是( ).
A B C D
B
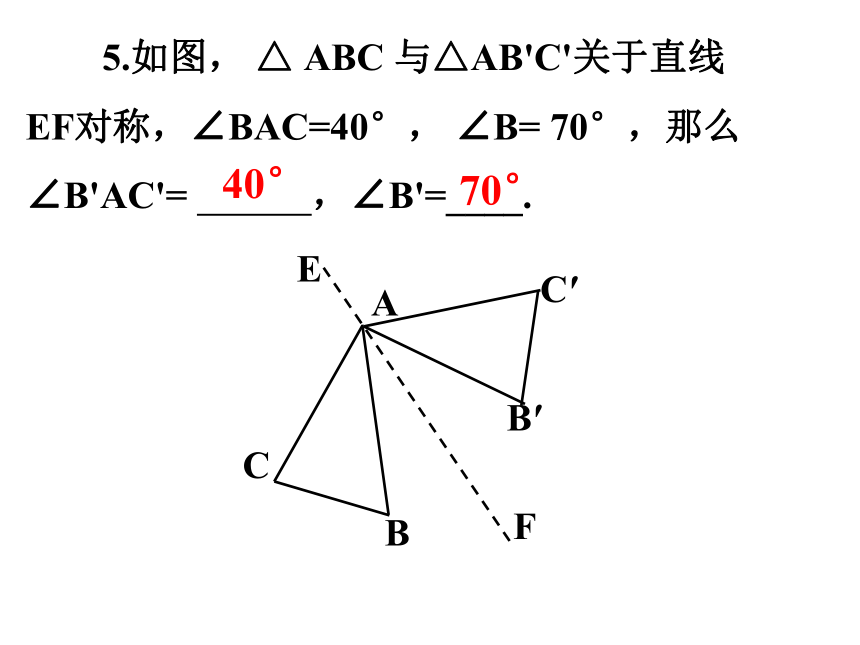
5.如图, △ ABC 与△AB'C'关于直线
EF对称,∠BAC=40°, ∠B= 70°,那么∠B'AC'= ,∠B'=____.
40°
70°
A
B
C
C′
B′
E
F
1.前面我们学习了轴对称图形,线段是轴对称图形吗?
2.你能找出线段的对称轴吗?
3. 线段的对称轴与这条线段有什么关系?说明理由.
线段的对称轴垂直平分这条线段.
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
设问导入
动手操作,归纳发现
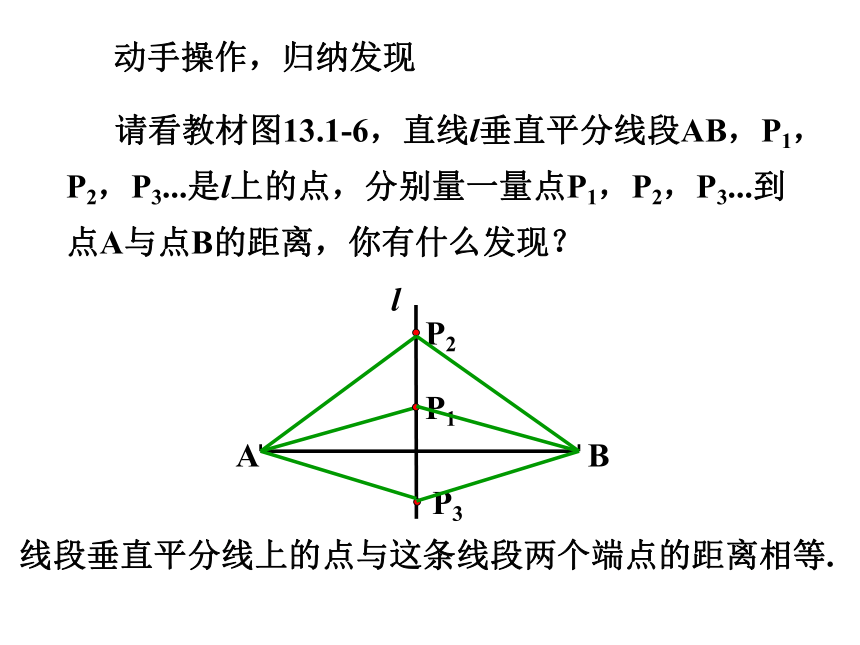
请看教材图13.1-6,直线l垂直平分线段AB,P1,P2,P3...是l上的点,分别量一量点P1,P2,P3...到点A与点B的距离,你有什么发现?
线段垂直平分线上的点与这条线段两个端点的距离相等.
A
P3
P2
P1
B
l
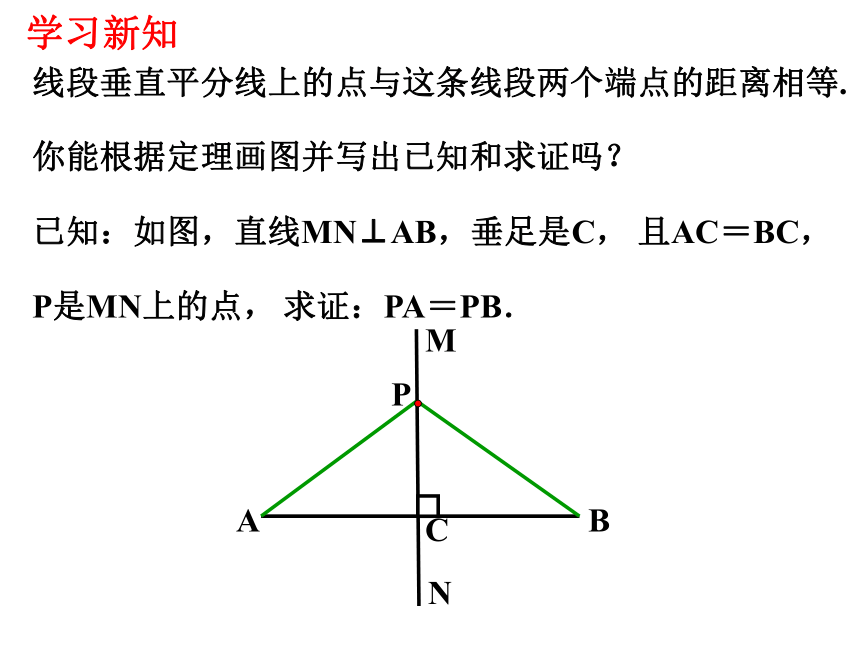
你能根据定理画图并写出已知和求证吗?
线段垂直平分线上的点与这条线段两个端点的距离相等.
已知:如图,直线MN⊥AB,垂足是C, 且AC=BC,
求证:PA=PB.
P是MN上的点,
A
N
M
B
P
C
学习新知
已知:如图,直线MN⊥AB,垂足是C, 且AC=BC,
求证:PA=PB.
P是MN上的点,
A
N
M
B
P
证明:
∵MN⊥AB,
∴∠PCA=∠PCB=90°.
∴PA=PB
∴△PCA≌△PCB
(全等三角形的对应边相等).
(SAS).
PC=PC,
AC=BC,
∠PCA=∠PCB.
在△PCA和△PCB中,
C
符号语言:
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵ MN⊥AB, AC=BC,
A
N
M
B
P
∴ PA=PB.
它是证明两条线段
相等的重要方法.
C
你能写出线段垂直平分线性质定理的逆命题吗?
它是真命题吗?
逆命题:
与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上.
线段垂直平分线上的点,
点与这条线段两个端点的距离相等.
线段垂直平分线上的点与这条线段两个端点的距离相等.
(已知).
(结论).
(已知).
(结论).
已知:如图,PA=PB,
求证:点P在AB的垂直平分线上。
C
M
A
B
P
证明:
过点P作PM⊥AB,垂足为C,
∴∠PCA=∠PCB=90°.
∴AC=BC
∴Rt△PAC≌Rt△PBC
(全等三角形的对应边相等).
(HL).
PC=PC,
PA=PB,
在Rt△PAC和R t△PBC中,
∴PM是AB的垂直平分线,
∴点P在AB的垂直平分线上.
符号语言:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵ PA=PB,
A
N
M
B
P
∴ 点P在AB的垂直平分线上.
它是证明两线的垂直关系的重要方法.
C
1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上。
AB、AC、CE的长度有什么关系?
AB+BD与DE有什么关系?
A
D
C
B
E
学以致用
1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上。
AB、AC、CE的长度有什么关系?
A
D
C
B
E
答:AB=AC=CE。
理由如下:
∵ AD⊥BC, BD=DC,
∴AD是BC的垂直平分线,
∴AB=AC.
∵点C在AE的垂直平分线上,
∴CE=CA,
∴AB=AC=CE.
1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上。
AB、AC、CE的长度有什么关系?
AB+BD与DE有什么关系?
A
D
C
B
E
答:AB+BD=DE.
理由如下:
∵ AB=CE, BD=DC,
∴AB+BD=CE+DC,
∴AB+BD=DE.
2.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
答:直线AM是BC的垂直平分线.
A
M
C
B
理由如下:
∵ AB=AC,
∴点A在BC的垂直平分线上.
∵ MB=MC,
∴点M在BC的垂直平分线上.
∴AM是BC的垂直平分线.
(两点确定一直线线)
3. 如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7 cm,那么ED=_____cm.
∵AB是线段CD的垂直平分线,
∴EC=ED
又∵EC=7 cm,
∴ED=7 cm.
A
D
E
B
C
7
码头应建在线段的垂直平分线与A,B一侧的河岸边的交点上.
4. 如图,A、B表示两个仓库,要在A、B一侧的
河岸边建造一个码头,使它到两个仓库的距离相等,
码头应建在什么位置?说说理由.
理由是线段垂直平分线上的点与这条线段两个端点的距离相等.
课堂小结
通过本节课的学习,你有哪些收获?
线段垂直平分线的性质定理和判定定理。
线段垂直平分线的性质是解决线段相等问题的重要方法.
应用:
知识:
线段垂直平分线的判定可用来证明两线的垂直关系.
1.如图,直线CD是线段AB的垂直平分线, P为直线CD上的一点.已知线段PA=5,则线段 PB的长度为( ).
A.6 B.5 C.4 D.3
A
D
P
B
C
巩固提高
B
2.如图.在△ABC中,DE是AC的垂直平分线,AE=8,△ABD的周长是30,则△ABC的周长
是( ).
A.30 B.38 C.40 D.46
A
D
E
B
C
D
3.已知MN是线段AB的垂直平分线.当点P在MN 上运动时,PA,PB的长度都随之变化但总保持 .
4.如图 ,在四边形ABCD 中,AC⊥BD,垂足为点E. 且BE=DE,则BC DC(填“>” ,<"或“=”)
A
D
E
B
C
相等
=
5.如图,D为BC边上一点,且BC=BD+AD,则
AD= ,点D在 的垂直平分线上.
A
D
B
C
CD
AC
今天作业
课本P66页第9题
课本P65页第6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
13.1.2 线段的垂直平分线的性质 (1)
教学目标
1.经历探索、证明线段垂直平分线的性质定理和判定定理的过程,进一步发展学生的推理意识和能力.
2.能够在理解定理的基础上进行应用,建立数学来源于生活并服务于生活的思想.
教学重点:线段垂直平分线的性质定理
教学难点:线段垂直平分线性质定理的运用及综合运用
(1)定义:如果两个图形关于一条 对称,那么这两个图形关于这条直线成轴对称,这条直线叫做 .
1.轴对称
(2)性质
①关于某条直线成对称的两个图形是 形;
②如果两个图形关于某条直线对称,那么对称轴是对称点连线的 ;
③当两个图形关于某条直线对称时,如果它们的对应线段或延长线相交,那么交点一在 上.
对称轴
对称轴
直线
全等
垂直平分线
复习旧知
(1)定义:如果一个图形沿着一条直线折叠后,直线两旁的部分能够互相 ,那么这个图形叫做轴对称图形.这条直线叫做对称轴.
2.轴对称图形
重合
(3)轴对称和轴对称图形的区别
轴对称涉及两个图形,是两个图形的位置关系;
轴对称图形是对一个图形本身而言的.
(2)性质
①轴对称图形对应点所连的线段被对称轴 ;
②轴对称图形的对应线段 ,对应角 ;
垂直平分
相等
相等
1.下列图形中,不是轴对称图形的是 ( ) .
D
A B C D
2.在下列对称图形中,对称轴的条数最少的图形是( ).
A.圆 B.等边三角形 C.正方形 D.正六边形
B
3. 下列图形中是轴对称图形的是( ).
A.①② B.③④ C.②③ D.①④
①
②
③
④
D
4.下列“禁止行人通行,注意危险,禁止非机动车通行,限速60”四个交通标志图中,为轴对称图形的是( ).
A B C D
B
5.如图, △ ABC 与△AB'C'关于直线
EF对称,∠BAC=40°, ∠B= 70°,那么∠B'AC'= ,∠B'=____.
40°
70°
A
B
C
C′
B′
E
F
1.前面我们学习了轴对称图形,线段是轴对称图形吗?
2.你能找出线段的对称轴吗?
3. 线段的对称轴与这条线段有什么关系?说明理由.
线段的对称轴垂直平分这条线段.
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
设问导入
动手操作,归纳发现
请看教材图13.1-6,直线l垂直平分线段AB,P1,P2,P3...是l上的点,分别量一量点P1,P2,P3...到点A与点B的距离,你有什么发现?
线段垂直平分线上的点与这条线段两个端点的距离相等.
A
P3
P2
P1
B
l
你能根据定理画图并写出已知和求证吗?
线段垂直平分线上的点与这条线段两个端点的距离相等.
已知:如图,直线MN⊥AB,垂足是C, 且AC=BC,
求证:PA=PB.
P是MN上的点,
A
N
M
B
P
C
学习新知
已知:如图,直线MN⊥AB,垂足是C, 且AC=BC,
求证:PA=PB.
P是MN上的点,
A
N
M
B
P
证明:
∵MN⊥AB,
∴∠PCA=∠PCB=90°.
∴PA=PB
∴△PCA≌△PCB
(全等三角形的对应边相等).
(SAS).
PC=PC,
AC=BC,
∠PCA=∠PCB.
在△PCA和△PCB中,
C
符号语言:
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵ MN⊥AB, AC=BC,
A
N
M
B
P
∴ PA=PB.
它是证明两条线段
相等的重要方法.
C
你能写出线段垂直平分线性质定理的逆命题吗?
它是真命题吗?
逆命题:
与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上.
线段垂直平分线上的点,
点与这条线段两个端点的距离相等.
线段垂直平分线上的点与这条线段两个端点的距离相等.
(已知).
(结论).
(已知).
(结论).
已知:如图,PA=PB,
求证:点P在AB的垂直平分线上。
C
M
A
B
P
证明:
过点P作PM⊥AB,垂足为C,
∴∠PCA=∠PCB=90°.
∴AC=BC
∴Rt△PAC≌Rt△PBC
(全等三角形的对应边相等).
(HL).
PC=PC,
PA=PB,
在Rt△PAC和R t△PBC中,
∴PM是AB的垂直平分线,
∴点P在AB的垂直平分线上.
符号语言:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵ PA=PB,
A
N
M
B
P
∴ 点P在AB的垂直平分线上.
它是证明两线的垂直关系的重要方法.
C
1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上。
AB、AC、CE的长度有什么关系?
AB+BD与DE有什么关系?
A
D
C
B
E
学以致用
1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上。
AB、AC、CE的长度有什么关系?
A
D
C
B
E
答:AB=AC=CE。
理由如下:
∵ AD⊥BC, BD=DC,
∴AD是BC的垂直平分线,
∴AB=AC.
∵点C在AE的垂直平分线上,
∴CE=CA,
∴AB=AC=CE.
1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上。
AB、AC、CE的长度有什么关系?
AB+BD与DE有什么关系?
A
D
C
B
E
答:AB+BD=DE.
理由如下:
∵ AB=CE, BD=DC,
∴AB+BD=CE+DC,
∴AB+BD=DE.
2.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
答:直线AM是BC的垂直平分线.
A
M
C
B
理由如下:
∵ AB=AC,
∴点A在BC的垂直平分线上.
∵ MB=MC,
∴点M在BC的垂直平分线上.
∴AM是BC的垂直平分线.
(两点确定一直线线)
3. 如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7 cm,那么ED=_____cm.
∵AB是线段CD的垂直平分线,
∴EC=ED
又∵EC=7 cm,
∴ED=7 cm.
A
D
E
B
C
7
码头应建在线段的垂直平分线与A,B一侧的河岸边的交点上.
4. 如图,A、B表示两个仓库,要在A、B一侧的
河岸边建造一个码头,使它到两个仓库的距离相等,
码头应建在什么位置?说说理由.
理由是线段垂直平分线上的点与这条线段两个端点的距离相等.
课堂小结
通过本节课的学习,你有哪些收获?
线段垂直平分线的性质定理和判定定理。
线段垂直平分线的性质是解决线段相等问题的重要方法.
应用:
知识:
线段垂直平分线的判定可用来证明两线的垂直关系.
1.如图,直线CD是线段AB的垂直平分线, P为直线CD上的一点.已知线段PA=5,则线段 PB的长度为( ).
A.6 B.5 C.4 D.3
A
D
P
B
C
巩固提高
B
2.如图.在△ABC中,DE是AC的垂直平分线,AE=8,△ABD的周长是30,则△ABC的周长
是( ).
A.30 B.38 C.40 D.46
A
D
E
B
C
D
3.已知MN是线段AB的垂直平分线.当点P在MN 上运动时,PA,PB的长度都随之变化但总保持 .
4.如图 ,在四边形ABCD 中,AC⊥BD,垂足为点E. 且BE=DE,则BC DC(填“>” ,<"或“=”)
A
D
E
B
C
相等
=
5.如图,D为BC边上一点,且BC=BD+AD,则
AD= ,点D在 的垂直平分线上.
A
D
B
C
CD
AC
今天作业
课本P66页第9题
课本P65页第6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
