青岛版2013-2014上学期九年级数学月考试题(无答案)
文档属性
| 名称 | 青岛版2013-2014上学期九年级数学月考试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-28 15:21:37 | ||
图片预览


文档简介
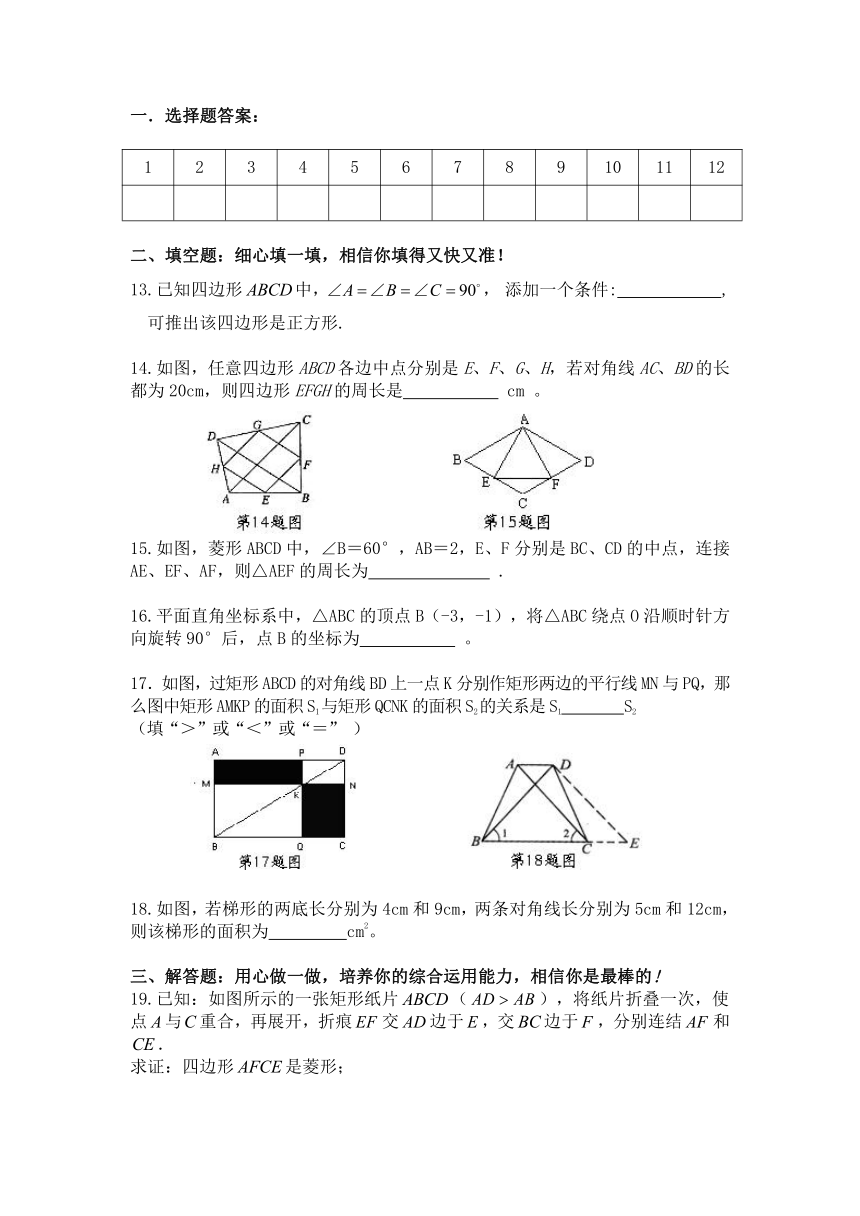
九年级数学第一次月考试题(青岛版)2013.10
一、选择题:精心选一选,想信你一定能选对!
1.下列图形中既是轴对称图形又是中心对称图形的是( )
2.不能判断四边形ABCD是平行四边形的条件是( )
A.AB∥CD,AD∥BC; B.AB = CD,AD = BC;
C.AB∥CD,AB = CD; D.AB = CD,AD∥BC
3.矩形、菱形、正方形都具有的性质是( )
A、对角线相等 B、对角线互相平分
C、对角线互相垂直 D、对角线平分对角
4. 如图,将ΔPQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A. (-2,-4) B. (-2,4) C.(2,-3) D.(-1,-3)
5.如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )
A. 4 B. 3 C. 2 D. 1
6.如图,在菱形ABCD中,,则菱形AB边上的高CE的长
是( )。
A. B. C. 5 D.10
7.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )
A.1 B.2 C. D.
8.如图,在口ABCD中,E是AD的中点,若S□ A B CD =1,则图中阴影部分的面积
为( )
A. B. C. D.
9. 如图:下列条件之一能使口ABCD成为菱形的 ( )
①AC⊥BD ② ∠BAD=900 ③ AB=AD ④ AC=BD
A. ①③ B. ②③ C. ③④ D. ①②③
10. 如图,把△ABC绕点C顺时针旋转某个角度后得到△,若∠A=40°,
∠1=70°,则旋转角等于( )
A.30° B.50° C.70° D.100°
11. 如图,在边长为2的正方形ABCD中,M为AD边的中点,延长MD至点E,使ME=MC,以DE为边做正方形DEFG,点D在边CD上,则DG的长是( )
A. B. C . D.
12. 如图1-6,在ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的
是( )
A. B.
C.四边形AECD是等腰梯形 D.
1
2
3
4
5
6
7
8
9
10
11
12
一.选择题答案:
二、填空题:细心填一填,相信你填得又快又准!
13.已知四边形中,, 添加一个条件: ,可推出该四边形是正方形.
14.如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为20cm,则四边形EFGH的周长是 cm 。
15.如图,菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为 .
16.平面直角坐标系中,△ABC的顶点B(-3,-1),将△ABC绕点O沿顺时针方向旋转90°后,点B的坐标为 。
17.如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的关系是S1 S2
(填“>”或“<”或“=” )
18.如图,若梯形的两底长分别为4cm和9cm,两条对角线长分别为5cm和12cm,则该梯形的面积为 cm2。
三、解答题:用心做一做,培养你的综合运用能力,相信你是最棒的!
19.已知:如图所示的一张矩形纸片(),将纸片折叠一次,使点与重合,再展开,折痕交边于,交边于,分别连结和.
求证:四边形是菱形;
20. 如图,方格纸中的每个小方格都是边长为1个单位的小正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
(1)画出△ABC关于坐标原点成中心对称的△A1B1C1;
(2)将Rt△ABC平移后得到点A2(-3,-4),写出点B2和,C2的坐标;
(3)将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A,B,C,,,试在图上画出Rt△A,B,C,,的图形,并写出各个顶点的坐标。
21.如图,在梯形中,,BD=CD, ∠BDC=900 ,AD=3,BC=8,求的长.
22.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
23.已知:如图,Rt△ABC中,AB=8,BC=10,将△ABC沿着BC方向平移,
(1)若平移的距离为4, 求出四边形ABB/D的面积
(2)若平移的距离为x, 四边形ABB/D的面积为y,列出y与x的函数关系式。
24.在中,,∠ABC=1200,将绕点顺时针旋转角得交于点,分别交于两点.(1)如图1,观察并猜想,在旋转过程中,线段与有怎样的数量关系?并证明你的结论;
(2)如图2,当时,试判断四边形的形状,并说明理由;
一、选择题:精心选一选,想信你一定能选对!
1.下列图形中既是轴对称图形又是中心对称图形的是( )
2.不能判断四边形ABCD是平行四边形的条件是( )
A.AB∥CD,AD∥BC; B.AB = CD,AD = BC;
C.AB∥CD,AB = CD; D.AB = CD,AD∥BC
3.矩形、菱形、正方形都具有的性质是( )
A、对角线相等 B、对角线互相平分
C、对角线互相垂直 D、对角线平分对角
4. 如图,将ΔPQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A. (-2,-4) B. (-2,4) C.(2,-3) D.(-1,-3)
5.如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )
A. 4 B. 3 C. 2 D. 1
6.如图,在菱形ABCD中,,则菱形AB边上的高CE的长
是( )。
A. B. C. 5 D.10
7.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )
A.1 B.2 C. D.
8.如图,在口ABCD中,E是AD的中点,若S□ A B CD =1,则图中阴影部分的面积
为( )
A. B. C. D.
9. 如图:下列条件之一能使口ABCD成为菱形的 ( )
①AC⊥BD ② ∠BAD=900 ③ AB=AD ④ AC=BD
A. ①③ B. ②③ C. ③④ D. ①②③
10. 如图,把△ABC绕点C顺时针旋转某个角度后得到△,若∠A=40°,
∠1=70°,则旋转角等于( )
A.30° B.50° C.70° D.100°
11. 如图,在边长为2的正方形ABCD中,M为AD边的中点,延长MD至点E,使ME=MC,以DE为边做正方形DEFG,点D在边CD上,则DG的长是( )
A. B. C . D.
12. 如图1-6,在ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的
是( )
A. B.
C.四边形AECD是等腰梯形 D.
1
2
3
4
5
6
7
8
9
10
11
12
一.选择题答案:
二、填空题:细心填一填,相信你填得又快又准!
13.已知四边形中,, 添加一个条件: ,可推出该四边形是正方形.
14.如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为20cm,则四边形EFGH的周长是 cm 。
15.如图,菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为 .
16.平面直角坐标系中,△ABC的顶点B(-3,-1),将△ABC绕点O沿顺时针方向旋转90°后,点B的坐标为 。
17.如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的关系是S1 S2
(填“>”或“<”或“=” )
18.如图,若梯形的两底长分别为4cm和9cm,两条对角线长分别为5cm和12cm,则该梯形的面积为 cm2。
三、解答题:用心做一做,培养你的综合运用能力,相信你是最棒的!
19.已知:如图所示的一张矩形纸片(),将纸片折叠一次,使点与重合,再展开,折痕交边于,交边于,分别连结和.
求证:四边形是菱形;
20. 如图,方格纸中的每个小方格都是边长为1个单位的小正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
(1)画出△ABC关于坐标原点成中心对称的△A1B1C1;
(2)将Rt△ABC平移后得到点A2(-3,-4),写出点B2和,C2的坐标;
(3)将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A,B,C,,,试在图上画出Rt△A,B,C,,的图形,并写出各个顶点的坐标。
21.如图,在梯形中,,BD=CD, ∠BDC=900 ,AD=3,BC=8,求的长.
22.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
23.已知:如图,Rt△ABC中,AB=8,BC=10,将△ABC沿着BC方向平移,
(1)若平移的距离为4, 求出四边形ABB/D的面积
(2)若平移的距离为x, 四边形ABB/D的面积为y,列出y与x的函数关系式。
24.在中,,∠ABC=1200,将绕点顺时针旋转角得交于点,分别交于两点.(1)如图1,观察并猜想,在旋转过程中,线段与有怎样的数量关系?并证明你的结论;
(2)如图2,当时,试判断四边形的形状,并说明理由;
同课章节目录
