幻和(课件)-四年级上册数学人教版(共35张PPT)
文档属性
| 名称 | 幻和(课件)-四年级上册数学人教版(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 00:00:00 | ||
图片预览





文档简介
(共35张PPT)
开
课
啦!
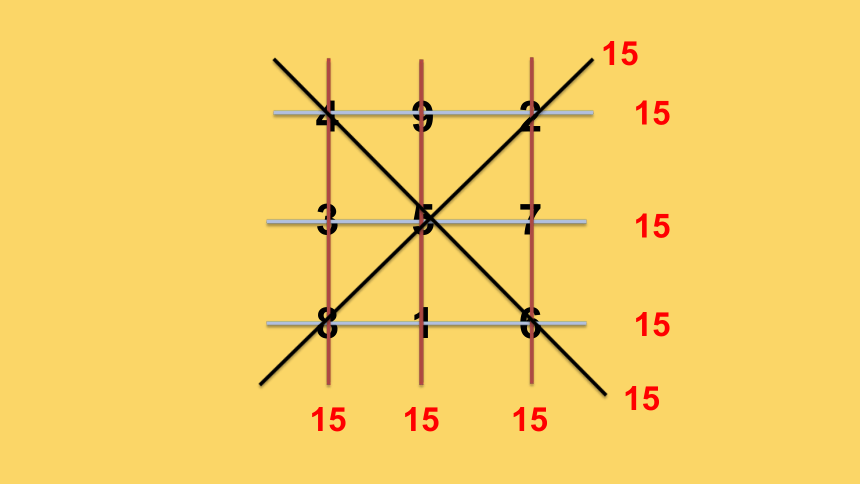
4 9 2
3 5 7
8 1 6
15
15
15
15
15
15
15
15
幻 方
4 9 2
3 5 7
8 1 6
这就是传说中神秘的幻方,这个幻方是
3行3列,所以是三阶幻方,又称为九宫图。
幻方是指横行、竖行、对角线上数的和
都相等的数的方阵。
九宫者,二四为肩,六八为足,左三右七,
戴九履一,五居中央。
幻方中每一行、每一列、每一条对角线上数
的和称为幻和。
5:中间数
我的
发现
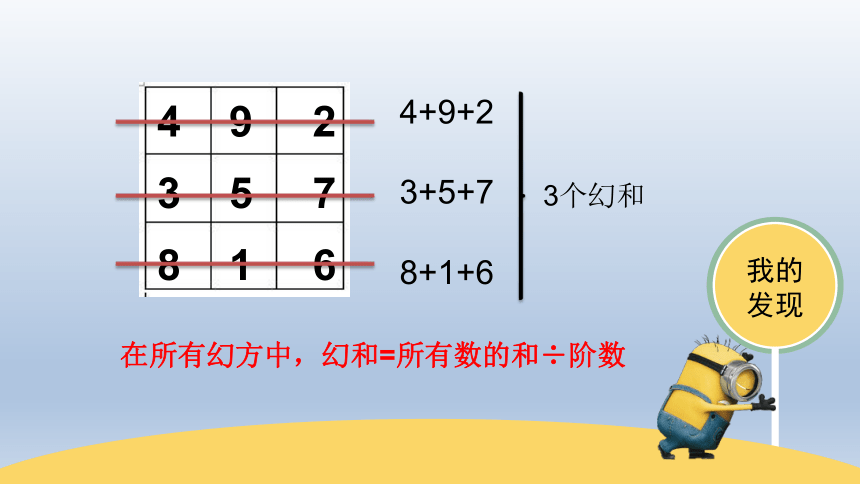
4 9 2
3 5 7
8 1 6
4+9+2
3+5+7
8+1+6
3个幻和
在所有幻方中,幻和=所有数的和÷阶数
a
5+a+ ★ =7+8+ ★
a=10
幻和:6+8+10=24
=24-5-10=9
10
交叉法
5+a=7+8
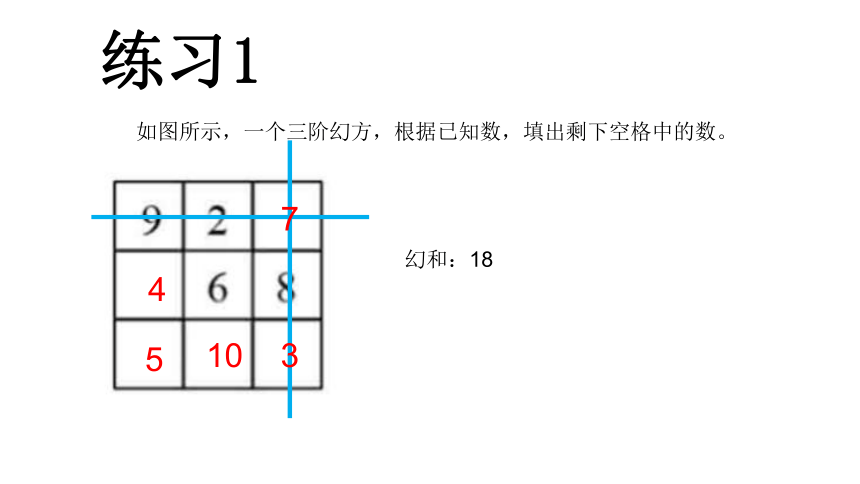
练习1
7
4
5
10
3
幻和:18
如图所示,一个三阶幻方,根据已知数,填出剩下空格中的数。
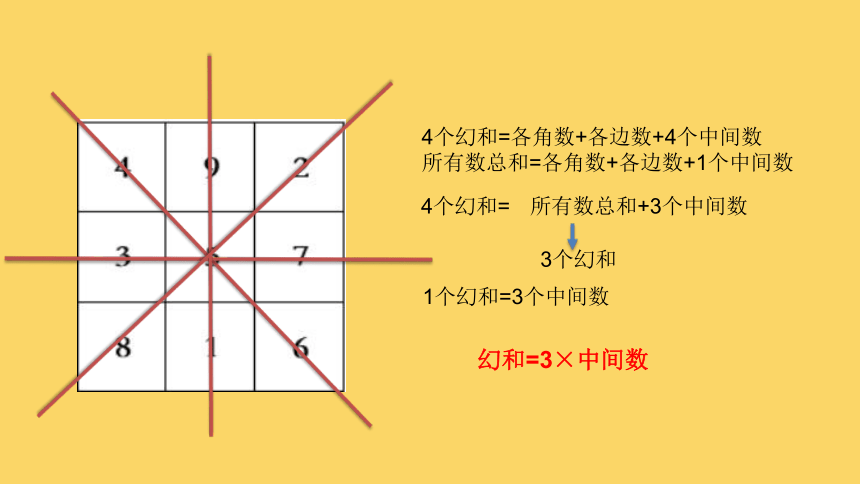
4个幻和=各角数+各边数+4个中间数
所有数总和=各角数+各边数+1个中间数
4个幻和=
所有数总和+3个中间数
3个幻和
1个幻和=3个中间数
幻和=3×中间数
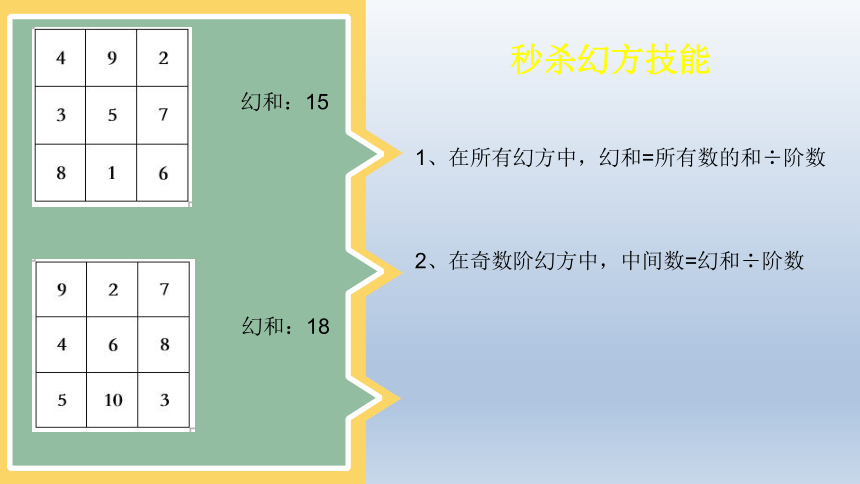
幻和:15
幻和:18
1、在所有幻方中,幻和=所有数的和÷阶数
2、在奇数阶幻方中,中间数=幻和÷阶数
秒杀幻方技能
练习2
11
9
7
8
13
5
12
请在这个未完成的3×3的方格阵中的每个格子内各填上一个不同的数,使得每行、
每列、每条对角线的和都等于27.
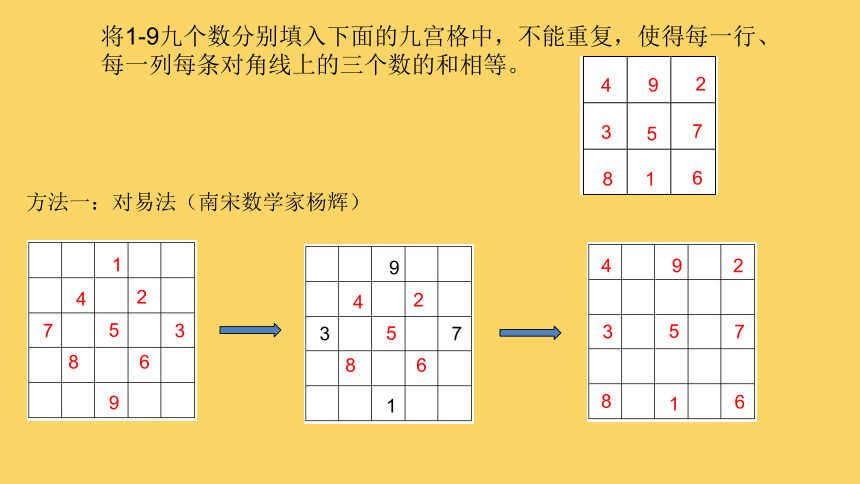
将1-9九个数分别填入下面的九宫格中,不能重复,使得每一行、
每一列每条对角线上的三个数的和相等。
方法一:对易法(南宋数学家杨辉)
1
2
3
4
5
9
6
7
8
9
2
7
4
5
1
6
3
8
9
2
7
4
5
1
6
3
8
4
9
2
7
3
8
1
5
6
将1-9九个数分别填入下面的九宫格中,不能重复,使得每一行、
每一列每条对角线上的三个数的和相等。
方法二:罗伯法(法国数学家罗伯特)
1
2
2
3
3
4
5
6
7
7
7
7
8
8
9
9
8
1
6
3
5
7
4
9
2
我的
发现
1、对易法、罗伯法都只适用于奇数阶的幻方中
2、罗伯法:把1(最小数)填在第一行的正中间
3、每一个数放在前一个数的右上角
4、若所要放的格超出最顶行,
则放在最底行(仍需放在右一列)
5、若所要放的格超出最右列,
则放在最左侧(仍需放在上一行)
6、若所要放的格已经填好其他数,或者同时超
出了最顶格或最右侧,则把它放在前一个数
的下一格。
罗伯法
5
10
15
20
25
30
35
40
45
将5,10,15,20,25,30,35,40,45这九个数分别填入下图,使每行、
每列、两条对角线上三个数的和都相等。
25
5
45
20
10
15
40
30
35
中间数=幻和÷阶数
5-45 10-40 15-35 20-30
将5,10,15,20,25,30,35,40,45这九个数分别填入下图,使每行、
每列、两条对角线上三个数的和都相等。
九宫者,二四为肩,六八为足,左三右七,
戴九履一,五居中央。
25
45
5
40
30
15
20
10
35
将5,10,15,20,25,30,35,40,45这九个数分别填入下图,使每行、
每列、两条对角线上三个数的和都相等。
练习3
14
11
8
在如下的3×3的反格阵中填入缺失的7个数,使得每行、每列、每条对角线上的数
之和都等于42,第二行右边的空格填入的数是多少?
练习4
96
94
100
95
93
98
97
92
99
4
8
5
9
在幻方中,每行、每列和每条对角线上的数之和都是24,那么A+B=( )
练习5
弹弓法
a
b
=(a+b) ÷2
c
=(a+c) ÷2
d
=(c+d) ÷2
=(b+d) ÷2
练习5
(A+7) ÷2=8
A=9
练习6
17
10
12
幻和:17+10+12=39
9
8
13
23
9+15+27=11+A+17
练习7
A=14
幻和:18+6+16+28=68
B=8
练习8
12
10
幻和:15+14+10+23=62
8
16
21
25
9
练习10
总结
1、交叉法
2、对易法
3、罗伯法
4、在所有幻方中,幻和=所有数的和÷阶数
在奇数阶幻方中,中间数=幻和÷阶数
5、弹弓法
补充题一
补充题二
补充题三
本讲巩固
本讲巩固
本讲巩固
开
课
啦!
4 9 2
3 5 7
8 1 6
15
15
15
15
15
15
15
15
幻 方
4 9 2
3 5 7
8 1 6
这就是传说中神秘的幻方,这个幻方是
3行3列,所以是三阶幻方,又称为九宫图。
幻方是指横行、竖行、对角线上数的和
都相等的数的方阵。
九宫者,二四为肩,六八为足,左三右七,
戴九履一,五居中央。
幻方中每一行、每一列、每一条对角线上数
的和称为幻和。
5:中间数
我的
发现
4 9 2
3 5 7
8 1 6
4+9+2
3+5+7
8+1+6
3个幻和
在所有幻方中,幻和=所有数的和÷阶数
a
5+a+ ★ =7+8+ ★
a=10
幻和:6+8+10=24
=24-5-10=9
10
交叉法
5+a=7+8
练习1
7
4
5
10
3
幻和:18
如图所示,一个三阶幻方,根据已知数,填出剩下空格中的数。
4个幻和=各角数+各边数+4个中间数
所有数总和=各角数+各边数+1个中间数
4个幻和=
所有数总和+3个中间数
3个幻和
1个幻和=3个中间数
幻和=3×中间数
幻和:15
幻和:18
1、在所有幻方中,幻和=所有数的和÷阶数
2、在奇数阶幻方中,中间数=幻和÷阶数
秒杀幻方技能
练习2
11
9
7
8
13
5
12
请在这个未完成的3×3的方格阵中的每个格子内各填上一个不同的数,使得每行、
每列、每条对角线的和都等于27.
将1-9九个数分别填入下面的九宫格中,不能重复,使得每一行、
每一列每条对角线上的三个数的和相等。
方法一:对易法(南宋数学家杨辉)
1
2
3
4
5
9
6
7
8
9
2
7
4
5
1
6
3
8
9
2
7
4
5
1
6
3
8
4
9
2
7
3
8
1
5
6
将1-9九个数分别填入下面的九宫格中,不能重复,使得每一行、
每一列每条对角线上的三个数的和相等。
方法二:罗伯法(法国数学家罗伯特)
1
2
2
3
3
4
5
6
7
7
7
7
8
8
9
9
8
1
6
3
5
7
4
9
2
我的
发现
1、对易法、罗伯法都只适用于奇数阶的幻方中
2、罗伯法:把1(最小数)填在第一行的正中间
3、每一个数放在前一个数的右上角
4、若所要放的格超出最顶行,
则放在最底行(仍需放在右一列)
5、若所要放的格超出最右列,
则放在最左侧(仍需放在上一行)
6、若所要放的格已经填好其他数,或者同时超
出了最顶格或最右侧,则把它放在前一个数
的下一格。
罗伯法
5
10
15
20
25
30
35
40
45
将5,10,15,20,25,30,35,40,45这九个数分别填入下图,使每行、
每列、两条对角线上三个数的和都相等。
25
5
45
20
10
15
40
30
35
中间数=幻和÷阶数
5-45 10-40 15-35 20-30
将5,10,15,20,25,30,35,40,45这九个数分别填入下图,使每行、
每列、两条对角线上三个数的和都相等。
九宫者,二四为肩,六八为足,左三右七,
戴九履一,五居中央。
25
45
5
40
30
15
20
10
35
将5,10,15,20,25,30,35,40,45这九个数分别填入下图,使每行、
每列、两条对角线上三个数的和都相等。
练习3
14
11
8
在如下的3×3的反格阵中填入缺失的7个数,使得每行、每列、每条对角线上的数
之和都等于42,第二行右边的空格填入的数是多少?
练习4
96
94
100
95
93
98
97
92
99
4
8
5
9
在幻方中,每行、每列和每条对角线上的数之和都是24,那么A+B=( )
练习5
弹弓法
a
b
=(a+b) ÷2
c
=(a+c) ÷2
d
=(c+d) ÷2
=(b+d) ÷2
练习5
(A+7) ÷2=8
A=9
练习6
17
10
12
幻和:17+10+12=39
9
8
13
23
9+15+27=11+A+17
练习7
A=14
幻和:18+6+16+28=68
B=8
练习8
12
10
幻和:15+14+10+23=62
8
16
21
25
9
练习10
总结
1、交叉法
2、对易法
3、罗伯法
4、在所有幻方中,幻和=所有数的和÷阶数
在奇数阶幻方中,中间数=幻和÷阶数
5、弹弓法
补充题一
补充题二
补充题三
本讲巩固
本讲巩固
本讲巩固
