沪科版数学七年级下册 6.1 平方根、立立根第1课时 课件 2021—2022学年 (共20张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 6.1 平方根、立立根第1课时 课件 2021—2022学年 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 21:27:08 | ||
图片预览






文档简介
(共20张PPT)
6.1平方根
第1课时
学习目标
1. 了解平方根、算术平方根的概念,会用根号表示一个数的平方根、算术平方根;
平方根
2.了解开方与乘方是互逆运算,会利用这种互逆关系求百以内整数的平方根、算术平方根,会进行简单的开平方运算;
3.通过探索平方根与算术平方根的区别与联系,学会利用算术平方根解决平方根的问题;
4.通过对平方根的学习,培养学生从多方面、多角度分析解决问题的思想意识,养成全面分析问题的习惯.
重点
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
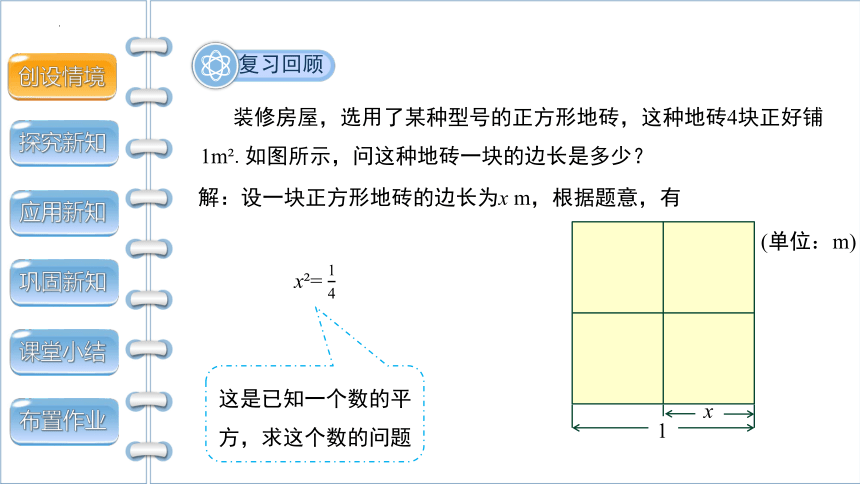
装修房屋,选用了某种型号的正方形地砖,这种地砖4块正好铺1m .如图所示,问这种地砖一块的边长是多少?
1
x
(单位:m)
解:设一块正方形地砖的边长为x m,根据题意,有
x =
这是已知一个数的平方,求这个数的问题
如果一个数的平方等于 ,这个数是多少?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
答:或
由于( ) =,那么这个数也可以是
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
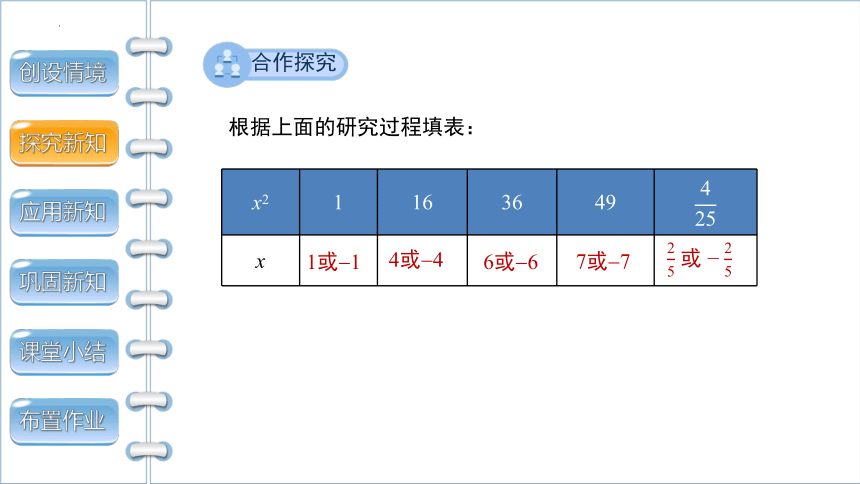
根据上面的研究过程填表:
x2 1 16 36 49
x
1或 1
4或 4
6或 6
7或 7
或
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根或二次方根.这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
例如,由于10 =100,( 10) =100,所以100的平方根是10和 10.
注意:一个正数有两个平方根,不要丢掉负的平方根.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
交流
16的平方根是什么?
0的平方根是什么?
9有没有平方根?
49的平方根是7,是否正确?
2是4的一个平方根,是否正确?
±4
0
没有
巩固新知
课堂小结
布置作业
创设情境
想一想
1.正数有两个平方根,它们互为相反数.
2. 0 的平方根还是0.
3. 负数没有平方根.
正数的平方根有什么特点?0 的平方根是多少?负数有平方根吗?
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
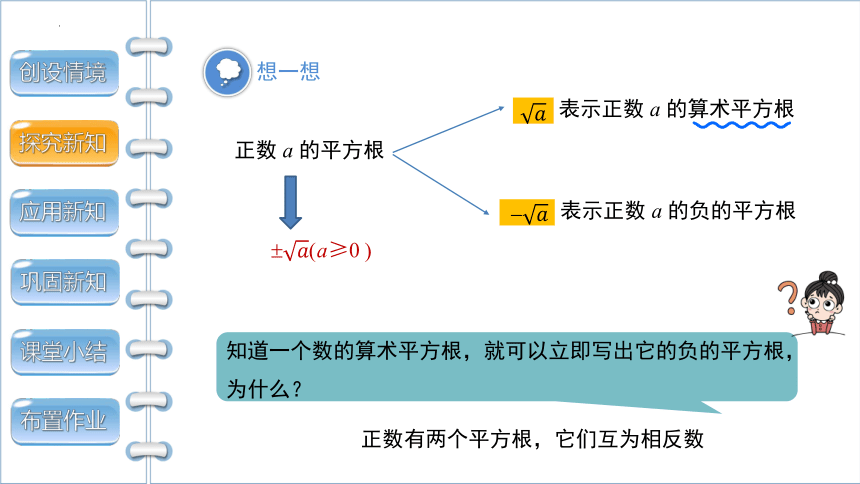
正数 a 的平方根
表示正数 a 的算术平方根
表示正数 a 的负的平方根
a≥0
知道一个数的算术平方根,就可以立即写出它的负的平方根,
为什么?
正数有两个平方根,它们互为相反数
想一想
应用新知
探究新知
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
1
4
9
已知一个数,求它的平方的运算,叫做平方运算.
+1
1
+2
2
+3
3
平方
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
1
4
9
+1
1
+2
2
+3
3
反之,已知一个数的平方,求这个数的运算叫什么?
求一个数的平方根的运算,叫做开平方.平方与开平方互为逆运算.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
例1 判断下列各数是否有平方根,为什么?
(1) 25 ; (2) ; (3) 0.0169; (4) 64
解:(1)因为正数和零都有平方根,负数没有平方根,所以25,, 0.0169都有平方根; 64 没有平方根.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
例2 求下列各数的平方根和算术平方根:
(1) ; (2) ; (3) ; (4) ( 3)
解:(1) 因为( 1) 1,所以1的平方根是 1,即 1;1的算术平方根是1.
解:(2) 因为( 9) 81,所以81的平方根是 9,即 9;81的算术平方根是9.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
解:(4) 因为( 3) 9,所以9的平方根是 3,也就是( 3) 的平方根是 3,即 3;( 3) 的算术平方根是3.
解:(3) 因为( 8) 64,所以64的平方根是 8,即 8;64的算术平方根是8.
例2 求下列各数的平方根和算术平方根:
(3) (4) ( 3)
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
归纳
你能总结一下平方根与算术平方根的概念的区别与联系吗?
区别:正数的平方根有两个,而它的算术平方根只有一个;
联系:正数的两个平方根中正的那个平方根就是它的算术平方根,0的平方根就是它的算术平方根.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.判断是非:
(1)4是16的算术平方根.
(2)是的一个平方根.
(3)( 5) 的平方根是 5.
(4)0的算术平方根是0.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.下列各式是否有意义,说明理由:
(1).
(2).
(3).
(4).
有
有
有
无
被开方数为3>0,因此有意义;
被开方数为 3<0,因此无意义;
被开方数为( 3) >0,因此有意义;
被开方数为0,因此有意义.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
概念:
平方根
性质:
正数有两个平方根,两个平方根互为相反数.
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根或二次方根.这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
0 的平方根还是0.
负数没有平方根.
布置作业
教科书第5页练习第1,4题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
6.1平方根
第1课时
学习目标
1. 了解平方根、算术平方根的概念,会用根号表示一个数的平方根、算术平方根;
平方根
2.了解开方与乘方是互逆运算,会利用这种互逆关系求百以内整数的平方根、算术平方根,会进行简单的开平方运算;
3.通过探索平方根与算术平方根的区别与联系,学会利用算术平方根解决平方根的问题;
4.通过对平方根的学习,培养学生从多方面、多角度分析解决问题的思想意识,养成全面分析问题的习惯.
重点
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
装修房屋,选用了某种型号的正方形地砖,这种地砖4块正好铺1m .如图所示,问这种地砖一块的边长是多少?
1
x
(单位:m)
解:设一块正方形地砖的边长为x m,根据题意,有
x =
这是已知一个数的平方,求这个数的问题
如果一个数的平方等于 ,这个数是多少?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
答:或
由于( ) =,那么这个数也可以是
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
根据上面的研究过程填表:
x2 1 16 36 49
x
1或 1
4或 4
6或 6
7或 7
或
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根或二次方根.这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
例如,由于10 =100,( 10) =100,所以100的平方根是10和 10.
注意:一个正数有两个平方根,不要丢掉负的平方根.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
交流
16的平方根是什么?
0的平方根是什么?
9有没有平方根?
49的平方根是7,是否正确?
2是4的一个平方根,是否正确?
±4
0
没有
巩固新知
课堂小结
布置作业
创设情境
想一想
1.正数有两个平方根,它们互为相反数.
2. 0 的平方根还是0.
3. 负数没有平方根.
正数的平方根有什么特点?0 的平方根是多少?负数有平方根吗?
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
正数 a 的平方根
表示正数 a 的算术平方根
表示正数 a 的负的平方根
a≥0
知道一个数的算术平方根,就可以立即写出它的负的平方根,
为什么?
正数有两个平方根,它们互为相反数
想一想
应用新知
探究新知
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
1
4
9
已知一个数,求它的平方的运算,叫做平方运算.
+1
1
+2
2
+3
3
平方
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
1
4
9
+1
1
+2
2
+3
3
反之,已知一个数的平方,求这个数的运算叫什么?
求一个数的平方根的运算,叫做开平方.平方与开平方互为逆运算.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
例1 判断下列各数是否有平方根,为什么?
(1) 25 ; (2) ; (3) 0.0169; (4) 64
解:(1)因为正数和零都有平方根,负数没有平方根,所以25,, 0.0169都有平方根; 64 没有平方根.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
例2 求下列各数的平方根和算术平方根:
(1) ; (2) ; (3) ; (4) ( 3)
解:(1) 因为( 1) 1,所以1的平方根是 1,即 1;1的算术平方根是1.
解:(2) 因为( 9) 81,所以81的平方根是 9,即 9;81的算术平方根是9.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
解:(4) 因为( 3) 9,所以9的平方根是 3,也就是( 3) 的平方根是 3,即 3;( 3) 的算术平方根是3.
解:(3) 因为( 8) 64,所以64的平方根是 8,即 8;64的算术平方根是8.
例2 求下列各数的平方根和算术平方根:
(3) (4) ( 3)
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
归纳
你能总结一下平方根与算术平方根的概念的区别与联系吗?
区别:正数的平方根有两个,而它的算术平方根只有一个;
联系:正数的两个平方根中正的那个平方根就是它的算术平方根,0的平方根就是它的算术平方根.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.判断是非:
(1)4是16的算术平方根.
(2)是的一个平方根.
(3)( 5) 的平方根是 5.
(4)0的算术平方根是0.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.下列各式是否有意义,说明理由:
(1).
(2).
(3).
(4).
有
有
有
无
被开方数为3>0,因此有意义;
被开方数为 3<0,因此无意义;
被开方数为( 3) >0,因此有意义;
被开方数为0,因此有意义.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
概念:
平方根
性质:
正数有两个平方根,两个平方根互为相反数.
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根或二次方根.这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
0 的平方根还是0.
负数没有平方根.
布置作业
教科书第5页练习第1,4题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
