北师大版小学数学六年级上册6. 《比的认识—— 整理与复习》 课件(共18张PPT)
文档属性
| 名称 | 北师大版小学数学六年级上册6. 《比的认识—— 整理与复习》 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 531.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 19:32:00 | ||
图片预览





文档简介
(共18张PPT)
第六单元 比的认识
整理与复习
一、复习回顾
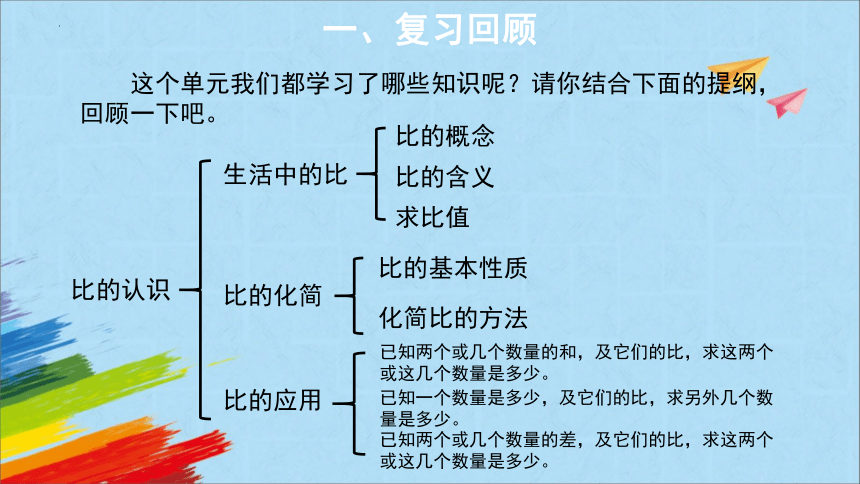
这个单元我们都学习了哪些知识呢?请你结合下面的提纲,回顾一下吧。
比的认识
比的化简
生活中的比
比的概念
已知两个或几个数量的和,及它们的比,求这两个或这几个数量是多少。
比的基本性质
比的应用
比的含义
求比值
化简比的方法
已知一个数量是多少,及它们的比,求另外几个数量是多少。
已知两个或几个数量的差,及它们的比,求这两个或这几个数量是多少。
一、复习回顾
比的概念:两个数相除又叫作两个数的比,“∶”是比号。比的前项除以后项所得的商,叫作比值。
比的含义:比表示两个或几个数量之间的关系。
求比值:用比的前项除以比的后项。最后结果是数值。
比值通常用分数、小数和整数表示。
生活中的比
比的基本性质:比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变。
比的化简
一、复习回顾
比的化简
一、复习回顾
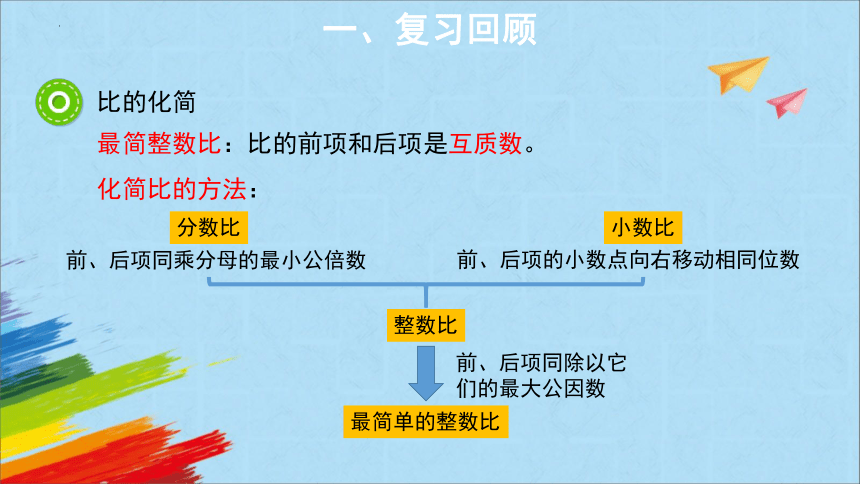
最简整数比:比的前项和后项是互质数。
化简比的方法:
分数比
小数比
整数比
最简单的整数比
前、后项同除以它们的最大公因数
前、后项同乘分母的最小公倍数
前、后项的小数点向右移动相同位数
一、复习回顾
比的应用
1.已知两个或几个数量的和,及它们的比,求这两个或这几个数量是多少。
2.已知一个数量是多少,及它们的比,求另外几个数量是多少。
3.已知两个或几个数量的差,及它们的比,求这两个或这几个数量是多少。
二、基础练习
1.把下面各题中的数量关系写成比,并求出比值。
(1)小小试验田今年种了2 公顷小麦,共收了6 吨,总产量与公顷数的比是 ,比值是 。
(2)跑36 km大约需要2 时,路程与时间的比大约是 ,比值是 ,这个比值表示的是 。
(3)买6 m装饰布做窗帘,付款72 元。付的钱数与买的米数的比是 ,比值是 ,这个比值表示的是 。
3:1
3
18
18:1
速度
12:1
12
单价
二、基础练习
2.大齿轮有100个齿,每分转25转;小齿轮有25个齿,每分转100转。
1
4
(1)大齿轮和小齿轮齿数的比是 ,比值是 。
(2)大齿轮和小齿轮每分转数的比是 ,比值是 。
4∶1
4
1∶4
二、基础练习
3.大正方形边长是4 cm,小正方形边长是3 cm。
(1)大、小正方形边长的比是 ,比值是 。
(2)大、小正方形周长的比是 ,比值是 。
(3)大、小正方形面积的比是 ,比值是 。
4:3
4:3
16:9
4
3
4
3
16
9
二、基础练习
24:32 56:14 15:25
4.求比值。
5.化简比。
8:36 4:0.8 4厘米∶32米
二、基础练习
三、强化练习
(1)比的前项和后项同时乘或除以同一个数,比值不变。 ( )
(2)把5∶9的前项和后项同时加上7,比值不变。 ( )
(3)一个三角形三个内角度数比是1∶2∶3,这个三角形一定是直角三角形。
( )
(4)小强的身高是二米,妈妈的身高是158厘米,那小强和妈妈的身高比是2∶158。 ( )
(5)两个大小不同的圆的半径比是1∶3,那么它们的面积比也是1∶3。 ( )
×
√
×
×
×
1.判断题。
三、强化练习
2.体育室有60根跳绳,按人数分配给甲、乙两班。甲班有42人,乙班有48人,两个班各分得跳绳多少根
答:甲班分得跳绳28根,乙班分得跳绳32 根。
60÷(7+8)=4(根)
甲班:4×7=28(根)
乙班:4×8=32(根)
三、强化练习
3.六(3)班男、女生人数的比是5∶3,已知男生比女生多14人,男、女生各有多少人
男:7×5=35(人)
答:男生有35人,女生有21人。
5-3=2
14÷2=7(人)
女:7×3=21(人)
三、强化练习
4.一种混凝土的水泥、沙子、石子的质量比是2∶3 ∶ 5,要配制20吨混凝土,需要水泥、沙子、石子各多少吨
2+3+5=10
答:需要水泥4吨、沙子6吨、石子10吨。
20÷10=2(吨)
水泥:2×2=4(吨)
沙子:2×3=6(吨)
石子:2×5=10(吨)
四、拓展练习
1.每个大花篮里有玫瑰花40朵,百合花30朵。每个大花篮的花是按怎样的比搭配的?花店进来一大批花,按这样的比可以怎样搭配?填一填。
玫瑰花 百合花
80朵
120朵
玫瑰花∶百合花
= 40∶30
= 4 ∶ 3
百合花:80÷4×3=60(朵)
60朵
玫瑰花:120÷3×4=160(朵)
160朵
200朵
百合花:200÷4×3=150(朵)
150朵
四、拓展练习
2.甲、乙、丙三个数的比是1∶2∶3,如果它们的平均数是30,那么甲数是多少。
甲数是15。
再见
第六单元 比的认识
整理与复习
一、复习回顾
这个单元我们都学习了哪些知识呢?请你结合下面的提纲,回顾一下吧。
比的认识
比的化简
生活中的比
比的概念
已知两个或几个数量的和,及它们的比,求这两个或这几个数量是多少。
比的基本性质
比的应用
比的含义
求比值
化简比的方法
已知一个数量是多少,及它们的比,求另外几个数量是多少。
已知两个或几个数量的差,及它们的比,求这两个或这几个数量是多少。
一、复习回顾
比的概念:两个数相除又叫作两个数的比,“∶”是比号。比的前项除以后项所得的商,叫作比值。
比的含义:比表示两个或几个数量之间的关系。
求比值:用比的前项除以比的后项。最后结果是数值。
比值通常用分数、小数和整数表示。
生活中的比
比的基本性质:比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变。
比的化简
一、复习回顾
比的化简
一、复习回顾
最简整数比:比的前项和后项是互质数。
化简比的方法:
分数比
小数比
整数比
最简单的整数比
前、后项同除以它们的最大公因数
前、后项同乘分母的最小公倍数
前、后项的小数点向右移动相同位数
一、复习回顾
比的应用
1.已知两个或几个数量的和,及它们的比,求这两个或这几个数量是多少。
2.已知一个数量是多少,及它们的比,求另外几个数量是多少。
3.已知两个或几个数量的差,及它们的比,求这两个或这几个数量是多少。
二、基础练习
1.把下面各题中的数量关系写成比,并求出比值。
(1)小小试验田今年种了2 公顷小麦,共收了6 吨,总产量与公顷数的比是 ,比值是 。
(2)跑36 km大约需要2 时,路程与时间的比大约是 ,比值是 ,这个比值表示的是 。
(3)买6 m装饰布做窗帘,付款72 元。付的钱数与买的米数的比是 ,比值是 ,这个比值表示的是 。
3:1
3
18
18:1
速度
12:1
12
单价
二、基础练习
2.大齿轮有100个齿,每分转25转;小齿轮有25个齿,每分转100转。
1
4
(1)大齿轮和小齿轮齿数的比是 ,比值是 。
(2)大齿轮和小齿轮每分转数的比是 ,比值是 。
4∶1
4
1∶4
二、基础练习
3.大正方形边长是4 cm,小正方形边长是3 cm。
(1)大、小正方形边长的比是 ,比值是 。
(2)大、小正方形周长的比是 ,比值是 。
(3)大、小正方形面积的比是 ,比值是 。
4:3
4:3
16:9
4
3
4
3
16
9
二、基础练习
24:32 56:14 15:25
4.求比值。
5.化简比。
8:36 4:0.8 4厘米∶32米
二、基础练习
三、强化练习
(1)比的前项和后项同时乘或除以同一个数,比值不变。 ( )
(2)把5∶9的前项和后项同时加上7,比值不变。 ( )
(3)一个三角形三个内角度数比是1∶2∶3,这个三角形一定是直角三角形。
( )
(4)小强的身高是二米,妈妈的身高是158厘米,那小强和妈妈的身高比是2∶158。 ( )
(5)两个大小不同的圆的半径比是1∶3,那么它们的面积比也是1∶3。 ( )
×
√
×
×
×
1.判断题。
三、强化练习
2.体育室有60根跳绳,按人数分配给甲、乙两班。甲班有42人,乙班有48人,两个班各分得跳绳多少根
答:甲班分得跳绳28根,乙班分得跳绳32 根。
60÷(7+8)=4(根)
甲班:4×7=28(根)
乙班:4×8=32(根)
三、强化练习
3.六(3)班男、女生人数的比是5∶3,已知男生比女生多14人,男、女生各有多少人
男:7×5=35(人)
答:男生有35人,女生有21人。
5-3=2
14÷2=7(人)
女:7×3=21(人)
三、强化练习
4.一种混凝土的水泥、沙子、石子的质量比是2∶3 ∶ 5,要配制20吨混凝土,需要水泥、沙子、石子各多少吨
2+3+5=10
答:需要水泥4吨、沙子6吨、石子10吨。
20÷10=2(吨)
水泥:2×2=4(吨)
沙子:2×3=6(吨)
石子:2×5=10(吨)
四、拓展练习
1.每个大花篮里有玫瑰花40朵,百合花30朵。每个大花篮的花是按怎样的比搭配的?花店进来一大批花,按这样的比可以怎样搭配?填一填。
玫瑰花 百合花
80朵
120朵
玫瑰花∶百合花
= 40∶30
= 4 ∶ 3
百合花:80÷4×3=60(朵)
60朵
玫瑰花:120÷3×4=160(朵)
160朵
200朵
百合花:200÷4×3=150(朵)
150朵
四、拓展练习
2.甲、乙、丙三个数的比是1∶2∶3,如果它们的平均数是30,那么甲数是多少。
甲数是15。
再见
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
