第二章有理数及其计算（复习）

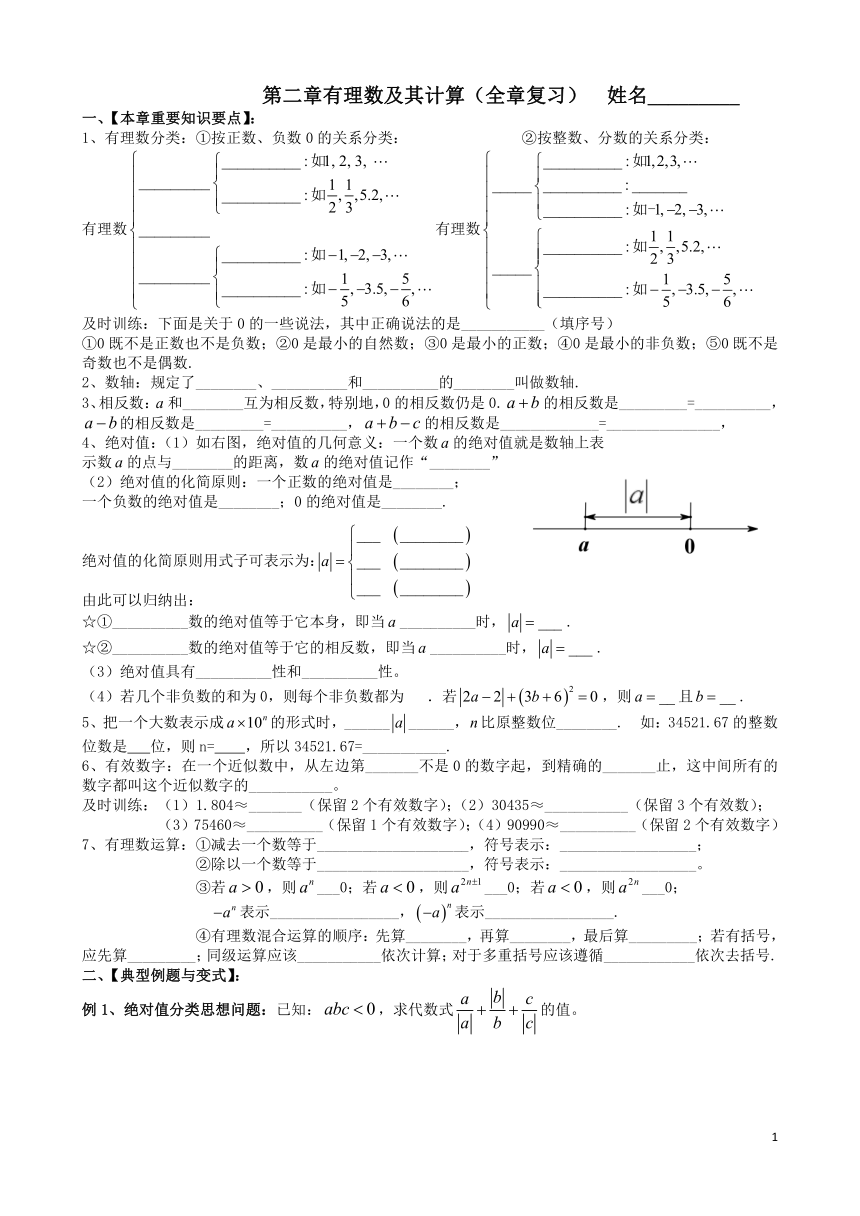
第二章有理数及其计算（全章复习） 姓名_________
一、【本章重要知识要点】：
1、有理数分类：①按正数、负数0的关系分类： ②按整数、分数的关系分类：
有理数有理数
及时训练：下面是关于0的一些说法，其中正确说法的是___________（填序号）
①0既不是正数也不是负数；②0是最小的自然数；③0是最小的正数；④0是最小的非负数；⑤0既不是奇数也不是偶数.
2、数轴：规定了________、__________和__________的________叫做数轴.
3、相反数：和________互为相反数，特别地，0的相反数仍是0.的相反数是_________=__________，的相反数是_________=__________，的相反数是_____________=_______________，
4、绝对值：（1）如右图，绝对值的几何意义：一个数的绝对值就是数轴上表
示数的点与________的距离，数的绝对值记作“________”
（2）绝对值的化简原则：一个正数的绝对值是________；
一个负数的绝对值是________；0的绝对值是________.
绝对值的化简原则用式子可表示为：
由此可以归纳出：
☆①__________数的绝对值等于它本身，即当__________时，.
☆②__________数的绝对值等于它的相反数，即当__________时，.
（3）绝对值具有__________性和__________性。
（4）若几个非负数的和为0，则每个非负数都为 ．若，则且.
5、把一个大数表示成的形式时，____________，比原整数位________. 如：34521.67的整数位数是 位，则n= ，所以34521.67=___________.
6、有效数字：在一个近似数中，从左边第_______不是0的数字起，到精确的_______止，这中间所有的数字都叫这个近似数字的___________。
及时训练：（1）1.804≈_______（保留2个有效数字）；（2）30435≈___________（保留3个有效数）；
（3）75460≈__________（保留1个有效数字）；（4）90990≈__________（保留2个有效数字）
7、有理数运算：①减去一个数等于____________________，符号表示：__________________；
②除以一个数等于____________________，符号表示：__________________。
③若，则___0；若，则___0；若，则___0；
表示_________________，表示_________________.
④有理数混合运算的顺序：先算________，再算________，最后算_________；若有括号，应先算_________；同级运算应该___________依次计算；对于多重括号应该遵循____________依次去括号.
二、【典型例题与变式】：
例1、绝对值分类思想问题：已知：，求代数式的值。
变式训练：求代数式的值。
例2、混合运算：
变式训练：（1） （2）
例3、有理数的简便计算：
变式训练：（1） （2）
例4、定义新运算：(1)用“*”代表一种运算，，求的值；
（2）现在定义两种计算“”和“”，对于任意两个整数a、b，，，求的值.
变式训练：
(1) 已知x、y为有理数，若规定一种新运算符号“”，定义，请根据运算符号“”的意义完成下列各题：（1）35； （2）
(2) 在实数的原有运算法则中我们补充定义新运算“”如下：
当a≥b时，；当a＜b时，．
则当x＝2时，的值为 (“· ”和“－”仍为实数运算中的乘号和减号)．
三、【强化训练与提高】：
一、选择题：
1．下列说法错误的是（ ）
A．数轴上，原点位置的确定是任意的 B．数轴上，单位长度是固定不变的
C．数轴上，单位长度1的长度的确定，可根据需要任意选取 D．数轴上的两个方向均可以无限延长
2．下列说法错误的是（ ）
A．互为相反数的两个数的绝对值相等 B．任何有理数的绝对值都是正数
C．两个不相等的数，它们的绝对值可能相等 D．任何数的绝对值都不是负数
3．若是有理数，则的值是（ ）
A．可能是负数 B．不可能是负数 C．必为正数 D．可能正数也可能负数
4．下列说法正确的有（ ）
①若，则；②若，则；③若，则；④若，则.
A．1个 B．2个 C．3个 D．4个
5．下列判断中，正确的是（ ）
A．若，则 B．若，则 C．若，则 D．若，则
6．下列判断中，正确的是（ ）
A．若，则 B．若，则
C．若，则 D．若为任意有理数，则≤0
二、填空题：
1．的相反数是______、 倒数是_____； 的绝对值是_______。
2. 在数轴上距离原点4个单位的点对应的数是___________；
在数轴上距离-4所表示的点5个单位的点对应的数是___________；
已知点A在数轴上对应有理数，将点A向左移动4个单位长度后，再向右移1个单位长度后得到点B，点B对应的有理数是.5，则=___________。
3. 绝对值不大于3的自然数有_____________；绝对值小于4的负整数有_______________；
绝对值小于100的所有整数的积是__________、和是__________。
4．若，则x与y的关系是__________；若，则，则x与y的关系是__________；
若则x=________；若则x=________。
5．已知　＋（n＋２）2＝０，则nm的值为 ；
如果∣∣与()互为相反数，那么的值是_________。
6. 用“小于”号比较大小：：____________________________。
7. 若规定a*b为一种新运算，且a*b＝ab－（a+b），则（－3）*2＝_______。
8. 计算=_________；（-2）2008+（-2）2007= 。
9. 已知a与b互为倒数，m与n互为相反数，x的绝对值为3，则_______；
10. ___________；如上图：则化简：=_____, =_____, =_____；若a<0，则 a与它的相反数的差的绝对值是_____________。
11．若，，则，则___________。
12. 计算：1－2＋3－4＋5－6＋…＋99－100＝____ _；
计算：=_________。
13.当x=___时，有最___值是_____;当x=____时，有最___值是______。
14.已知点4和点9之间的距离为5个单位，有这样的关系，那么点10和点之间的距离是____________；点m和点n（数n比m大）之间的距离是____________；点A、B在数轴上分别表示数a、b，点B在点A的右边,A、B两点间的距离表示为.则=_______；如果数轴上表示和1的两点间距离是2，则__________。
15.“二十四点”的游戏：从扑克牌中抽取黑桃Q、红桃Q、梅花3、方块A，将牌面上的数字（每个数用且只能用一次）进行加减乘除四则运算，使其结果等于24。若红色牌代表负数，黑色牌代表负数，使其结果等于24。运算式子为 。
16.已知整数a、b、c、d满足abcd＝25,且a＞b＞c＞d，则　等于 。
17.若则_______； 若则b_______；若则_______。
18.相反数等于本身的数有______；倒数等于本身的数有______；立方等于本身的数有______；平方等于本身的数有______；绝对值等于本身的数有______；相反数等于它的相反数的数有______；若有理数a的平方与立方相等，则a=___________。
19.某种细胞半个小时便由1个细胞分裂成2个，经过5个小时后，这种细胞能由1个分裂成_______各细胞；n个小时这种细胞能由1个分裂成_______各细胞。
20.的个位数字是______________。
三、解答题：
21.计算：（1）； （2）；
（3）； （4）；
（5）； （6）；
（7）； （8）；
（9）； （10）.
22. 三个互不相等的有理数既可表示为1，，的形式，又可表示为0，，的形式，
试求、的值.
23. 求的所有可能的值.