2022_2023学年湘教版七年级数学上册第四章图形的认识复习课课件(共45张PPT)
文档属性
| 名称 | 2022_2023学年湘教版七年级数学上册第四章图形的认识复习课课件(共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 824.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-01 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
第四章 图形的认识
第四章 复习课
1.知道几何图形包括平面图形与立体图形,能说出常见的立体图形和平面图形的名称.
2.知道线段、射线、直线和角的表示方法,会进行的度、分、秒的换算;会作一条线段等于已知线段.
3.知道线段中点及角平分线的含义,会进行相关的计算.
4.熟记两个基本事实,并能应用它们解决实际问题.
◎重点:线段中点、角平分线的概念,线段和角的有关计算.
◎难点:熟练地进行线段和角的计算.
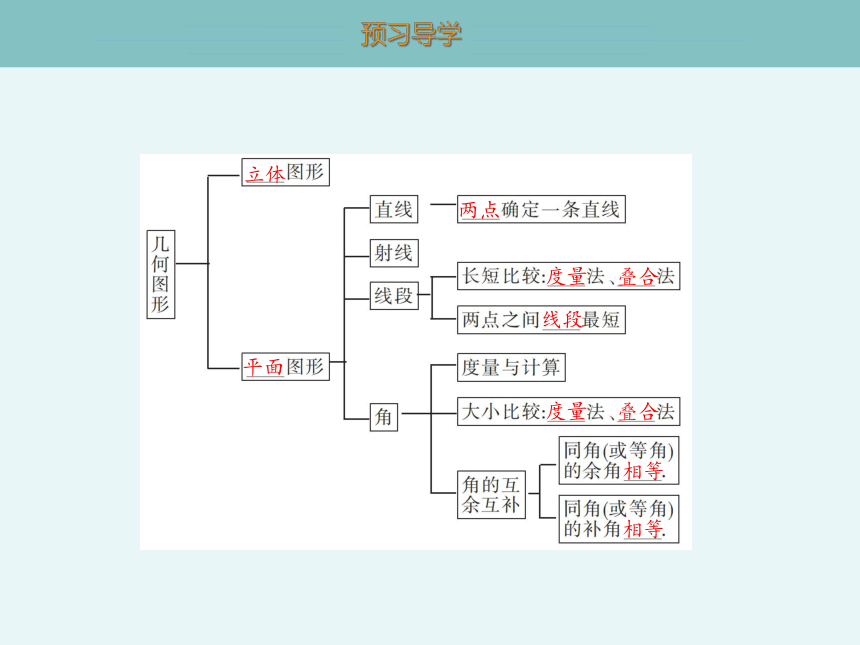
在这一章中,我们学习了哪些知识?你能用知识框图表示本章所学内容吗?
立体
平面
两点
度量
线段
度量
叠合
相等
相等
叠合
1.点与直线的位置关系有: 点在直线上(直线经过点) 、 点在直线外(直线不经过点) .
2.如图,若点B是线段AC的中点,则 AB = BC = AC .
点在直线上(直线经过点)
点在直线外(直线不经过点)
AB
BC
AC
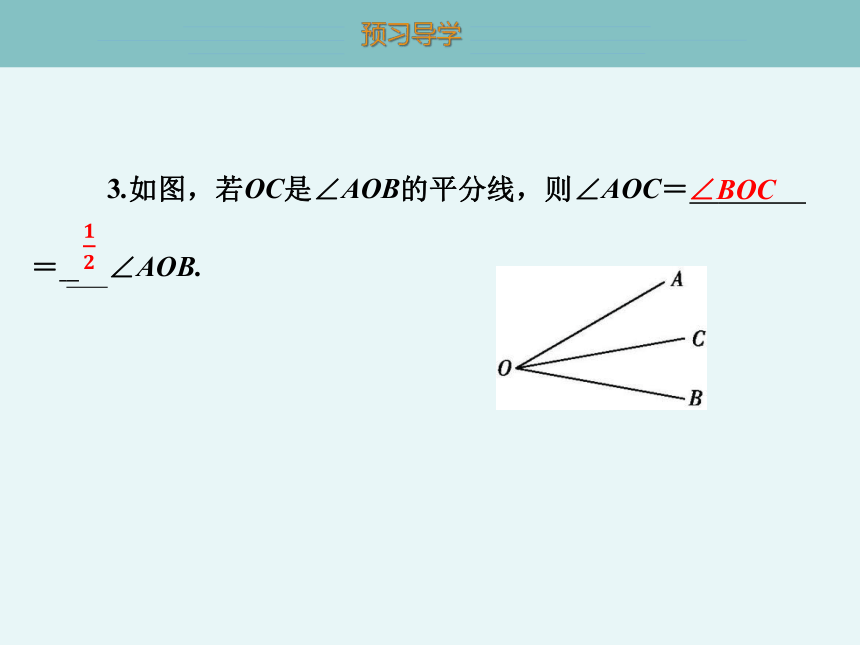
3.如图,若OC是∠AOB的平分线,则∠AOC= ∠BOC = ∠AOB.
∠BOC
4.1°= 60 '= 3600 ″;1'= 60 ″;
1'=°;1″='.
5.若∠A与∠B互余,则∠A+∠B= 90° ;若∠A与∠C互补,则∠A+∠C= 180° .
60
3600
60
90°
180°
立体图形与平面图形
1.在圆、正方形、圆锥、长方体、线段、球、三棱柱、直角三角形中,是立体图形的有 圆锥、长方体、球、三棱柱 ,是平面图形的有 圆、正方形、线段、直角三角形 .
圆锥、长方体、球、三棱柱
圆、正方形、线段、直角三角形
2.下列说法:①射线AB与射线BA表示的是同一条射线;②线段AB与线段BA表示的不是同一条线段;③直线AB与直线BA表示的是同一条直线;④线段、射线都是直线的一部分.其中,正确的是 ③④ .(填序号)
③④
直线、射线、线段
3.“把弯曲的公路改直,就能缩短路程”,其中蕴含的数学道理是 ( D )
A.两点确定一条直线
B.直线比曲线短
C.两点之间直线最短
D.两点之间线段最短
4.如图,可以用字母表示出来的不同线段有 10 条.
D
10
变式训练 (1)往返于A,B两个城市的客车,中途有三个停靠点,该客车有 10 种不同的票价,该客车上要准备 20 种车票.
(2)有5个人,每两个人握一次手一共要握 10 次手.
10
20
10
方法归纳交流 线段的总条数N与线段上的已知点数n的关系是 N= .
N=
数几何图形的个数
如图,回答下列问题:
(1)图中有几条直线?能用字母表示出来的有哪些?
(2)图中有几条射线?用字母表示出来.
(3)图中有几条线段?用字母表示出来.
解:(1)图中有1条直线,表示为直线AD(或直线AB、AC、BD、BC、CD).
(2)共有8条射线,能用字母表示的有射线AB、BA、BC、CB、CD、DC.
(3)共有6条线段,表示为线段AB、AC、AD、BC、BD、CD.
5.如图,有四个点A、B、C、D,按照下列语句画出图形:
(1)画直线AB;
(2)画射线BD;
(3)作线段BC,并以厘米为单位,度量其长度;
(4)线段AC和线段BD相交于点O;
(5)反向延长线段BC至点E,使BE=BC.
解:如图.BC=0.6 cm.
6.已知线段AB=24 cm,点C是线段AB的中点,点D是CB的中点,点E在线段AC上,且CE=AC.画图并计算ED的长.
解:如图,因为点C是AB的中点,AB=24 cm,所以AC=CB=AB=12 cm.
线段的有关计算
因为点D是CB的中点,所以CD=CB=6 cm.又因为CE=AC=4 cm.所以ED=EC+CD=4+6=10 cm.
因为点D是CB的中点,所以CD=CB=6 cm.又因为CE=
AC=4 cm.所以ED=EC+CD=4+6=10 cm.
方法归纳交流 计算线段的和差要结合图形寻找已知线段和所求线段的位置、数量关系,因此 观察图形 是关键.
观察图形
角的计数及计算
7.如图,BD平分∠ABC,BE分∠ABC为 2∶5两部分,∠DBE=21°,求∠ABC的度数.
解:设∠ABE=2x°,∠CBE=5x°,则∠ABC=7x°,因为BD平分∠ABC,所以∠ABD=x°,又∠DBE=∠ABD-∠ABE=x°,所以x=21,解得x=14,所以∠ABC=98°.
方法归纳交流 角的计算问题,关键是从图形中寻找和所求角和已知角之间的关系,在解决问题时,注意方程知识在其中的应用.
几何图形初步认识的作业设计
一、作业目标
理解几何图形的概念,熟练线段、角的表示及计算,并能运用所学几何知识解决相关问题.
二、作业内容
1下列语句正确的是 ( D )
A.连接两点的线段叫两点的距离
B.射线AB与射线BA是同一条射线
C.延长线段AB就能得到直线AB
D.延长线段AB到点C,使得BC=AB
D
2如图,这是一个正方体展开图,把展开图折叠成正方体后,“抗”字一面相对面上的字是 ( C )
A.新 B.冠
C.病 D.毒
3若一个棱柱有7个面,则它是 ( C )
A.七棱柱 B.六棱柱
C.五棱柱 D.四棱柱
C
C
4已知∠1=45°24',∠2=45.3°,∠3=45°18',则下列正确的是 ( C )
A.∠1=∠2
B.∠1=∠3
C.∠2=∠3
D.以上都不对
C
5如图,已知∠AOC=∠BOD=80°,∠BOC=25°,则∠AOD的度数为 ( D )
A.150° B.145°
C.140° D.135°
D
6如图,C、D是线段AB上两点,若CB=3 cm,DB=5 cm,且D是AC的中点,则AC的长等于 ( B )
A.2 cm B.4 cm
C.8 cm D.9 cm
B
7如图,电力部门进行“网改”时,都尽量地使电线杆排齐,根据 两点之间线段最短 的数学道理说明这样做可以减少电线的用量.
两点之间线段最短
8 已知∠α与∠β互补,若∠α=43°26',则∠β= 136°34' .
9把一副三角尺按如图所示的方式拼在一起,已知∠BCE=30°.
(1)求∠ACE和∠DCB的度数.
(2)求∠ACD+∠BCE的度数.
136°34'
(3)如果去掉条件“∠BCE=30°”,
那么(2)中的结论还成立吗?为什么?
解:(1)因为∠ACB=∠DCE=90°,∠BCE=30°,
所以∠ACE=60°,∠DCB=60°.
(2)∠ACD+∠BCE=∠ACB+∠DCB+∠BCE=90°+60°+30°=180°.
(3)成立.理由:∠ACD+∠BCE=∠ACB+∠DCB+∠BCE=∠ACB+∠DCE=90°+90°=180°.
10平面上有三个点A,B,C,如果AB=8,AC=5,BC=3,则( A )
A.点C在线段AB上
B.点C在线段AB的延长线上
C.点C在直线AB外
D.不能确定
A
11一个角的余角比它的补角的少20°,则这个角为 ( B )
A.30° B.40°
C.60° D.75°
12在一条直线上有A、B、C三个点,已知AB=12 cm,BC=6 cm,则AB的中点到BC的中点的距离为 ( D )
A.9 cm B.6 cm
C.3 cm D.9 cm或3 cm
B
D
13如图,这是一段火车路线图,A,B,C,D,E是五个火车站,在这条线路上往返行车需要印制 20 种火车票.
20
14如图,这是一个长方体纸盒的平面展开图,已知纸盒中相对的两个面上的数互为相反数.
(1)填空:a= ,b= ,c= .
(2)求代数式的值:a2-|a-b|+|b+c|.
(2)当a=1,b=-2,c=-3时,
a2-|a-b|+|b+c|=1-3+5=3.
解:(1)a=1,b=-2,c=-3.
(2)求AB∶BE的值.
15在同一条直线上从左至右有A、B、C、D四点,且AB∶BC∶CD=4∶5∶7,点E是AD的中点,CD=14.
(1)求线段EC的长;
解:(1)如图,因为AB∶BC∶CD=4∶5∶7,设AB=4x,BC=5x,CD=7x,因为CD=14,所以7x=14,解得x=2.所以AB=8,BC=10,所以AC=AB+BC=18,AD=AC+CD=18+14=32,因为E是AD的中点,所以AE=AD=16,EC=AC-AE=18-16=2;
(2)BE=AE-AB=16-8=8,AB=8,所以AB∶BE=1∶1=1.
16如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
解:(1)因为∠AOB是直角,∠AOC=40°, 所以∠AOB+∠AOC=90°+40°=130°,
因为OM是∠BOC的平分线,ON是∠AOC的平分线,
所以∠MOC=∠BOC=65°,∠NOC=∠AOC=20°.
所以∠MON=∠MOC-∠NOC=65°-20°=45°,
(2)当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
因为∠MON=∠MOC-∠NOC=∠BOC-∠AOC=(∠BOC-∠AOC)=∠AOB,
又∠AOB是直角,不改变, 所以∠MON=∠AOB=45°.
17如图,C是线段AB上一点,AB=20 cm,BC=8 cm,点P从A出发,以2 cm/s的速度沿AB向右运动,终点为B;点Q从点B出发,以1 cm/s的速度沿BA向左运动,终点为A.已知P、Q同时出发,当其中一点到达终点时,另一点也随之停止运功.设点P运动时间为x s.
(1)AC= cm.
(2)当x= s时,P,Q重合.
(3)是否存在某一时刻,使得C,P,Q这三个点中,有一个点恰为另外两点所连线段的中点?若存在,求出所有满足条件的x的值;若不存在,请说明理由.
解:(1)AC=AB-BC=20-8=12(cm).故答案为12.
(2)20÷(2+1)=.故当x=时,P,Q重合.
(3)存在,①当C是线段PQ的中点时,得2x+20-x=2×12,解得x=4;
②当P为线段CQ的中点,得12+20-x=2×2x,解得x=;
③当Q为线段PC的中点,得2x+12=2×(20-x),解得x=7.
综上所述,x=4或x=或x=7.
第四章 图形的认识
第四章 复习课
1.知道几何图形包括平面图形与立体图形,能说出常见的立体图形和平面图形的名称.
2.知道线段、射线、直线和角的表示方法,会进行的度、分、秒的换算;会作一条线段等于已知线段.
3.知道线段中点及角平分线的含义,会进行相关的计算.
4.熟记两个基本事实,并能应用它们解决实际问题.
◎重点:线段中点、角平分线的概念,线段和角的有关计算.
◎难点:熟练地进行线段和角的计算.
在这一章中,我们学习了哪些知识?你能用知识框图表示本章所学内容吗?
立体
平面
两点
度量
线段
度量
叠合
相等
相等
叠合
1.点与直线的位置关系有: 点在直线上(直线经过点) 、 点在直线外(直线不经过点) .
2.如图,若点B是线段AC的中点,则 AB = BC = AC .
点在直线上(直线经过点)
点在直线外(直线不经过点)
AB
BC
AC
3.如图,若OC是∠AOB的平分线,则∠AOC= ∠BOC = ∠AOB.
∠BOC
4.1°= 60 '= 3600 ″;1'= 60 ″;
1'=°;1″='.
5.若∠A与∠B互余,则∠A+∠B= 90° ;若∠A与∠C互补,则∠A+∠C= 180° .
60
3600
60
90°
180°
立体图形与平面图形
1.在圆、正方形、圆锥、长方体、线段、球、三棱柱、直角三角形中,是立体图形的有 圆锥、长方体、球、三棱柱 ,是平面图形的有 圆、正方形、线段、直角三角形 .
圆锥、长方体、球、三棱柱
圆、正方形、线段、直角三角形
2.下列说法:①射线AB与射线BA表示的是同一条射线;②线段AB与线段BA表示的不是同一条线段;③直线AB与直线BA表示的是同一条直线;④线段、射线都是直线的一部分.其中,正确的是 ③④ .(填序号)
③④
直线、射线、线段
3.“把弯曲的公路改直,就能缩短路程”,其中蕴含的数学道理是 ( D )
A.两点确定一条直线
B.直线比曲线短
C.两点之间直线最短
D.两点之间线段最短
4.如图,可以用字母表示出来的不同线段有 10 条.
D
10
变式训练 (1)往返于A,B两个城市的客车,中途有三个停靠点,该客车有 10 种不同的票价,该客车上要准备 20 种车票.
(2)有5个人,每两个人握一次手一共要握 10 次手.
10
20
10
方法归纳交流 线段的总条数N与线段上的已知点数n的关系是 N= .
N=
数几何图形的个数
如图,回答下列问题:
(1)图中有几条直线?能用字母表示出来的有哪些?
(2)图中有几条射线?用字母表示出来.
(3)图中有几条线段?用字母表示出来.
解:(1)图中有1条直线,表示为直线AD(或直线AB、AC、BD、BC、CD).
(2)共有8条射线,能用字母表示的有射线AB、BA、BC、CB、CD、DC.
(3)共有6条线段,表示为线段AB、AC、AD、BC、BD、CD.
5.如图,有四个点A、B、C、D,按照下列语句画出图形:
(1)画直线AB;
(2)画射线BD;
(3)作线段BC,并以厘米为单位,度量其长度;
(4)线段AC和线段BD相交于点O;
(5)反向延长线段BC至点E,使BE=BC.
解:如图.BC=0.6 cm.
6.已知线段AB=24 cm,点C是线段AB的中点,点D是CB的中点,点E在线段AC上,且CE=AC.画图并计算ED的长.
解:如图,因为点C是AB的中点,AB=24 cm,所以AC=CB=AB=12 cm.
线段的有关计算
因为点D是CB的中点,所以CD=CB=6 cm.又因为CE=AC=4 cm.所以ED=EC+CD=4+6=10 cm.
因为点D是CB的中点,所以CD=CB=6 cm.又因为CE=
AC=4 cm.所以ED=EC+CD=4+6=10 cm.
方法归纳交流 计算线段的和差要结合图形寻找已知线段和所求线段的位置、数量关系,因此 观察图形 是关键.
观察图形
角的计数及计算
7.如图,BD平分∠ABC,BE分∠ABC为 2∶5两部分,∠DBE=21°,求∠ABC的度数.
解:设∠ABE=2x°,∠CBE=5x°,则∠ABC=7x°,因为BD平分∠ABC,所以∠ABD=x°,又∠DBE=∠ABD-∠ABE=x°,所以x=21,解得x=14,所以∠ABC=98°.
方法归纳交流 角的计算问题,关键是从图形中寻找和所求角和已知角之间的关系,在解决问题时,注意方程知识在其中的应用.
几何图形初步认识的作业设计
一、作业目标
理解几何图形的概念,熟练线段、角的表示及计算,并能运用所学几何知识解决相关问题.
二、作业内容
1下列语句正确的是 ( D )
A.连接两点的线段叫两点的距离
B.射线AB与射线BA是同一条射线
C.延长线段AB就能得到直线AB
D.延长线段AB到点C,使得BC=AB
D
2如图,这是一个正方体展开图,把展开图折叠成正方体后,“抗”字一面相对面上的字是 ( C )
A.新 B.冠
C.病 D.毒
3若一个棱柱有7个面,则它是 ( C )
A.七棱柱 B.六棱柱
C.五棱柱 D.四棱柱
C
C
4已知∠1=45°24',∠2=45.3°,∠3=45°18',则下列正确的是 ( C )
A.∠1=∠2
B.∠1=∠3
C.∠2=∠3
D.以上都不对
C
5如图,已知∠AOC=∠BOD=80°,∠BOC=25°,则∠AOD的度数为 ( D )
A.150° B.145°
C.140° D.135°
D
6如图,C、D是线段AB上两点,若CB=3 cm,DB=5 cm,且D是AC的中点,则AC的长等于 ( B )
A.2 cm B.4 cm
C.8 cm D.9 cm
B
7如图,电力部门进行“网改”时,都尽量地使电线杆排齐,根据 两点之间线段最短 的数学道理说明这样做可以减少电线的用量.
两点之间线段最短
8 已知∠α与∠β互补,若∠α=43°26',则∠β= 136°34' .
9把一副三角尺按如图所示的方式拼在一起,已知∠BCE=30°.
(1)求∠ACE和∠DCB的度数.
(2)求∠ACD+∠BCE的度数.
136°34'
(3)如果去掉条件“∠BCE=30°”,
那么(2)中的结论还成立吗?为什么?
解:(1)因为∠ACB=∠DCE=90°,∠BCE=30°,
所以∠ACE=60°,∠DCB=60°.
(2)∠ACD+∠BCE=∠ACB+∠DCB+∠BCE=90°+60°+30°=180°.
(3)成立.理由:∠ACD+∠BCE=∠ACB+∠DCB+∠BCE=∠ACB+∠DCE=90°+90°=180°.
10平面上有三个点A,B,C,如果AB=8,AC=5,BC=3,则( A )
A.点C在线段AB上
B.点C在线段AB的延长线上
C.点C在直线AB外
D.不能确定
A
11一个角的余角比它的补角的少20°,则这个角为 ( B )
A.30° B.40°
C.60° D.75°
12在一条直线上有A、B、C三个点,已知AB=12 cm,BC=6 cm,则AB的中点到BC的中点的距离为 ( D )
A.9 cm B.6 cm
C.3 cm D.9 cm或3 cm
B
D
13如图,这是一段火车路线图,A,B,C,D,E是五个火车站,在这条线路上往返行车需要印制 20 种火车票.
20
14如图,这是一个长方体纸盒的平面展开图,已知纸盒中相对的两个面上的数互为相反数.
(1)填空:a= ,b= ,c= .
(2)求代数式的值:a2-|a-b|+|b+c|.
(2)当a=1,b=-2,c=-3时,
a2-|a-b|+|b+c|=1-3+5=3.
解:(1)a=1,b=-2,c=-3.
(2)求AB∶BE的值.
15在同一条直线上从左至右有A、B、C、D四点,且AB∶BC∶CD=4∶5∶7,点E是AD的中点,CD=14.
(1)求线段EC的长;
解:(1)如图,因为AB∶BC∶CD=4∶5∶7,设AB=4x,BC=5x,CD=7x,因为CD=14,所以7x=14,解得x=2.所以AB=8,BC=10,所以AC=AB+BC=18,AD=AC+CD=18+14=32,因为E是AD的中点,所以AE=AD=16,EC=AC-AE=18-16=2;
(2)BE=AE-AB=16-8=8,AB=8,所以AB∶BE=1∶1=1.
16如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
解:(1)因为∠AOB是直角,∠AOC=40°, 所以∠AOB+∠AOC=90°+40°=130°,
因为OM是∠BOC的平分线,ON是∠AOC的平分线,
所以∠MOC=∠BOC=65°,∠NOC=∠AOC=20°.
所以∠MON=∠MOC-∠NOC=65°-20°=45°,
(2)当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
因为∠MON=∠MOC-∠NOC=∠BOC-∠AOC=(∠BOC-∠AOC)=∠AOB,
又∠AOB是直角,不改变, 所以∠MON=∠AOB=45°.
17如图,C是线段AB上一点,AB=20 cm,BC=8 cm,点P从A出发,以2 cm/s的速度沿AB向右运动,终点为B;点Q从点B出发,以1 cm/s的速度沿BA向左运动,终点为A.已知P、Q同时出发,当其中一点到达终点时,另一点也随之停止运功.设点P运动时间为x s.
(1)AC= cm.
(2)当x= s时,P,Q重合.
(3)是否存在某一时刻,使得C,P,Q这三个点中,有一个点恰为另外两点所连线段的中点?若存在,求出所有满足条件的x的值;若不存在,请说明理由.
解:(1)AC=AB-BC=20-8=12(cm).故答案为12.
(2)20÷(2+1)=.故当x=时,P,Q重合.
(3)存在,①当C是线段PQ的中点时,得2x+20-x=2×12,解得x=4;
②当P为线段CQ的中点,得12+20-x=2×2x,解得x=;
③当Q为线段PC的中点,得2x+12=2×(20-x),解得x=7.
综上所述,x=4或x=或x=7.
同课章节目录
