2022-2023学年湘教版七年级数学上册4.3.2第2课时互余与互补 课件(共31张PPT)
文档属性
| 名称 | 2022-2023学年湘教版七年级数学上册4.3.2第2课时互余与互补 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 583.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-01 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
第四章 图形的认识
4.3.2 角的度量与计算
第2课时 互余与互补
1.知道两角互余、两角互补的意义,能熟练地求一个角的余角或补角.
2.通过探究,知道“同角(或等角)的余角相等”,“同角(或等角)的补角相等”,并会应用.
◎重点:余角、补角的概念及性质.
◎难点:余角、补角的性质.
大家知道比萨斜塔吗?比萨斜塔因为倾斜而出名,现在已知塔身倾斜了约5.5°,那么你知道塔身和地面成多少度角吗?
余角和补角的定义
阅读课本“做一做”至“动脑筋”的内容,填空:
1.如果两个角的和等于一个 直角 ,那么说这两个角互为余角,(简称 互余 ),也说其中一个角是另一个角的 余角 .
2.如果两个角的和等于一个 平角 ,那么说这两个角互为补角,(简称 互补 ),也说其中一个角是另一个角的 补角 .
直角
互余
余
角
平角
互补
补
角
已知∠1=55°,则∠1的余角等于 35° ,∠1的补角等于 125° .
35°
125°
余角、补角的性质
1.阅读课本“动脑筋”的内容,并在下面完成解答过程.
(1)答: ∠2与∠3相等 .理由: 因为∠1+∠2=180°,∠1+∠3=180°,所以∠2=180°-∠1,∠3=180°-∠1,所以∠2=∠3 .
(2)答: ∠5与∠6相等 .理由: 因为∠4+∠5=90°,∠4+∠6=90°,所以∠5=90°-∠4,∠6=90°-∠4,所以∠5=∠6 .
∠2与∠3相等
因为∠1+∠2=180°,
∠1+∠3=180°,所以∠2=180°-∠1,∠3=180°-∠1,
所以∠2=∠3
∠5与∠6相等
因为∠4+∠5=90°,
∠4+∠6=90°,所以∠5=90°-∠4,∠6=90°-∠4,所
以∠5=∠6
2.如果∠1与∠2互补,∠4与∠3互补,且∠1=∠4,那么∠3与∠2有什么关系?为什么?
解:∠3=∠2.理由:因为∠1+∠2=180°,∠4+∠3=180°,所以∠2=180°-∠1,∠3=180°-∠4.
又∠1=∠4,所以∠2=∠3.
3.如果∠1与∠2互余,∠4与∠3互余,且∠1=∠4,那么∠3与∠2的大小关系是 相等 .
归纳总结 同角(或等角)的补角 相等 .
同角(或等角)的余角 相等 .
相等
相等
相等
根据余角和补角的定义求角的度数
1.25°的余角和补角分别是多少度?一个角的补角比它的余角大多少度?
解:65°,155°.设这个角为x°,则它的补角为(180-x)°,它的余角为(90-x)°,(180-x)-(90-x)=90,即这个角的补角比它的余角大90°.
变式训练 一个角的余角比它的补角的还多1°,求这个角的度数.
解:设这个角为x°,则90-x=(180-x)+1,解得x=63.
答:这个角的度数为63°.
2.已知∠1与∠2互余,∠2与∠3互补,∠1=65°,则∠3= ( D )
A.65° B.25° C.115° D.155°
D
方法归纳交流 求一个角的余角,就是用 90 °减去这个角的度数;求一个角的补角,就是用 180 °减去这个角的度数.
90
180
利用余角、补角的性质进行简单推理
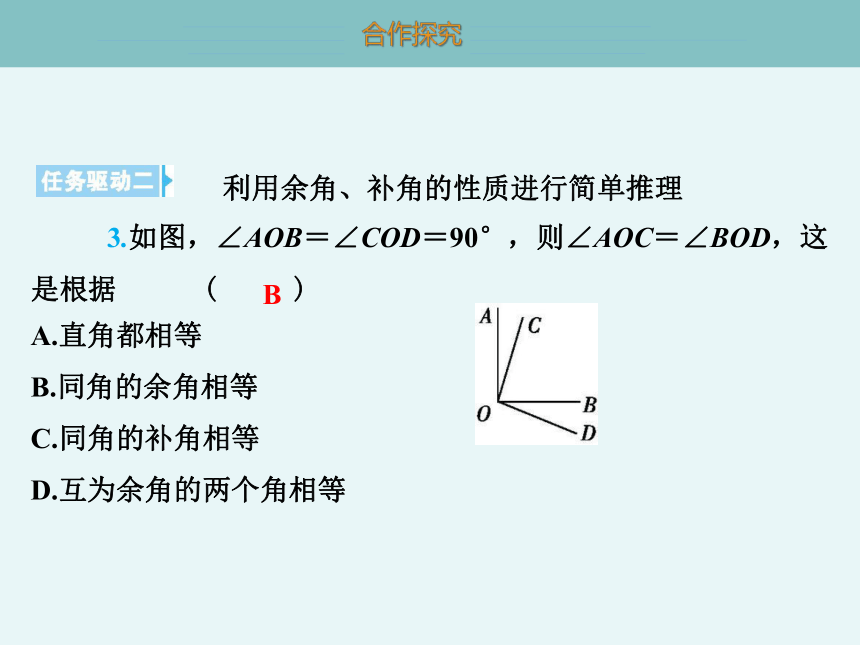
3.如图,∠AOB=∠COD=90°,则∠AOC=∠BOD,这是根据 ( B )
A.直角都相等
B.同角的余角相等
C.同角的补角相等
D.互为余角的两个角相等
B
判定一个角的余角、补角
4.如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,射线OE在∠BOC内,∠BOE=∠EOC,∠EOC=90°.
(1)求∠DOE的度数;
(2)哪些角与∠AOD互为余角?
(3)互为补角的角有几对?请分别写出来.
解:(1)因为∠BOE=∠EOC,∠EOC=90°,所以∠BOE=×90°=30°,所以∠AOB=180°-∠EOC-∠BOE=180°-90°-30°=60°.因为OD平分∠AOB,所以∠BOD=∠AOB=30°,所以∠DOE=∠BOD+∠BOE=60°.
(2)因为∠AOD=30°,∠AOB=60°,∠DOE=60°,所以∠AOB,∠DOE与∠AOD互为余角.
(3)6对.∠AOD与∠DOC,∠AOB与∠BOC,∠AOE与∠EOC,∠BOD与∠DOC,∠BOE与∠DOC,∠EOD与∠BOC.
角平分线与角的余角、补角的综合运用
如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=64°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和
∠AOE的余角.
解:(1)因为∠AOC=64°,所以∠AOD=180°-∠AOC=180°-64°=116°,
因为OE平分∠AOD,所以∠DOE=∠AOD=×116°=58°,
因为∠AOC+∠AOD=∠BOD+∠AOD=180°,所以∠BOD=∠AOC=64°,
因为OF平分∠BOD,所以∠DOF=∠BOD=×64°=32°,
所以∠EOF=∠DOE+∠DOF=58°+32°=90°;
(2)∠AOD的补角有∠AOC和∠BOD;∠AOE的余角有∠BOF和∠DOF.
因为OF平分∠BOD,所以∠DOF=∠BOD=×64°=
32°,
所以∠EOF=∠DOE+∠DOF=58°+32°=90°;
1已知∠A=70°,则∠A的余角等于( A )
A.20° B.30° C.70° D.110°
2如图,点O在直线AB上,若∠1=40°,则∠2的度数是( C )
A.50° B.60°
C.140° D.150°
A
C
3一个角的余角是这个角补角的三分之一,则这个角是( B )
A.30° B.45°
C.60° D.90°
B
4如图,已知∠AOB是直角,C、O、D三点在同一条直线上,∠AOC=25°,则∠AOC的余角的补角为 115° .
115°
5若一个角的补角比它的余角的2倍还多70°,则这个角的度数是多少?
解:设这个角的度数是x°,则它的补角为(180-x)°,余角为(90-x)°,
由题意,得(180-x)-2(90-x)=70.解得x=70.
答:这个角的度数为70°
6下列说法正确的是 ( A )
A.一个锐角的余角比这个角的补角小90°
B.如果一个角有补角,那么这个角必是钝角
C.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互为补角
D.如果∠α和∠β互为余角,∠β与∠θ互为余角,那么∠α与∠θ互为余角
A
7在同一平面内,∠AOB=70°,∠AOC是∠AOB的余角,OD平分∠BOC,则∠DOC= 45°或25° .
8如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是 ∠BOC .
45°或25°
∠BOC
9若β是α的补角,γ是α的余角,且β与γ的和是平角,则β是α的 11 倍.
11
10如图,点O在直线AB上,作射线OC,点D在平面内,∠BOD与∠AOC互余.
(1)若∠AOC∶∠BOD=4∶5,则∠BOD= ;
(2)若∠AOC=α(0°<α≤45°),ON平分∠COD,补全图形,求出∠AON的值(用含α的式子表示).
解:(1)∵∠AOC∶∠BOD=4∶5,∠BOD与∠AOC互余,
∴∠BOD=90°×=50°.
(2)∵∠BOD与∠AOC互余,∴∠BOD+∠AOC=90°.
情形一:点D在∠BOC内.在0°<α≤45°的条件下,补全图形如下:
∴∠COD=90°,∵ON平分∠COD,∴∠CON=45°,
∴∠COD=90°.∵ON平分∠COD,∴∠CON=45°,
∴∠AON=α+45°.
情形二:点D在∠BOC外.在0°<α≤45°的条件下,补全图形如下:
∴∠AON=α+45°.
∠COD=90°+2α,∠CON=45°+α,
此时∠AON=45°.
∠COD=90°+2α,∠CON=45°+α,
此时∠AON=45°.
第四章 图形的认识
4.3.2 角的度量与计算
第2课时 互余与互补
1.知道两角互余、两角互补的意义,能熟练地求一个角的余角或补角.
2.通过探究,知道“同角(或等角)的余角相等”,“同角(或等角)的补角相等”,并会应用.
◎重点:余角、补角的概念及性质.
◎难点:余角、补角的性质.
大家知道比萨斜塔吗?比萨斜塔因为倾斜而出名,现在已知塔身倾斜了约5.5°,那么你知道塔身和地面成多少度角吗?
余角和补角的定义
阅读课本“做一做”至“动脑筋”的内容,填空:
1.如果两个角的和等于一个 直角 ,那么说这两个角互为余角,(简称 互余 ),也说其中一个角是另一个角的 余角 .
2.如果两个角的和等于一个 平角 ,那么说这两个角互为补角,(简称 互补 ),也说其中一个角是另一个角的 补角 .
直角
互余
余
角
平角
互补
补
角
已知∠1=55°,则∠1的余角等于 35° ,∠1的补角等于 125° .
35°
125°
余角、补角的性质
1.阅读课本“动脑筋”的内容,并在下面完成解答过程.
(1)答: ∠2与∠3相等 .理由: 因为∠1+∠2=180°,∠1+∠3=180°,所以∠2=180°-∠1,∠3=180°-∠1,所以∠2=∠3 .
(2)答: ∠5与∠6相等 .理由: 因为∠4+∠5=90°,∠4+∠6=90°,所以∠5=90°-∠4,∠6=90°-∠4,所以∠5=∠6 .
∠2与∠3相等
因为∠1+∠2=180°,
∠1+∠3=180°,所以∠2=180°-∠1,∠3=180°-∠1,
所以∠2=∠3
∠5与∠6相等
因为∠4+∠5=90°,
∠4+∠6=90°,所以∠5=90°-∠4,∠6=90°-∠4,所
以∠5=∠6
2.如果∠1与∠2互补,∠4与∠3互补,且∠1=∠4,那么∠3与∠2有什么关系?为什么?
解:∠3=∠2.理由:因为∠1+∠2=180°,∠4+∠3=180°,所以∠2=180°-∠1,∠3=180°-∠4.
又∠1=∠4,所以∠2=∠3.
3.如果∠1与∠2互余,∠4与∠3互余,且∠1=∠4,那么∠3与∠2的大小关系是 相等 .
归纳总结 同角(或等角)的补角 相等 .
同角(或等角)的余角 相等 .
相等
相等
相等
根据余角和补角的定义求角的度数
1.25°的余角和补角分别是多少度?一个角的补角比它的余角大多少度?
解:65°,155°.设这个角为x°,则它的补角为(180-x)°,它的余角为(90-x)°,(180-x)-(90-x)=90,即这个角的补角比它的余角大90°.
变式训练 一个角的余角比它的补角的还多1°,求这个角的度数.
解:设这个角为x°,则90-x=(180-x)+1,解得x=63.
答:这个角的度数为63°.
2.已知∠1与∠2互余,∠2与∠3互补,∠1=65°,则∠3= ( D )
A.65° B.25° C.115° D.155°
D
方法归纳交流 求一个角的余角,就是用 90 °减去这个角的度数;求一个角的补角,就是用 180 °减去这个角的度数.
90
180
利用余角、补角的性质进行简单推理
3.如图,∠AOB=∠COD=90°,则∠AOC=∠BOD,这是根据 ( B )
A.直角都相等
B.同角的余角相等
C.同角的补角相等
D.互为余角的两个角相等
B
判定一个角的余角、补角
4.如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,射线OE在∠BOC内,∠BOE=∠EOC,∠EOC=90°.
(1)求∠DOE的度数;
(2)哪些角与∠AOD互为余角?
(3)互为补角的角有几对?请分别写出来.
解:(1)因为∠BOE=∠EOC,∠EOC=90°,所以∠BOE=×90°=30°,所以∠AOB=180°-∠EOC-∠BOE=180°-90°-30°=60°.因为OD平分∠AOB,所以∠BOD=∠AOB=30°,所以∠DOE=∠BOD+∠BOE=60°.
(2)因为∠AOD=30°,∠AOB=60°,∠DOE=60°,所以∠AOB,∠DOE与∠AOD互为余角.
(3)6对.∠AOD与∠DOC,∠AOB与∠BOC,∠AOE与∠EOC,∠BOD与∠DOC,∠BOE与∠DOC,∠EOD与∠BOC.
角平分线与角的余角、补角的综合运用
如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=64°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和
∠AOE的余角.
解:(1)因为∠AOC=64°,所以∠AOD=180°-∠AOC=180°-64°=116°,
因为OE平分∠AOD,所以∠DOE=∠AOD=×116°=58°,
因为∠AOC+∠AOD=∠BOD+∠AOD=180°,所以∠BOD=∠AOC=64°,
因为OF平分∠BOD,所以∠DOF=∠BOD=×64°=32°,
所以∠EOF=∠DOE+∠DOF=58°+32°=90°;
(2)∠AOD的补角有∠AOC和∠BOD;∠AOE的余角有∠BOF和∠DOF.
因为OF平分∠BOD,所以∠DOF=∠BOD=×64°=
32°,
所以∠EOF=∠DOE+∠DOF=58°+32°=90°;
1已知∠A=70°,则∠A的余角等于( A )
A.20° B.30° C.70° D.110°
2如图,点O在直线AB上,若∠1=40°,则∠2的度数是( C )
A.50° B.60°
C.140° D.150°
A
C
3一个角的余角是这个角补角的三分之一,则这个角是( B )
A.30° B.45°
C.60° D.90°
B
4如图,已知∠AOB是直角,C、O、D三点在同一条直线上,∠AOC=25°,则∠AOC的余角的补角为 115° .
115°
5若一个角的补角比它的余角的2倍还多70°,则这个角的度数是多少?
解:设这个角的度数是x°,则它的补角为(180-x)°,余角为(90-x)°,
由题意,得(180-x)-2(90-x)=70.解得x=70.
答:这个角的度数为70°
6下列说法正确的是 ( A )
A.一个锐角的余角比这个角的补角小90°
B.如果一个角有补角,那么这个角必是钝角
C.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互为补角
D.如果∠α和∠β互为余角,∠β与∠θ互为余角,那么∠α与∠θ互为余角
A
7在同一平面内,∠AOB=70°,∠AOC是∠AOB的余角,OD平分∠BOC,则∠DOC= 45°或25° .
8如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是 ∠BOC .
45°或25°
∠BOC
9若β是α的补角,γ是α的余角,且β与γ的和是平角,则β是α的 11 倍.
11
10如图,点O在直线AB上,作射线OC,点D在平面内,∠BOD与∠AOC互余.
(1)若∠AOC∶∠BOD=4∶5,则∠BOD= ;
(2)若∠AOC=α(0°<α≤45°),ON平分∠COD,补全图形,求出∠AON的值(用含α的式子表示).
解:(1)∵∠AOC∶∠BOD=4∶5,∠BOD与∠AOC互余,
∴∠BOD=90°×=50°.
(2)∵∠BOD与∠AOC互余,∴∠BOD+∠AOC=90°.
情形一:点D在∠BOC内.在0°<α≤45°的条件下,补全图形如下:
∴∠COD=90°,∵ON平分∠COD,∴∠CON=45°,
∴∠COD=90°.∵ON平分∠COD,∴∠CON=45°,
∴∠AON=α+45°.
情形二:点D在∠BOC外.在0°<α≤45°的条件下,补全图形如下:
∴∠AON=α+45°.
∠COD=90°+2α,∠CON=45°+α,
此时∠AON=45°.
∠COD=90°+2α,∠CON=45°+α,
此时∠AON=45°.
同课章节目录
