2022-2023学年湘教版七年级数学上册4.3.2第1课时角的度量与计算 课件(共27张PPT)
文档属性
| 名称 | 2022-2023学年湘教版七年级数学上册4.3.2第1课时角的度量与计算 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 567.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-01 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第四章 图形的认识
4.3.2 角的度量与计算
第1课时 角的度量与计算
1.知道直角、锐角、钝角的概念及直角、平角、周角之间的关系.
2.知道角的度量单位及换算,并能进行角的加减运算.
◎重点:角的度量的换算,角的加减运算.
◎难点:度、分、秒之间的互化.
我们要比较两个角哪个大,大多少,需要测量.为了准确测量出角的大小,要有统一的计量单位和度量工具.这一节课,我们就一起来学习角的度量与计算.
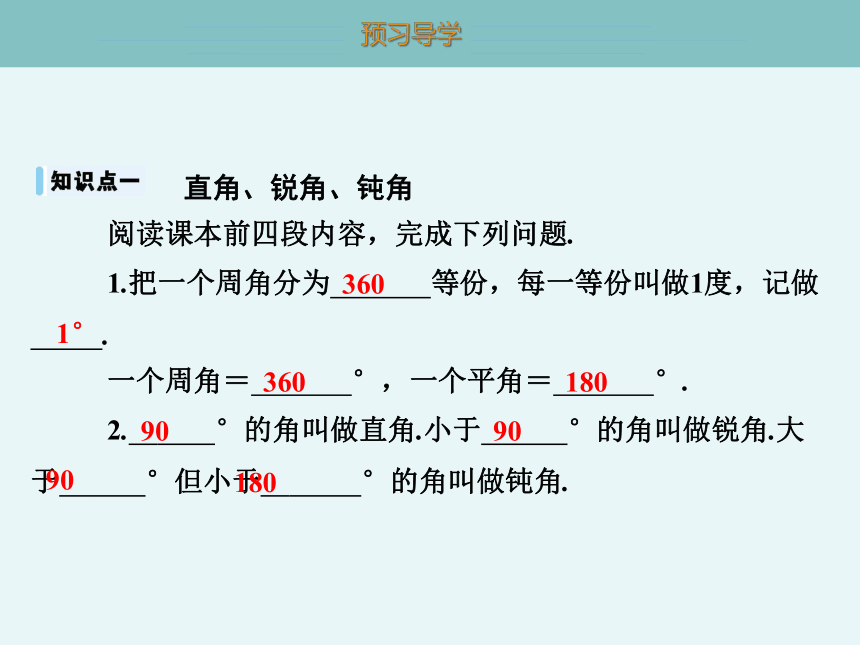
直角、锐角、钝角
阅读课本前四段内容,完成下列问题.
1.把一个周角分为 360 等份,每一等份叫做1度,记做 1° .
一个周角= 360 °,一个平角= 180 °.
2. 90 °的角叫做直角.小于 90 °的角叫做锐角.大于 90 °但小于 180 °的角叫做钝角.
360
1°
360
180
90
90
90
180
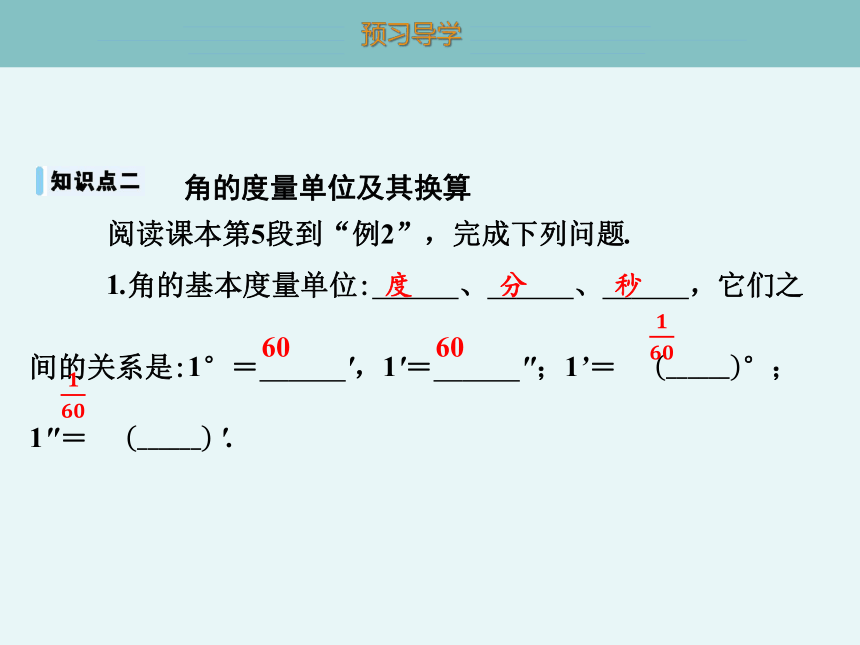
角的度量单位及其换算
阅读课本第5段到“例2”,完成下列问题.
1.角的基本度量单位: 度 、 分 、 秒 ,它们之间的关系是:1°= 60 ',1'= 60 ″;1’= °;1″= '.
度
分
秒
60
60
2.如何把57.32°转化成用度、分、秒表示?
答:先把0.32°化为分,0.32°=60'×0.32=19.2',再把0.2'化成秒,0.2'=60″×0.2=12″.所以57.32°=57°19'12″.
3.如何把10°6'36″用度表示?
解:先把36″化成分,36″='×36=0.6', 6'+0.6'=6.6',再把6.6'化成度,6.6'=°×6.6=0.11°.
所以10°6'36″=10.11°.
归纳总结 把度化成分或把分化成秒的过程乘以 60 ;把分化成度或把秒化成分的过程乘以 .
解:先把36″化成分,36″='×36=0.6', 6'+0.6'=6.6',
再把6.6'化成度,6.6'=°×6.6=0.11°.
所以10°6'36″=10.11°.
60
角的加减计算
阅读课本“例3”回答问题:
1.进行角的加法运算,把度与 度 、分与 分 、秒与 秒 单位上的数分别相加,然后把满60″的进为 1' ,再把满60'的进为 1° .
2.进行角的减法运算,把度与 度 、分与 分 、秒与 秒 单位上的数分别相减,当被减数的分(秒)不足时,要借1°(1')当 60' ( 60″ ).
度
分
秒
1'
1°
度
分
秒
60'
60″
角度的单位换算
1.用度、分、秒表示26.24°.
解:先把0.24°化成分,0.24°=60'×0.24=14.4'.0.4'=60″×0.4=24″.所以26.24°=26°14'24″.
2.将36°45'18″化为用度表示.
解:先把18″化成分,18″='×18=0.3',45'+0.3'=45.3'.45.3'=°×45.3=0.755°.
所以36°45'18″=36.755°.
变式训练 若∠1=36°18',∠2=36.3°,∠3=36.18°,则 ( A )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.以上都不对
A
方法归纳交流 (1)把角的度数用“度、分、秒”表示时,先把不够1度的角化为 分 ,再把不够 1分 的角化为 秒 ;把角的度数由“度、分、秒”化为“度”时,先把 秒 转化为 分 ,再把 分 化为 度 .
(2)比较几个角的大小时,如果单位不统一,应先 统一单位 ,再比较大小.
分
1分
秒
秒
分
分
度
统一单
位
角的和与差的计算
3.在同一平面上,若∠AOB=50°, ∠BOC=15°,求∠AOC的度数.
解:如图1,当OC在∠AOB外部时,∠AOC=∠AOB+∠BOC=50°+15°=65°,
如图2,当OC在∠AOB内部时,∠AOC=∠AOB-∠BOC=50°-15°=35°,
所以∠AOC的度数是65°或35°.
4.计算:(1)46°39'40″+63°41'35″;
(2)86°23'12″-67°36'50″;
(3)180°-79°19'15″.
解:(1)110°21'15″;
(2)18°46'22″;
(3)100°40'45″.
钟表中的角
7点半时,钟面上时针和分针的夹角是 45° .
45°
1下列4个角中,属于锐角的是 ( A )
A.50° B.90° C.110° D.130°
2如图,下列式子中错误的是 ( C )
A.∠AOC=∠AOB+∠BOC
B.∠AOC=∠AOD-∠COD
C.∠AOC=∠AOB+∠BOD-∠BOC
D.∠AOC=∠AOD-∠BOD+∠BOC
A
C
3按要求解题:
(1)用度、分、秒表示:①48.26°;②37.37°;
(2)用度表示:①37°24'36″;②13°37'48″.
解:(1)①48.26°=48°15'36″;②37.37°=37°22'12″;
(2)①37°24'36″=37.41°;②13°37'48″=13.63°.
4计算:(1)48°29'+67°41';(2)180°-74°13'26″.
解:(1)原式=116°10';
(2)原式=105°46'34″.
5若∠A=20°18',∠B=20°15'30″,∠C=20.25°,则( A )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
A
6如图,已知点M是直线AB上一点,∠AMC=52°48',∠BMD=72°19',则∠CMD等于 ( B )
A.49°07' B.54°53'
C.55°53' D.53°7'
B
7下列算式:①33.33°=33°3'3″;②33.33°=33°19'48″;③50°40'30″=50.43°;④50°40'30″=50.675°,其中正确的是( D )
A.①和② B.①和③
C.②和③ D.②和④
D
8如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 180 度.
180
9如图,OB平分∠AOC,∠AOD=76°.
(1)若∠BOC=20°,求∠COD的度数;
(2)若OC是∠AOD的平分线,求∠BOD的度数.
解:(1)因为OB平分∠AOC,所以∠AOC=2∠BOC=40°,所以∠COD=∠AOD-∠AOC=76°-40°=36°.
(2)因为OC是∠AOD的平分线,所以∠AOC=∠AOD=38°,因为OB平分∠AOC,所以∠AOB=∠AOC=19°,所以∠BOD=∠AOD-∠AOB=76°-19°=57°.
10(1)从1点15分到1点35分,时钟的分针与时针各转过了多大角度?
(2)1点20分时,时钟的时针与分针的夹角是几度?2点15分时,时钟的时针与分针的夹角又是几度?
解:(1)从1点15分到1点35分,分针共走了20小格.所以分针转过的角度是(35-15)×=120°,
时针转过的角度是×120°=10°.
(2)因为分针每分钟走1小格,时针每分钟走小格,
所以1点20分时,时针与分针的夹角是 20- 5+×20 ×=80°.
2点15分时,时针与分针的夹角是 15- 10+×15 ×=22.5°.
所以1点20分时,时针与分针的夹角是
×=80°.
2点15分时,时针与分针的夹角是
×=22.5°.
第四章 图形的认识
4.3.2 角的度量与计算
第1课时 角的度量与计算
1.知道直角、锐角、钝角的概念及直角、平角、周角之间的关系.
2.知道角的度量单位及换算,并能进行角的加减运算.
◎重点:角的度量的换算,角的加减运算.
◎难点:度、分、秒之间的互化.
我们要比较两个角哪个大,大多少,需要测量.为了准确测量出角的大小,要有统一的计量单位和度量工具.这一节课,我们就一起来学习角的度量与计算.
直角、锐角、钝角
阅读课本前四段内容,完成下列问题.
1.把一个周角分为 360 等份,每一等份叫做1度,记做 1° .
一个周角= 360 °,一个平角= 180 °.
2. 90 °的角叫做直角.小于 90 °的角叫做锐角.大于 90 °但小于 180 °的角叫做钝角.
360
1°
360
180
90
90
90
180
角的度量单位及其换算
阅读课本第5段到“例2”,完成下列问题.
1.角的基本度量单位: 度 、 分 、 秒 ,它们之间的关系是:1°= 60 ',1'= 60 ″;1’= °;1″= '.
度
分
秒
60
60
2.如何把57.32°转化成用度、分、秒表示?
答:先把0.32°化为分,0.32°=60'×0.32=19.2',再把0.2'化成秒,0.2'=60″×0.2=12″.所以57.32°=57°19'12″.
3.如何把10°6'36″用度表示?
解:先把36″化成分,36″='×36=0.6', 6'+0.6'=6.6',再把6.6'化成度,6.6'=°×6.6=0.11°.
所以10°6'36″=10.11°.
归纳总结 把度化成分或把分化成秒的过程乘以 60 ;把分化成度或把秒化成分的过程乘以 .
解:先把36″化成分,36″='×36=0.6', 6'+0.6'=6.6',
再把6.6'化成度,6.6'=°×6.6=0.11°.
所以10°6'36″=10.11°.
60
角的加减计算
阅读课本“例3”回答问题:
1.进行角的加法运算,把度与 度 、分与 分 、秒与 秒 单位上的数分别相加,然后把满60″的进为 1' ,再把满60'的进为 1° .
2.进行角的减法运算,把度与 度 、分与 分 、秒与 秒 单位上的数分别相减,当被减数的分(秒)不足时,要借1°(1')当 60' ( 60″ ).
度
分
秒
1'
1°
度
分
秒
60'
60″
角度的单位换算
1.用度、分、秒表示26.24°.
解:先把0.24°化成分,0.24°=60'×0.24=14.4'.0.4'=60″×0.4=24″.所以26.24°=26°14'24″.
2.将36°45'18″化为用度表示.
解:先把18″化成分,18″='×18=0.3',45'+0.3'=45.3'.45.3'=°×45.3=0.755°.
所以36°45'18″=36.755°.
变式训练 若∠1=36°18',∠2=36.3°,∠3=36.18°,则 ( A )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.以上都不对
A
方法归纳交流 (1)把角的度数用“度、分、秒”表示时,先把不够1度的角化为 分 ,再把不够 1分 的角化为 秒 ;把角的度数由“度、分、秒”化为“度”时,先把 秒 转化为 分 ,再把 分 化为 度 .
(2)比较几个角的大小时,如果单位不统一,应先 统一单位 ,再比较大小.
分
1分
秒
秒
分
分
度
统一单
位
角的和与差的计算
3.在同一平面上,若∠AOB=50°, ∠BOC=15°,求∠AOC的度数.
解:如图1,当OC在∠AOB外部时,∠AOC=∠AOB+∠BOC=50°+15°=65°,
如图2,当OC在∠AOB内部时,∠AOC=∠AOB-∠BOC=50°-15°=35°,
所以∠AOC的度数是65°或35°.
4.计算:(1)46°39'40″+63°41'35″;
(2)86°23'12″-67°36'50″;
(3)180°-79°19'15″.
解:(1)110°21'15″;
(2)18°46'22″;
(3)100°40'45″.
钟表中的角
7点半时,钟面上时针和分针的夹角是 45° .
45°
1下列4个角中,属于锐角的是 ( A )
A.50° B.90° C.110° D.130°
2如图,下列式子中错误的是 ( C )
A.∠AOC=∠AOB+∠BOC
B.∠AOC=∠AOD-∠COD
C.∠AOC=∠AOB+∠BOD-∠BOC
D.∠AOC=∠AOD-∠BOD+∠BOC
A
C
3按要求解题:
(1)用度、分、秒表示:①48.26°;②37.37°;
(2)用度表示:①37°24'36″;②13°37'48″.
解:(1)①48.26°=48°15'36″;②37.37°=37°22'12″;
(2)①37°24'36″=37.41°;②13°37'48″=13.63°.
4计算:(1)48°29'+67°41';(2)180°-74°13'26″.
解:(1)原式=116°10';
(2)原式=105°46'34″.
5若∠A=20°18',∠B=20°15'30″,∠C=20.25°,则( A )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
A
6如图,已知点M是直线AB上一点,∠AMC=52°48',∠BMD=72°19',则∠CMD等于 ( B )
A.49°07' B.54°53'
C.55°53' D.53°7'
B
7下列算式:①33.33°=33°3'3″;②33.33°=33°19'48″;③50°40'30″=50.43°;④50°40'30″=50.675°,其中正确的是( D )
A.①和② B.①和③
C.②和③ D.②和④
D
8如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 180 度.
180
9如图,OB平分∠AOC,∠AOD=76°.
(1)若∠BOC=20°,求∠COD的度数;
(2)若OC是∠AOD的平分线,求∠BOD的度数.
解:(1)因为OB平分∠AOC,所以∠AOC=2∠BOC=40°,所以∠COD=∠AOD-∠AOC=76°-40°=36°.
(2)因为OC是∠AOD的平分线,所以∠AOC=∠AOD=38°,因为OB平分∠AOC,所以∠AOB=∠AOC=19°,所以∠BOD=∠AOD-∠AOB=76°-19°=57°.
10(1)从1点15分到1点35分,时钟的分针与时针各转过了多大角度?
(2)1点20分时,时钟的时针与分针的夹角是几度?2点15分时,时钟的时针与分针的夹角又是几度?
解:(1)从1点15分到1点35分,分针共走了20小格.所以分针转过的角度是(35-15)×=120°,
时针转过的角度是×120°=10°.
(2)因为分针每分钟走1小格,时针每分钟走小格,
所以1点20分时,时针与分针的夹角是 20- 5+×20 ×=80°.
2点15分时,时针与分针的夹角是 15- 10+×15 ×=22.5°.
所以1点20分时,时针与分针的夹角是
×=80°.
2点15分时,时针与分针的夹角是
×=22.5°.
同课章节目录
