六年级上册数学北师大版1《生活中的比》课件(24张ppt)
文档属性
| 名称 | 六年级上册数学北师大版1《生活中的比》课件(24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-01 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
第六单元 比的认识
生活中的比
印度的泰姬陵
一、情境导入
埃及的胡夫金字塔
一、情境导入
中国故宫
一、情境导入
巴黎圣母院
一、情境导入
上海东方明珠广播电视塔
一、情境导入
西安钟楼
一、情境导入
看完之后你有什么感受呢?
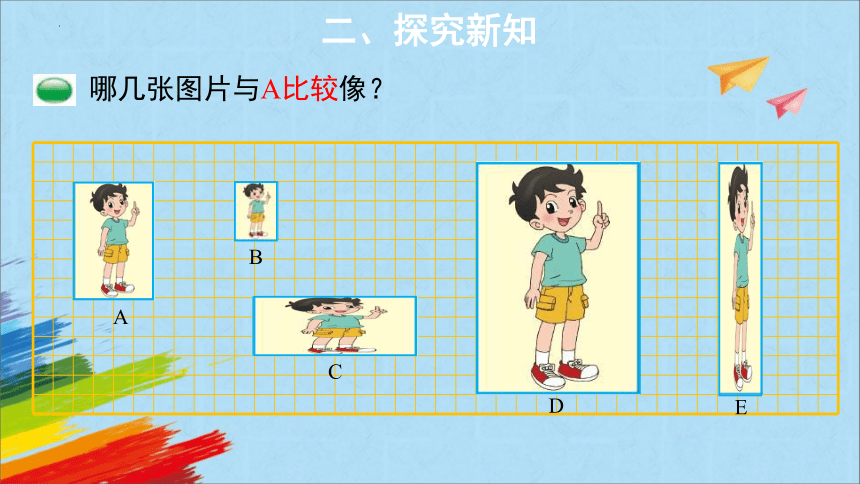
哪几张图片与A比较像?
A
B
C
D
E
二、探究新知
A
B
C
D
E
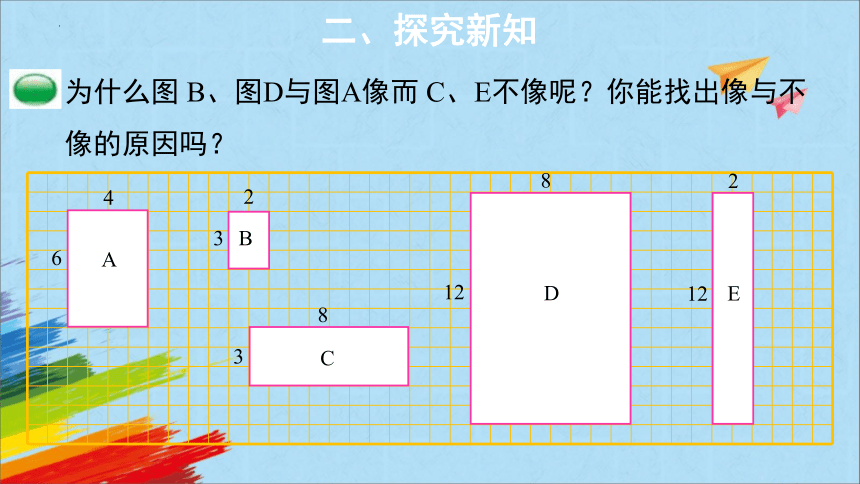
6
3
3
12
12
4
2
8
8
2
为什么图 B、图D与图A像而 C、E不像呢?你能找出像与不像的原因吗?
二、探究新知
长方形 长 宽 长是宽的几倍 宽是长的几分之几
A
B
C
D
E
二、探究新知
6
4
1.5
8
12
3
2
3
8
2
6
12
1.5
1.5
6
3
4
6
3
4
6
3
4
6
3
4
6
3
6
6
6
6
6
6
6
二、探究新知
认一认
两个数相除,又叫作这两个数的比。
6÷4
写作
6∶4
…
比号
读作
6 比 4
6∶4=6÷4= =1.5
6
4
二、探究新知
6 是这个比的前项,
4 是这个比的后项,
1.5 是 6∶4 的比值。
试一试:说出下面比的各部分名称,并求出比值。
22∶5 =
15∶3 =
3∶9 =
4.4
5
二、探究新知
比 除法 分数
前项
( ∶ ) 比号
后项
比值
(一种数)
(表示两个数的关系)
(一种运算)
比与除法、分数有什么联系与区别呢?
分子
被除数
( ÷ )
除号
(——)
分数线
分母
除数
分数值
商
=
1.5
6÷4
=
6
∶
4
=
可以是 0 吗?
=
6÷4
=
6÷4
=
1.5
=
二、探究新知
想一想
既然比的后项不能为 0,而足球比赛中常出现的 2∶0 的意义是什么?它是一个比吗?
二、探究新知
各类比赛中的比不是我们这节课学习的比,它只表示一队与另一队比赛各得的进球分数,不是表示两队所得分数的倍数关系,是比较大小的,是相差关系,不是相除关系。它虽然借用了比的写法,但它不是一个比。
4∶0
76∶77
小知识
二、探究新知
说一说下面各比的含义。
二、探究新知
路程 时间 路程与 时间的比 速度
马拉松选手 40 km 2 时
骑车人 45 km 3 时
填一填,说一说。
(1)谁快?
40∶2
45∶3
20 千米/时
15 千米/时
(2)哪种苹果最便宜?
品种 总价 数量 总价与数量的比 单价
A 9 元 2 kg
B 15 元 3 kg
C 12 元 3 kg
9∶2
4.5 元/千克
15∶3
5 元/千克
12∶3
4 元/千克
二、探究新知
人体上有许多有趣的比:
1. 婴儿的头长与身高的比大约是 1∶4。
2. 成年人的头长与身高的比约是 1∶7。
3. 身高与双臂平伸的比约是 1∶1。
4. 人的心脏与拳头的比约是 1∶1。
5. 肚脐以上与肚脐以下的比是 0.618∶1。
6. 人的脚长与身高的比 1∶7。
你能联系实际说说生活中有哪些比吗?
二、探究新知
1. 根据下列信息写出比。
女生人数与全班人数的比是 。
正方形周长与边长的比是 。
22∶40
12∶3
正方形面积与边长的比是 。
9∶3
三、巩固练习
(1)六(2)班共有40名同学,其中男生18人,女生22人。
(2)
2. 蒸包子用的面,可以用面粉 1000 g,
水 500 g,干酵母 4 汤匙(10 g),白
糖 10 g 和成。
⑴ 写出面粉和水的质量比。
⑵ 再写出两个比。
三、巩固练习
1000∶500
水和面粉的比是500∶1000;干酵母和白糖的比是10∶10。
三、巩固练习
3.如图,工人师傅用两块同样长的木板搭了两个斜坡。
斜坡A最高点的高度与木板长度的比是 ,
比值是 。
斜坡B最高点的高度与木板长度的比是 ,
比值是 。
1∶3
1
3
1∶2
1
2
四、课堂小结
通过本节课的学习我们知道了:
1. 两个数相除,又叫作这两个数的比。认识了比号“∶”,
比号前的数叫比的前项,比号后面的数叫比的后项。
2. 比与除法的关系可以用字母表示为:
a∶b = a÷b = (b≠0)。
a
b
四、课堂小结
比的意义很重要,记忆方法有技巧;
两数相除即为比,除号变点要记牢;
前后两项要对应,位置顺序不能调;
分数除法比关联,相互关系记心间。
第六单元 比的认识
生活中的比
印度的泰姬陵
一、情境导入
埃及的胡夫金字塔
一、情境导入
中国故宫
一、情境导入
巴黎圣母院
一、情境导入
上海东方明珠广播电视塔
一、情境导入
西安钟楼
一、情境导入
看完之后你有什么感受呢?
哪几张图片与A比较像?
A
B
C
D
E
二、探究新知
A
B
C
D
E
6
3
3
12
12
4
2
8
8
2
为什么图 B、图D与图A像而 C、E不像呢?你能找出像与不像的原因吗?
二、探究新知
长方形 长 宽 长是宽的几倍 宽是长的几分之几
A
B
C
D
E
二、探究新知
6
4
1.5
8
12
3
2
3
8
2
6
12
1.5
1.5
6
3
4
6
3
4
6
3
4
6
3
4
6
3
6
6
6
6
6
6
6
二、探究新知
认一认
两个数相除,又叫作这两个数的比。
6÷4
写作
6∶4
…
比号
读作
6 比 4
6∶4=6÷4= =1.5
6
4
二、探究新知
6 是这个比的前项,
4 是这个比的后项,
1.5 是 6∶4 的比值。
试一试:说出下面比的各部分名称,并求出比值。
22∶5 =
15∶3 =
3∶9 =
4.4
5
二、探究新知
比 除法 分数
前项
( ∶ ) 比号
后项
比值
(一种数)
(表示两个数的关系)
(一种运算)
比与除法、分数有什么联系与区别呢?
分子
被除数
( ÷ )
除号
(——)
分数线
分母
除数
分数值
商
=
1.5
6÷4
=
6
∶
4
=
可以是 0 吗?
=
6÷4
=
6÷4
=
1.5
=
二、探究新知
想一想
既然比的后项不能为 0,而足球比赛中常出现的 2∶0 的意义是什么?它是一个比吗?
二、探究新知
各类比赛中的比不是我们这节课学习的比,它只表示一队与另一队比赛各得的进球分数,不是表示两队所得分数的倍数关系,是比较大小的,是相差关系,不是相除关系。它虽然借用了比的写法,但它不是一个比。
4∶0
76∶77
小知识
二、探究新知
说一说下面各比的含义。
二、探究新知
路程 时间 路程与 时间的比 速度
马拉松选手 40 km 2 时
骑车人 45 km 3 时
填一填,说一说。
(1)谁快?
40∶2
45∶3
20 千米/时
15 千米/时
(2)哪种苹果最便宜?
品种 总价 数量 总价与数量的比 单价
A 9 元 2 kg
B 15 元 3 kg
C 12 元 3 kg
9∶2
4.5 元/千克
15∶3
5 元/千克
12∶3
4 元/千克
二、探究新知
人体上有许多有趣的比:
1. 婴儿的头长与身高的比大约是 1∶4。
2. 成年人的头长与身高的比约是 1∶7。
3. 身高与双臂平伸的比约是 1∶1。
4. 人的心脏与拳头的比约是 1∶1。
5. 肚脐以上与肚脐以下的比是 0.618∶1。
6. 人的脚长与身高的比 1∶7。
你能联系实际说说生活中有哪些比吗?
二、探究新知
1. 根据下列信息写出比。
女生人数与全班人数的比是 。
正方形周长与边长的比是 。
22∶40
12∶3
正方形面积与边长的比是 。
9∶3
三、巩固练习
(1)六(2)班共有40名同学,其中男生18人,女生22人。
(2)
2. 蒸包子用的面,可以用面粉 1000 g,
水 500 g,干酵母 4 汤匙(10 g),白
糖 10 g 和成。
⑴ 写出面粉和水的质量比。
⑵ 再写出两个比。
三、巩固练习
1000∶500
水和面粉的比是500∶1000;干酵母和白糖的比是10∶10。
三、巩固练习
3.如图,工人师傅用两块同样长的木板搭了两个斜坡。
斜坡A最高点的高度与木板长度的比是 ,
比值是 。
斜坡B最高点的高度与木板长度的比是 ,
比值是 。
1∶3
1
3
1∶2
1
2
四、课堂小结
通过本节课的学习我们知道了:
1. 两个数相除,又叫作这两个数的比。认识了比号“∶”,
比号前的数叫比的前项,比号后面的数叫比的后项。
2. 比与除法的关系可以用字母表示为:
a∶b = a÷b = (b≠0)。
a
b
四、课堂小结
比的意义很重要,记忆方法有技巧;
两数相除即为比,除号变点要记牢;
前后两项要对应,位置顺序不能调;
分数除法比关联,相互关系记心间。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
