人教版八年级上册 第十二章全等基础模型课件(共19张PPT)
文档属性
| 名称 | 人教版八年级上册 第十二章全等基础模型课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 676.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第十二章 全等三角形
专题四 模型拓展——全等基础模型
目录
01
模型解读
02
针对训练
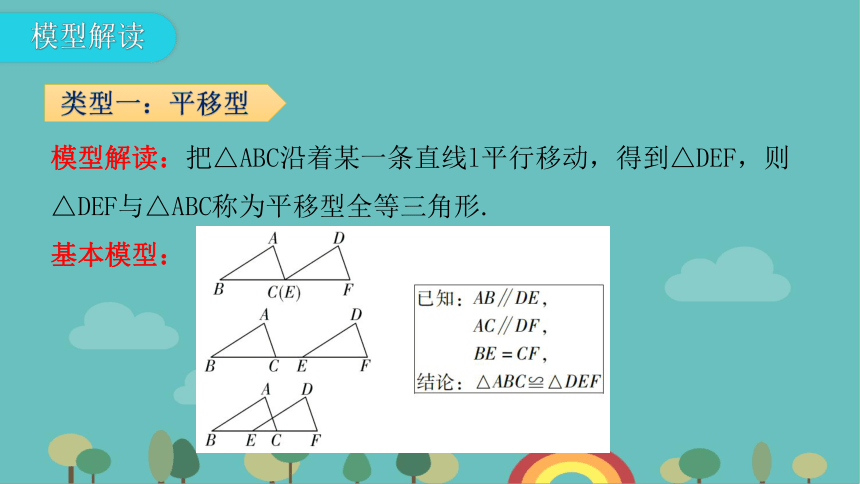
类型一:平移型
模型解读
模型解读:把△ABC沿着某一条直线l平行移动,得到△DEF,则△DEF与△ABC称为平移型全等三角形.
基本模型:
针对训练
1.如图Z12-4-1,点O是线段AB的中点,OD∥BC且OD=BC.若∠ADO=35°,求∠DOC的度数.
模型解读
类型二:翻折型
模型解读:将原图形沿着某一条直线折叠后,直线两边的部分能够完全重合,这两个三角形称之为翻折型全等三角形.此类图形中要注意其隐含条件,即公共边或公共角相等.
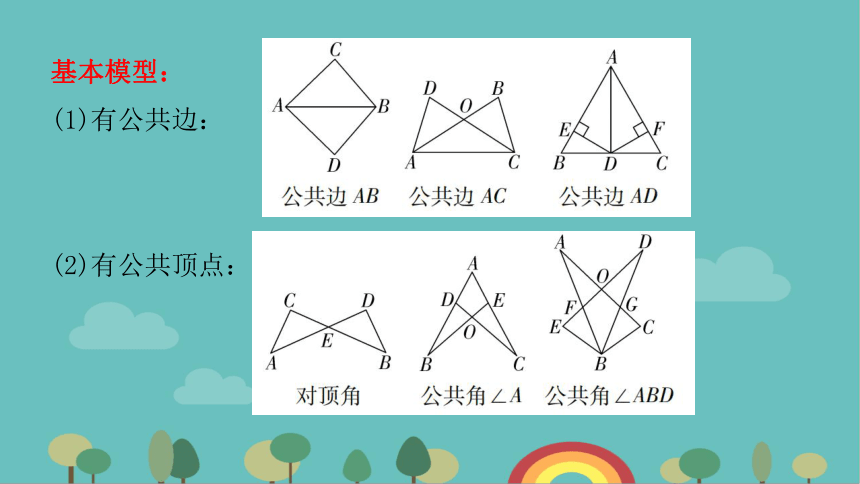
基本模型:
(1)有公共边:
(2)有公共顶点:
针对训练
2.如图Z12-4-2,已知AC=BC,∠1=∠2,求证:OD平分∠AOB.
3.如图Z12-4-3,已知AB=AC,BE⊥AC于点E,CD⊥AB于点D.求证:AD=AE.
模型解读
类型三:旋转型
模型解读:将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全重合,则称这两个三角形为旋转型三角形.识别旋转型三角形时,注意涉及对顶角相等或者等角加(减)公共角的条件.
基本模型:
(1)共顶点:
(2)不共顶点:
针对训练
4.如图Z12-4-4,在△ABC和△AEF中,点E在BC边上,∠C=∠F,AC=AF,∠CAF=∠BAE,EF与AC交于点G.求证:AE=AB.
5.如图Z12-4-5,点C,E,F,B在同一条直线上,CE=BF,AB=DC且AB∥DC.求证:∠A=∠D.
模型解读
类型四: 三垂直型
模型解读:常用三个垂直作条件进行角度等量代换,即同(等)角的余角相等,相等的角就是对应角,证三角形全等时必须还有一组边相等.
基本模型:
(1)一线三垂直型:
(2)三个直角不在同一直线上:
已知:AB⊥BC,
DC⊥BC,
AE⊥BD,
AB=BC,
结论:△ABE≌△BCD,
CE=AB-CD
已知:AB⊥BC,
CD⊥BD,
AE⊥BD,
AB=BC,
结论:△ABE≌△BCD,
DE=AE-CD
针对训练
6.如图Z12-4-6,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5 cm,求AE的长.
谢 谢
第十二章 全等三角形
专题四 模型拓展——全等基础模型
目录
01
模型解读
02
针对训练
类型一:平移型
模型解读
模型解读:把△ABC沿着某一条直线l平行移动,得到△DEF,则△DEF与△ABC称为平移型全等三角形.
基本模型:
针对训练
1.如图Z12-4-1,点O是线段AB的中点,OD∥BC且OD=BC.若∠ADO=35°,求∠DOC的度数.
模型解读
类型二:翻折型
模型解读:将原图形沿着某一条直线折叠后,直线两边的部分能够完全重合,这两个三角形称之为翻折型全等三角形.此类图形中要注意其隐含条件,即公共边或公共角相等.
基本模型:
(1)有公共边:
(2)有公共顶点:
针对训练
2.如图Z12-4-2,已知AC=BC,∠1=∠2,求证:OD平分∠AOB.
3.如图Z12-4-3,已知AB=AC,BE⊥AC于点E,CD⊥AB于点D.求证:AD=AE.
模型解读
类型三:旋转型
模型解读:将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全重合,则称这两个三角形为旋转型三角形.识别旋转型三角形时,注意涉及对顶角相等或者等角加(减)公共角的条件.
基本模型:
(1)共顶点:
(2)不共顶点:
针对训练
4.如图Z12-4-4,在△ABC和△AEF中,点E在BC边上,∠C=∠F,AC=AF,∠CAF=∠BAE,EF与AC交于点G.求证:AE=AB.
5.如图Z12-4-5,点C,E,F,B在同一条直线上,CE=BF,AB=DC且AB∥DC.求证:∠A=∠D.
模型解读
类型四: 三垂直型
模型解读:常用三个垂直作条件进行角度等量代换,即同(等)角的余角相等,相等的角就是对应角,证三角形全等时必须还有一组边相等.
基本模型:
(1)一线三垂直型:
(2)三个直角不在同一直线上:
已知:AB⊥BC,
DC⊥BC,
AE⊥BD,
AB=BC,
结论:△ABE≌△BCD,
CE=AB-CD
已知:AB⊥BC,
CD⊥BD,
AE⊥BD,
AB=BC,
结论:△ABE≌△BCD,
DE=AE-CD
针对训练
6.如图Z12-4-6,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5 cm,求AE的长.
谢 谢
