圆的基本性质检测试题
图片预览

文档简介
圆的基本性质检测题
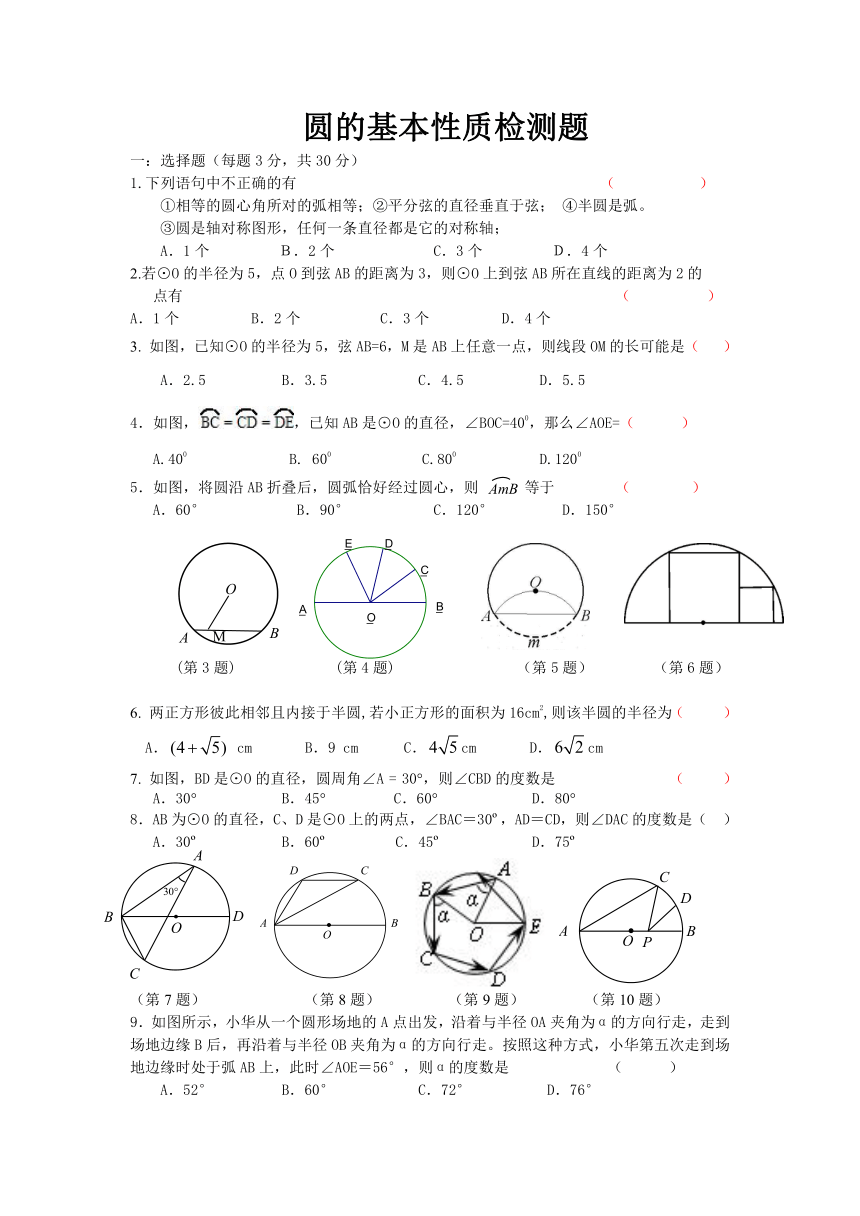
一:选择题(每题3分,共30分)
1.下列语句中不正确的有 ( )
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦; ④半圆是弧。
③圆是轴对称图形,任何一条直径都是它的对称轴;
A.1个 B.2个 C.3个 D.4个
2.若⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的
点有 ( )
A.1个 B.2个 C.3个 D.4个
3. 如图,已知⊙O的半径为5,弦AB=6,M是AB上任意一点,则线段OM的长可能是( )
A.2.5 B.3.5 C.4.5 D.5.5
4.如图, ( http: / / www. / Index.html ),已知AB是⊙O的直径, ( http: / / )∠BOC=400,那么∠AOE=( )
A.400 B. 600 C.800 D.1200
5.如图,将圆沿AB折叠后,圆弧恰好经过圆心,则 等于 ( )
A.60° B.90° C.120° D.150°
(第3题) (第4题) (第5题) (第6题)
6. 两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A. cm B.9 cm C.cm D.cm
7. 如图,BD是⊙O的直径,圆周角∠A = 30,则∠CBD的度数是 ( )
A.30 B.45 C.60 D.80
8.AB为⊙O的直径,C、D是⊙O上的两点,∠BAC=30 ,AD=CD,则∠DAC的度数是( )
A.30 B.60 C.45 D.75
(第7题) (第8题) (第9题) (第10题)
9.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向行走。按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是 ( )
A.52° B.60° C.72° D.76°
10.如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为 的中点,P是直径
AB上一动点,则PC+PD的最小值为 ( )
A. B. C. D.
二:填空题(每题4分,共24分)
11. 如图,⊙O的半径OA=10cm,弦AB=16cm,P为AB上一动点,则点P到圆心O的最短距
离为 。
12. 一条弦把圆分为2∶3的两部分,那么这条弦所对的圆周角度数为 。
13. 如图,CD是⊙O的直径,弦AB⊥CD,若∠AOB=100°,则∠ABD = 。
14.点A、B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合)连结AP,
PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF= 。
15. 如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦
AB的长是 。
(第11题) (第13题) (第14题) (第15题)
16. 在半径为5cm的圆中,两条平行弦的长度分别为6cm和8cm,则这两条弦之间的距离为 .
三:解答题(共66分)
17. 如图所示,⊙O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求CD。
18. 如图所示,是⊙O的一条弦,,垂足为,交⊙O于点D,点在⊙O上。(1)若,求的度数;(2)若,,求的长。
19. 如图所示,已知AB为⊙O的直径,CD是弦,且ABCD于点E。连接AC、OC、BC。
(1)求证:ACO=BCD。(2)若EB=,CD=,求⊙O的面积。
20. 如图,在⊙O中,=2 ,试判断AB与CD的大小关系,并说明理由。
21. 如图,BC为⊙O的直径,AD⊥BC,垂足为D。若AB与AF两弧相等,BF和AD相交于E。试猜想AE与BE的长度之间的关系,并请说明理由。
22. 如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D。⑴求证:PB=PD。⑵若角的顶点P在圆上或圆内,⑴中的结论还成立吗?若不成立,请说明理由;若成立,请加以证明。(画出相关图形)
23. 如图,P是⊙O外一点,PAB、PCD分别与⊙O相交于A、B、C、D.(1)PO平分∠BPD;(2)AB=CD;(3)OE⊥CD,OF⊥AB;(4)OE=OF.从中选出两个作为条件,另两个作为结论组成一个真命题,并加以证明.
24. 如图,⊙O半径为2,直径CD以O为中心,在⊙O所在平面内转动,当CD 转动时,OA固定不动,0°≤∠DOA≤90°,且总有BC∥OA,AB∥CD,若OA=4,BC与⊙O交于E,连AD,设CE为x,四边形ABCD的面积为y。(1)求y关于x的函数解析式,并指出x的取值范围;(2)当x=2时,求四边形ABCD在圆内的面积与四边形ABCD的面积之比;3)当x取何值时,四边形ABCD为直角梯形?连EF,此时OCEF变成什么图形?(只说结论,不必证明)。
已知:如图,ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD
求证。 (1)AP=PD;
(2)请判断A,D,F三点是否在以P为圆心,以PD为半径的圆上?并说明理由;
(3)连接CD,若CD﹦3,BD ﹦4,求⊙O的半径和DE的长.
26, .如图1,中,AB=AC,BD是的平分线,A、B、D三点的圆与BC相交于点E,你认为AD=CE吗?如果不能,请举反例;如果AD=CE,请说明理由.
AmB
_
O
_
E
_
D
_
C
_
B
_
A
A
B
O
M
O
30
D
B
C
A
A
O
P
B
D
C
O
D
C
B
A
A
E
O
F
B
P
A
D
B
C
O
O
E
D
C
B
A
E
B
D
C
A
O
BD
E
D
B
A
O
C
C
B
A
O
D
F
E
C
B
A
O
D
C
E
B
A
D
O
F
A
B
C
D
E
O
F
P
一:选择题(每题3分,共30分)
1.下列语句中不正确的有 ( )
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦; ④半圆是弧。
③圆是轴对称图形,任何一条直径都是它的对称轴;
A.1个 B.2个 C.3个 D.4个
2.若⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的
点有 ( )
A.1个 B.2个 C.3个 D.4个
3. 如图,已知⊙O的半径为5,弦AB=6,M是AB上任意一点,则线段OM的长可能是( )
A.2.5 B.3.5 C.4.5 D.5.5
4.如图, ( http: / / www. / Index.html ),已知AB是⊙O的直径, ( http: / / )∠BOC=400,那么∠AOE=( )
A.400 B. 600 C.800 D.1200
5.如图,将圆沿AB折叠后,圆弧恰好经过圆心,则 等于 ( )
A.60° B.90° C.120° D.150°
(第3题) (第4题) (第5题) (第6题)
6. 两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A. cm B.9 cm C.cm D.cm
7. 如图,BD是⊙O的直径,圆周角∠A = 30,则∠CBD的度数是 ( )
A.30 B.45 C.60 D.80
8.AB为⊙O的直径,C、D是⊙O上的两点,∠BAC=30 ,AD=CD,则∠DAC的度数是( )
A.30 B.60 C.45 D.75
(第7题) (第8题) (第9题) (第10题)
9.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向行走。按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是 ( )
A.52° B.60° C.72° D.76°
10.如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为 的中点,P是直径
AB上一动点,则PC+PD的最小值为 ( )
A. B. C. D.
二:填空题(每题4分,共24分)
11. 如图,⊙O的半径OA=10cm,弦AB=16cm,P为AB上一动点,则点P到圆心O的最短距
离为 。
12. 一条弦把圆分为2∶3的两部分,那么这条弦所对的圆周角度数为 。
13. 如图,CD是⊙O的直径,弦AB⊥CD,若∠AOB=100°,则∠ABD = 。
14.点A、B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合)连结AP,
PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF= 。
15. 如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦
AB的长是 。
(第11题) (第13题) (第14题) (第15题)
16. 在半径为5cm的圆中,两条平行弦的长度分别为6cm和8cm,则这两条弦之间的距离为 .
三:解答题(共66分)
17. 如图所示,⊙O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求CD。
18. 如图所示,是⊙O的一条弦,,垂足为,交⊙O于点D,点在⊙O上。(1)若,求的度数;(2)若,,求的长。
19. 如图所示,已知AB为⊙O的直径,CD是弦,且ABCD于点E。连接AC、OC、BC。
(1)求证:ACO=BCD。(2)若EB=,CD=,求⊙O的面积。
20. 如图,在⊙O中,=2 ,试判断AB与CD的大小关系,并说明理由。
21. 如图,BC为⊙O的直径,AD⊥BC,垂足为D。若AB与AF两弧相等,BF和AD相交于E。试猜想AE与BE的长度之间的关系,并请说明理由。
22. 如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D。⑴求证:PB=PD。⑵若角的顶点P在圆上或圆内,⑴中的结论还成立吗?若不成立,请说明理由;若成立,请加以证明。(画出相关图形)
23. 如图,P是⊙O外一点,PAB、PCD分别与⊙O相交于A、B、C、D.(1)PO平分∠BPD;(2)AB=CD;(3)OE⊥CD,OF⊥AB;(4)OE=OF.从中选出两个作为条件,另两个作为结论组成一个真命题,并加以证明.
24. 如图,⊙O半径为2,直径CD以O为中心,在⊙O所在平面内转动,当CD 转动时,OA固定不动,0°≤∠DOA≤90°,且总有BC∥OA,AB∥CD,若OA=4,BC与⊙O交于E,连AD,设CE为x,四边形ABCD的面积为y。(1)求y关于x的函数解析式,并指出x的取值范围;(2)当x=2时,求四边形ABCD在圆内的面积与四边形ABCD的面积之比;3)当x取何值时,四边形ABCD为直角梯形?连EF,此时OCEF变成什么图形?(只说结论,不必证明)。
已知:如图,ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD
求证。 (1)AP=PD;
(2)请判断A,D,F三点是否在以P为圆心,以PD为半径的圆上?并说明理由;
(3)连接CD,若CD﹦3,BD ﹦4,求⊙O的半径和DE的长.
26, .如图1,中,AB=AC,BD是的平分线,A、B、D三点的圆与BC相交于点E,你认为AD=CE吗?如果不能,请举反例;如果AD=CE,请说明理由.
AmB
_
O
_
E
_
D
_
C
_
B
_
A
A
B
O
M
O
30
D
B
C
A
A
O
P
B
D
C
O
D
C
B
A
A
E
O
F
B
P
A
D
B
C
O
O
E
D
C
B
A
E
B
D
C
A
O
BD
E
D
B
A
O
C
C
B
A
O
D
F
E
C
B
A
O
D
C
E
B
A
D
O
F
A
B
C
D
E
O
F
P
同课章节目录
