4.1圆的对称性---垂径定理

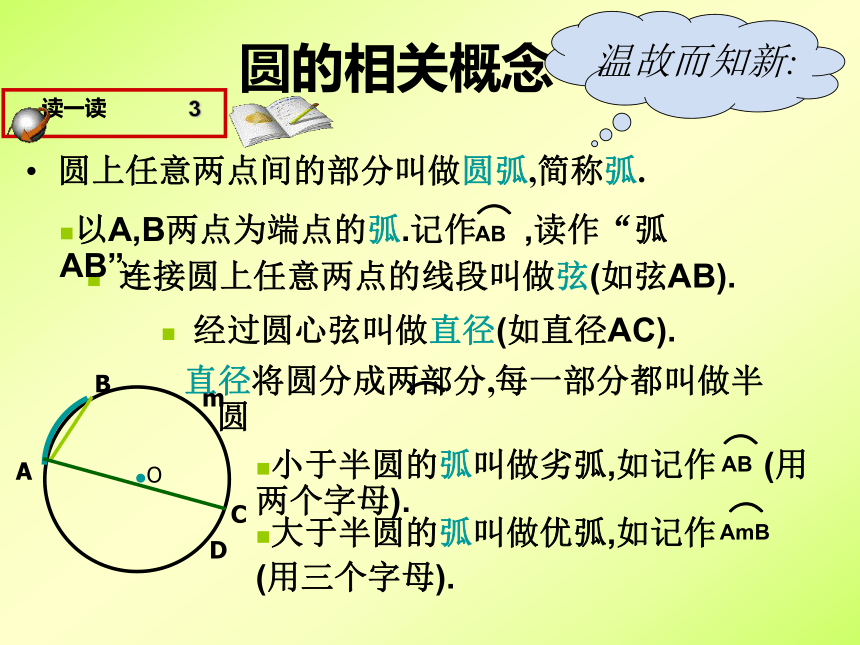
课件18张PPT。九年级数学(上)第四章： 对圆的进一步认识驶向胜利的彼岸4.1圆的对称性--垂径定理圆的相关概念圆上任意两点间的部分叫做圆弧,简称弧.直径将圆分成两部分,每一部分都叫做半圆 连接圆上任意两点的线段叫做弦(如弦AB).经过圆心弦叫做直径(如直径AC).⌒Company Logo学习目标1、会利用圆的轴对称性探究垂径定理、证明垂径定理；
2、能利用垂径定理进行相关的计算和证明；
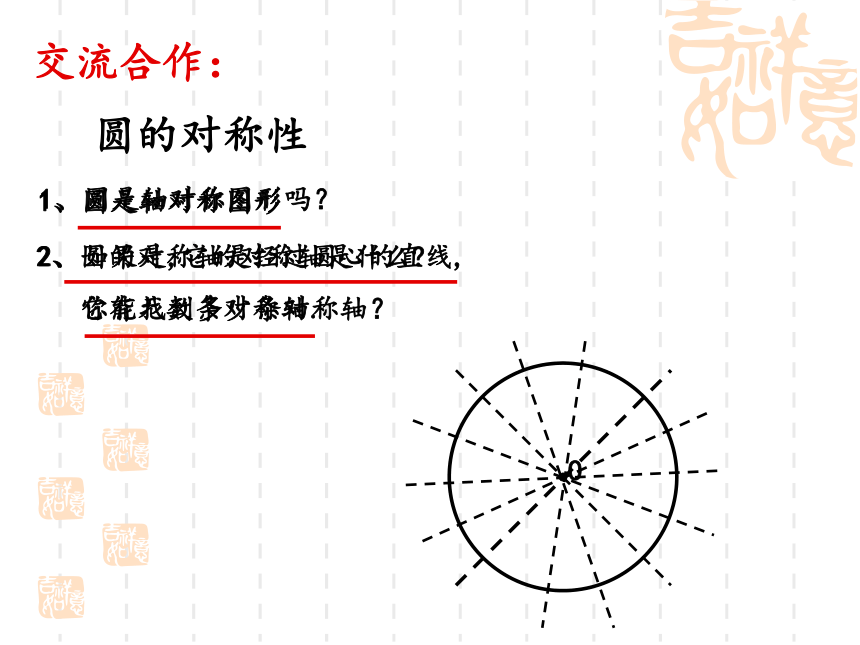
3、掌握垂径定理的推论。圆的对称性1、圆是轴对称图形吗？2、如果是,它的对称轴是什么?
你能找到多少条对称轴？1、圆是轴对称图形2、圆的对称轴是经过圆心的直线,
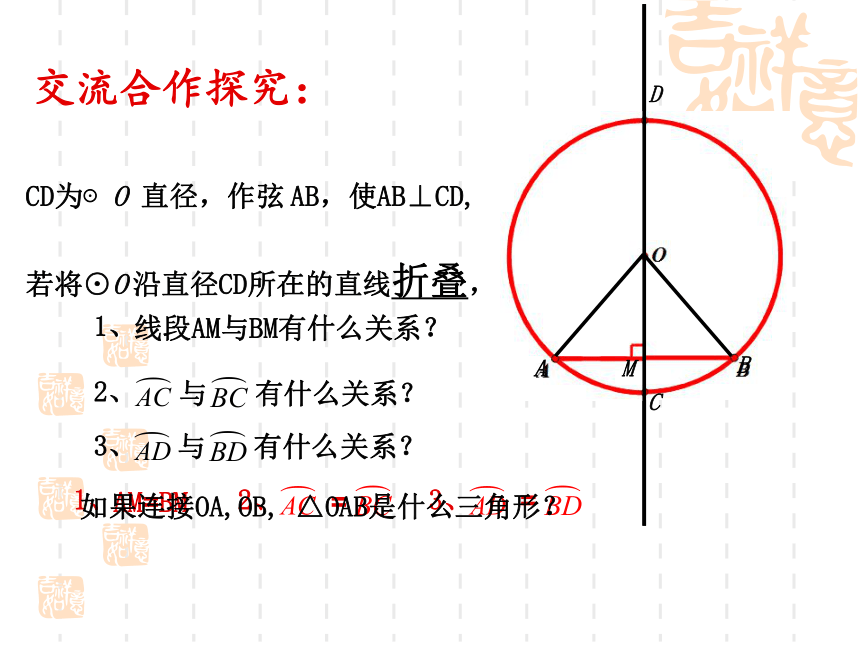
它有无数条对称轴.交流合作：DCD为⊙O 直径，作弦 AB，使AB⊥CD,
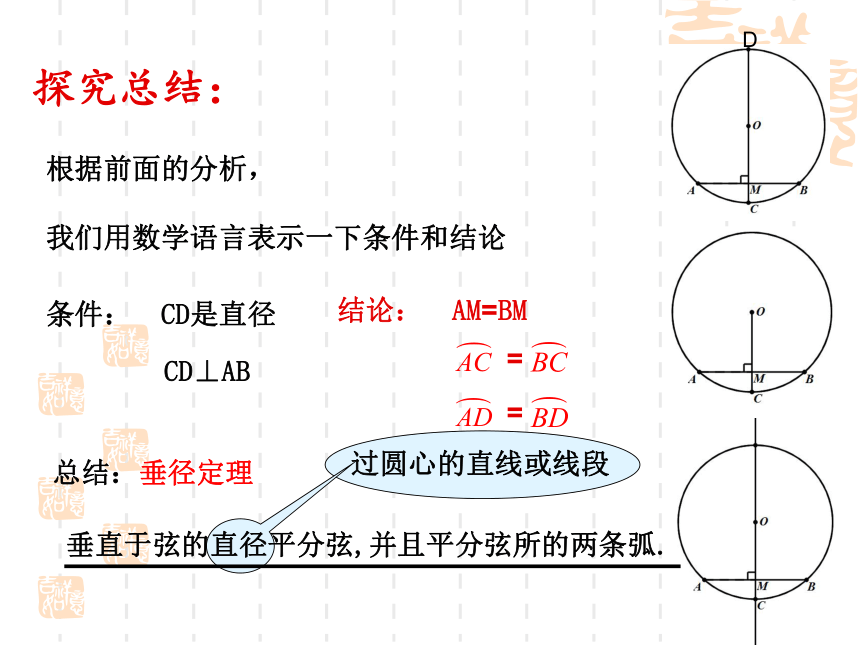
若将⊙O 沿直径CD所在的直线折叠，C交流合作探究：M如果连接OA,OB, △OAB是什么三角形？探究总结：根据前面的分析，
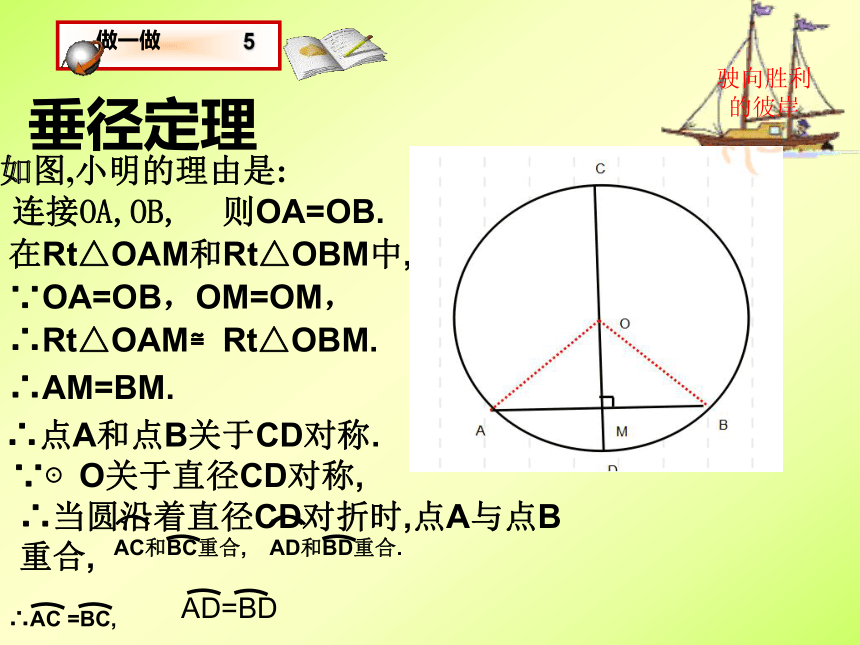
我们用数学语言表示一下条件和结论总结：垂径定理过圆心的直线或线段D垂径定理如图,小明的理由是:连接OA,OB,驶向胜利的彼岸则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB，OM=OM，∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,AD=BD垂径定理的推论1：平分弦（不是直径）的直径垂直于这条弦，并且平分弦所对的两条弧。思考：如果CD是⊙O的弦（不是直径），过CD的中点E作⊙O的直径AB。你发现AB与CD互相垂直吗？BC与BD的大小有什么关系？AC与AD的大小有什么关系？想一想：为什么这里强调CD是⊙O的弦而不是直径呢？你可以写出相应的命题吗?
相信自己是最棒的!垂径定理的逆定理如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,问题1：弦的垂直平分线一定过圆心吗？你还能得到什么结论？问题2:(如图)AB,CD为⊙O的弦，
你能确定圆心的位置吗？交流合作：典例应用 例1、1300多年前，我国隋代建造的赵州石拱桥是圆弧形，它的跨度（弧所对的弦长）为37.4m，拱高（弧的中点到弦的距离，也叫弓形的高）为7.2m。
求桥拱的半径。？勾股定理分析：注意过程的写法！画一画1、如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.
并且AM=BM.挑战自我 2.已知：如图,⊙O 中,弦AB∥CD,AB＜CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有
图中相等的劣弧有:3、已知：如图，⊙O 中，AB为弦，C为 的中点，OC交 AB于D，AB = 6cm ，CD = 1cm ，求⊙O 的半径OA.等腰三角形的性质及勾股定理在圆的有关计算中应用非常广泛① 垂径定理： ② 如何判断圆的圆心的位置 ③ 在解有关题目的时候，
常利用直角三角形的勾股定理！谈
收
获弦的垂直平分线必定经过圆心！知识的升华鲜花为你盛开，你一定行！习题4.1 A组
2，3题结束寄语不学自知,不问自晓,古今行事,未之有也.再见