用三种方式表示二次函数[上学期]
图片预览

文档简介
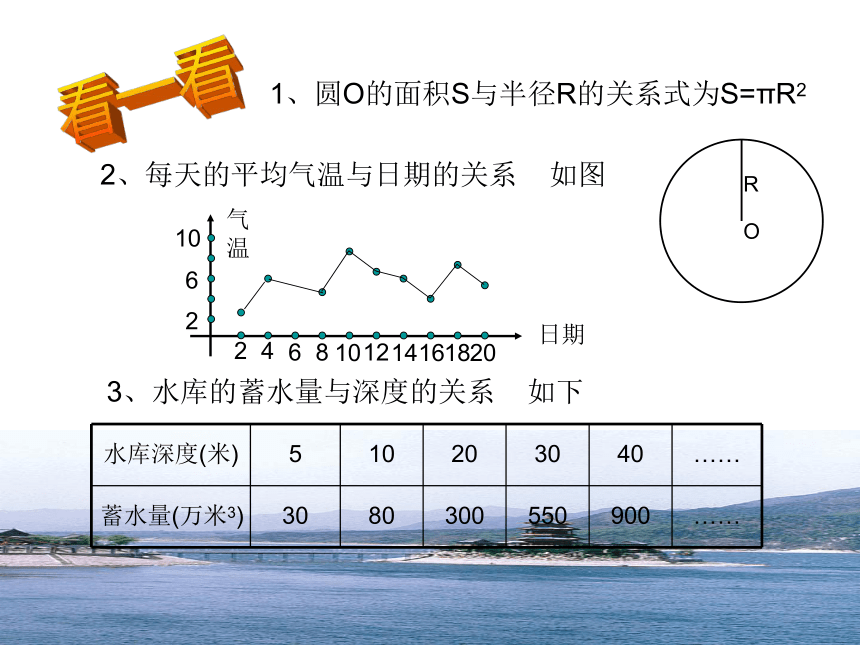
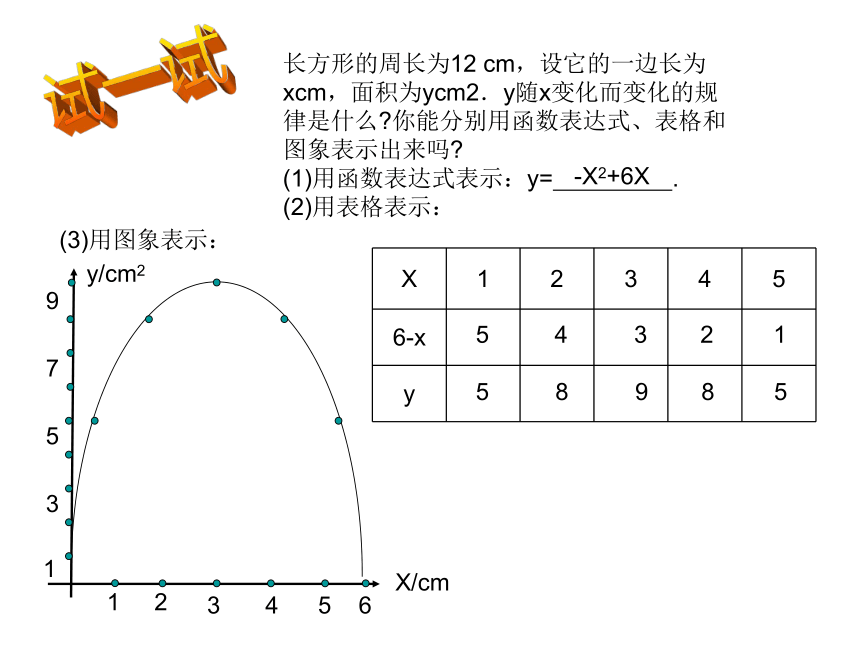
课件10张PPT。用三种方式表示二次函数兰溪二中 叶光平看一看1、圆O的面积S与半径R的关系式为S=πR22、每天的平均气温与日期的关系 如图3、水库的蓄水量与深度的关系 如下长方形的周长为12 cm,设它的一边长为xcm,面积为ycm2.y随x变化而变化的规律是什么?你能分别用函数表达式、表格和图象表示出来吗?
(1)用函数表达式表示:y= .
(2)用表格表示:试一试(3)用图象表示:-X2+6X 4 3 2 1
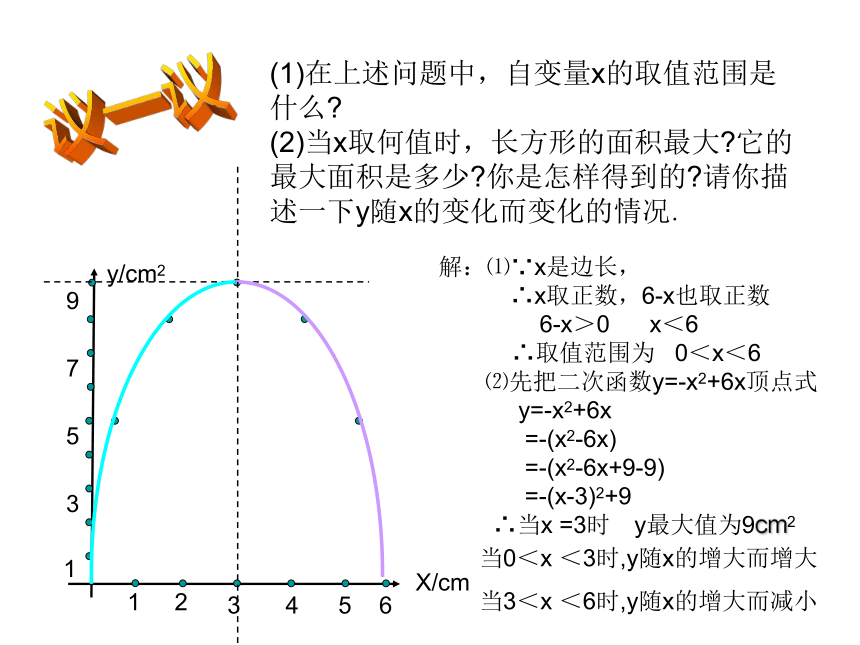
5 8 9 8 5X/cmy/cm212345135796(1)在上述问题中,自变量x的取值范围是什么?
(2)当x取何值时,长方形的面积最大?它的最大面积是多少?你是怎样得到的?请你描述一下y随x的变化而变化的情况.议一议X/cmy/cm212345135796解:⑴∵x是边长,
∴x取正数,6-x也取正数
6-x>0 x<6
∴取值范围为 0<x<6
⑵先把二次函数y=-x2+6x顶点式
y=-x2+6x
=-(x2-6x)
=-(x2-6x+9-9)
=-(x-3)2+9
∴当x =3时 y最大值为9cm2当0<x <3时,y随x的增大而增大
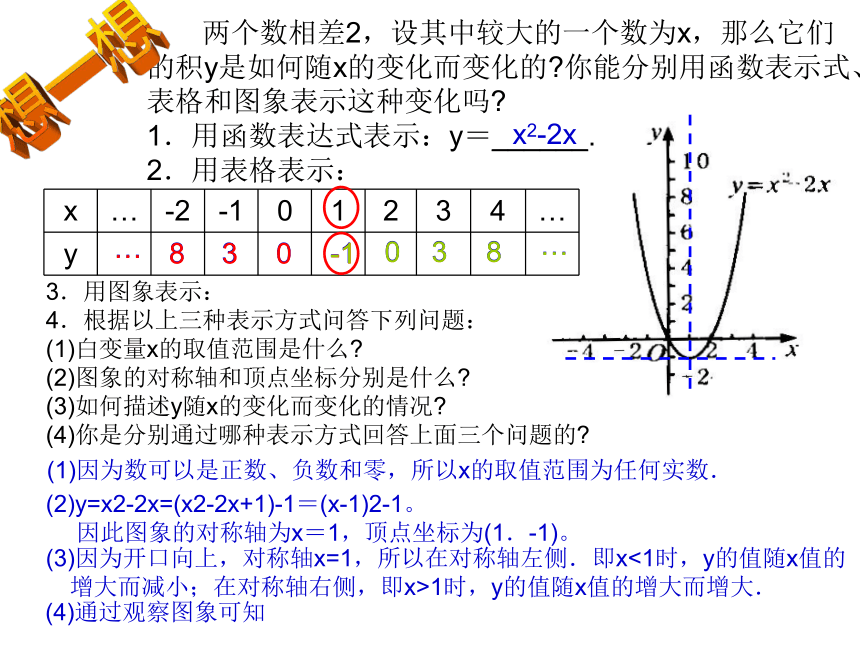
当3<x <6时,y随x的增大而减小 两个数相差2,设其中较大的一个数为x,那么它们的积y是如何随x的变化而变化的?你能分别用函数表示式、表格和图象表示这种变化吗?
1.用函数表达式表示:y=______.
2.用表格表示:3.用图象表示:
4.根据以上三种表示方式问答下列问题:
(1)白变量x的取值范围是什么?
(2)图象的对称轴和顶点坐标分别是什么?
(3)如何描述y随x的变化而变化的情况?
(4)你是分别通过哪种表示方式回答上面三个问题的?x2-2x(2)y=x2-2x=(x2-2x+1)-1=(x-1)2-1。
因此图象的对称轴为x=1,顶点坐标为(1.-1)。(1)因为数可以是正数、负数和零,所以x的取值范围为任何实数.(3)因为开口向上,对称轴x=1,所以在对称轴左侧.即x<1时,y的值随x值的
增大而减小;在对称轴右侧,即x>1时,y的值随x值的增大而增大.(4)通过观察图象可知想一想议一议函数的表格表示可以清楚、直接地表示出变量之间
的数值对应关系;
函数的图象表示可以直观地表示出函数的变化过程
和变化趋势;
函数的表达式可以比较全面、完整、简洁地表示出
变量之间的关系,
这三种表示方式各自有各自的优点,它们服务于不同的需要.
它们的联系是三种方式可以互化,由表达式可转化为表格和图象表示,每一种方式都可转化为另两种方式表示.二次函数的三种表示方式有什么特点?它们之间有什么联系?与同伴进行交流.三种表示方式必须考虑自变量的取值范围 !三种表示方式的关系流程图表格表示图像表示表达式 (1)你知道上面每一个图形中各有多少个小圆圈吗?第6个图形中应该有多少个小圆圈?为什么?
(2)完成下表:边上的小圆圈数12345小圆圈的总数
(3)如果用n表示等边三角形边上的小圆圈数,m表示这个三角形中小圆圈的总数,那么m和n的关系是什么?
解:(1)观察前5个图形可知,第2个图形比第1个多2个小圆圈,第3个比第2个多3个,第4个比第3个多4个,第5个比第4个多5个,据此第6个应比第5个多6个小圆圈,因此第6个图形应该有21个小圆圈.
(3) 1=1 3=1+2 6=1+2+3 10=1+2+3+4 ……
m=1+2+3+4+ ……+n=练一练1 3 6 10 152.(1)你知道下面每一个图形中各有多少个圆圈吗?为什么?
(2)完成下表;(3)如果用n表示六边形边上的小圆圈数,m表示这个六边形中小圆圈的总数,那么m和n的关系是什么?课后活动与探究 1.长度为120米的竹篱笆一面靠墙围成一个矩形养鸡场,墙长50米,设宽为x米长为y米,求y关于x的表达式____,x取值范围为_____xy感谢各位老师的光临指导!谢谢同学们的配合!再见
(1)用函数表达式表示:y= .
(2)用表格表示:试一试(3)用图象表示:-X2+6X 4 3 2 1
5 8 9 8 5X/cmy/cm212345135796(1)在上述问题中,自变量x的取值范围是什么?
(2)当x取何值时,长方形的面积最大?它的最大面积是多少?你是怎样得到的?请你描述一下y随x的变化而变化的情况.议一议X/cmy/cm212345135796解:⑴∵x是边长,
∴x取正数,6-x也取正数
6-x>0 x<6
∴取值范围为 0<x<6
⑵先把二次函数y=-x2+6x顶点式
y=-x2+6x
=-(x2-6x)
=-(x2-6x+9-9)
=-(x-3)2+9
∴当x =3时 y最大值为9cm2当0<x <3时,y随x的增大而增大
当3<x <6时,y随x的增大而减小 两个数相差2,设其中较大的一个数为x,那么它们的积y是如何随x的变化而变化的?你能分别用函数表示式、表格和图象表示这种变化吗?
1.用函数表达式表示:y=______.
2.用表格表示:3.用图象表示:
4.根据以上三种表示方式问答下列问题:
(1)白变量x的取值范围是什么?
(2)图象的对称轴和顶点坐标分别是什么?
(3)如何描述y随x的变化而变化的情况?
(4)你是分别通过哪种表示方式回答上面三个问题的?x2-2x(2)y=x2-2x=(x2-2x+1)-1=(x-1)2-1。
因此图象的对称轴为x=1,顶点坐标为(1.-1)。(1)因为数可以是正数、负数和零,所以x的取值范围为任何实数.(3)因为开口向上,对称轴x=1,所以在对称轴左侧.即x<1时,y的值随x值的
增大而减小;在对称轴右侧,即x>1时,y的值随x值的增大而增大.(4)通过观察图象可知想一想议一议函数的表格表示可以清楚、直接地表示出变量之间
的数值对应关系;
函数的图象表示可以直观地表示出函数的变化过程
和变化趋势;
函数的表达式可以比较全面、完整、简洁地表示出
变量之间的关系,
这三种表示方式各自有各自的优点,它们服务于不同的需要.
它们的联系是三种方式可以互化,由表达式可转化为表格和图象表示,每一种方式都可转化为另两种方式表示.二次函数的三种表示方式有什么特点?它们之间有什么联系?与同伴进行交流.三种表示方式必须考虑自变量的取值范围 !三种表示方式的关系流程图表格表示图像表示表达式 (1)你知道上面每一个图形中各有多少个小圆圈吗?第6个图形中应该有多少个小圆圈?为什么?
(2)完成下表:边上的小圆圈数12345小圆圈的总数
(3)如果用n表示等边三角形边上的小圆圈数,m表示这个三角形中小圆圈的总数,那么m和n的关系是什么?
解:(1)观察前5个图形可知,第2个图形比第1个多2个小圆圈,第3个比第2个多3个,第4个比第3个多4个,第5个比第4个多5个,据此第6个应比第5个多6个小圆圈,因此第6个图形应该有21个小圆圈.
(3) 1=1 3=1+2 6=1+2+3 10=1+2+3+4 ……
m=1+2+3+4+ ……+n=练一练1 3 6 10 152.(1)你知道下面每一个图形中各有多少个圆圈吗?为什么?
(2)完成下表;(3)如果用n表示六边形边上的小圆圈数,m表示这个六边形中小圆圈的总数,那么m和n的关系是什么?课后活动与探究 1.长度为120米的竹篱笆一面靠墙围成一个矩形养鸡场,墙长50米,设宽为x米长为y米,求y关于x的表达式____,x取值范围为_____xy感谢各位老师的光临指导!谢谢同学们的配合!再见
