人教版八年级上册14.2.乘法公式课件(共30张PPT)
文档属性
| 名称 | 人教版八年级上册14.2.乘法公式课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 198.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 19:21:15 | ||
图片预览





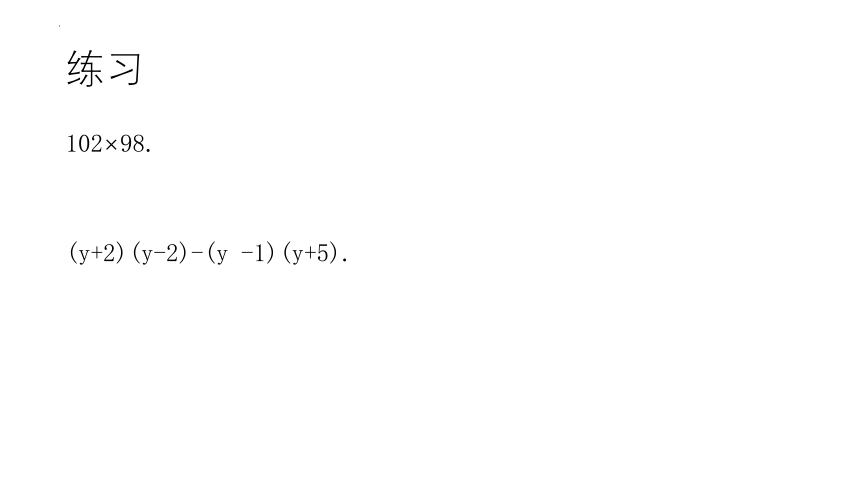




文档简介
(共30张PPT)
14.2 乘法公式
复习
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn.
活动
1. (x+1)(x-1); 2. (a+2)(a-2);
3. (3-x)(3+x) ; 4. (2x+1)(2x-1).
观察上述算式,你能发现什么规律?运算出结果后,你又发现什么规律?
平方差公式
(a+b)(a- b)=a2- ab+ab- b2= a2- b2.
即两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式的逆用: a2-b2 = (a+b)(a-b)
证明
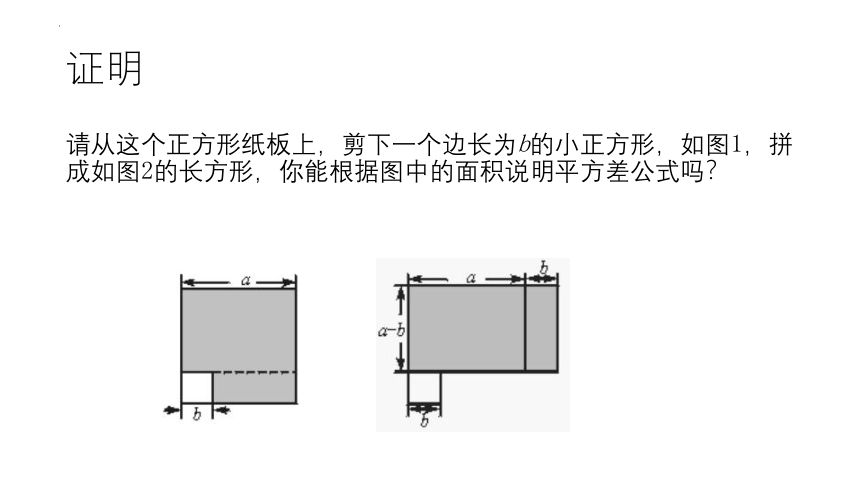
请从这个正方形纸板上,剪下一个边长为b的小正方形,如图1,拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?
例题
(3x+2 )( 3x-2 )
(b+2a)(2a-b).
练习
102×98.
(y+2)(y-2)-(y -1)(y+5).
探索
(a+b-c)(a-b-c)能用平方差公式运算吗
若能结果是哪两数的平方差
完全平方公式
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
探究
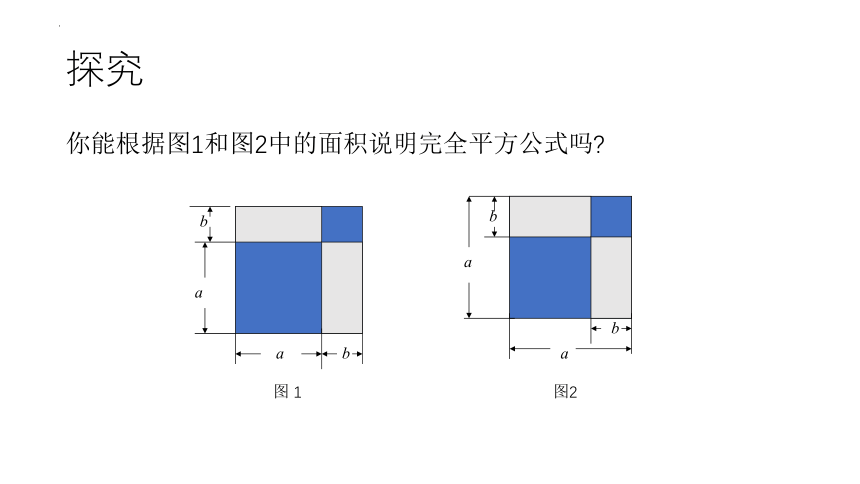
你能根据图1和图2中的面积说明完全平方公式吗
b
a
a
b
b
a
b
a
图 1
图2
例题
(4m+n)2
(x-2y)2
练习
1022
992
扩展----贾宪三角
中国的数学发展到宋元时期,终于走到了它的高峰。在这个数学创新的黄金时期中,各种数学成果层出不穷,令人目不暇接。其中特别引人注目的,当首推北宋数学家贾宪创制的“贾宪三角”了。
由于史书没有贾宪的传记,所以我们今天对这位数学家的生平事迹
已经无法搞清楚了。只知道他曾经当过宋代“左班殿直”的小官,是
当时天文数学家楚衍的学生,还写过两部数学著作,可惜这两部著
作现在都失传了。幸亏南宋数学家杨辉在他的书中引述了贾宪的许
多数学思想资料,才使我们今天得以了解贾宪在数学上的重大贡献。
贾宪最著名的数学成就,是他创制了
一幅数字图式,即“开方作法本源图” 。
这幅图现见于杨辉的书中,但杨辉在
引用了这幅图后特意说明:“贾宪用此
术”。所以过去我国数学界把这幅图称
为“杨辉三角”,实际上是不妥当的,
应该称为“贾宪三角”才最为恰当。
用现代的数学术语来说,这幅“开方作法本源图”实际上是一个指数为正整数的二项式定理系数表。稍懂代数的读者都知道:
如果把以上式子中等号右边的各个系数排列起来,则可得:
这正好与“开方作法本源图”上的数字完全相符。
这样一种二项式系数的展开规律,在西方数学史上被称为“帕斯卡三角形”。帕斯卡是法国数学家,他是在1654年所著的书中给出类似于贾宪“开方作法本源图”的数字三角形表的。其实在欧洲,类似的数字三角形也并非帕斯卡最先发明,只是开始没有广泛流传罢了。西方最古的此类数字三角形,可以上溯到1527年;但与贾宪的这个图相比,已经晚了四百多年。因此我们完全有理由把这项中国人最先发明的数学成果称为“贾宪三角”而载人史册。
不仅如此,贾宪的这个图还蕴含了图中数字的产生规律。细心的读者也许已经发现,这个三角形的两条斜边都是由数字1所组成的,而其他的数都等于它肩上的两个数相加。按此规律,这个数字三角形可以写到任意多层;也就是说,二项式任意正整次幂的
系数展开都可以按照这个图很容易地得到。
根据杨辉的记载,贾宪求“开方作法本源图”中各项系数的方法,就是他在开平方、开立方中所用的新法——“增乘开方法”。应用这种“增乘开方法”,既可求得任意高次展开式系数,又可进行任意高次幂的开方。在贾宪之前,从汉代一直到唐代的一千多年时间里,中国古代数学家只能进行正数的开平方和开立方运算,对于四次方以上的高次幂开方没有什么好的方法。直到贾宪的“增乘开方法”问世,才真正找到了开高次方的最佳方法,并能用它开任意有理数的高次方。这在中国数学史乃至世界数学史上,都是具有极其重要的价值的。以后的数学家在这个基础上继续前进,又把它推广为任意高次方程的数值解法。南宋时期的数学家秦九韶在系统总结前人成果的基础上,终于把以增乘开方法为主体的高次方程数值解法发展到了十分完备的程度。在秦九韶的著作中,方程的系数既有正的,也有负的;既有整数,也有小数;方程的次数最高达10次方。
其解法与现代通常使用的“霍纳法”(由英国数学家霍纳于1819年给出)基本一致,但比霍纳法要早了五百多年。从贾宪到秦九韶逐步发展完备起来的高次方程数值解法,是中国数学在宋元时期的一项杰出的创造。
小结
1. 计算(x-y)(-y-x)的结果是( )
A.-x2+y2 B. -x2-y2 C. x2-y2 D. x2+y2
2. 计算(x+3y)2-(3x+y)2的结果是( )
A. 8x2-8y2 B. 8y2-8x2
C. 8(x+y)2 D. 8(x-y)2
3. 若x2-y2=100, x+y= -25,则x-y的值是( )
A.5 B. 4 C. -4 D. 以上都不对
4. 若x-y=2,x2-y2=6,则x+y=________
5. 用简便方法计算:
503×497=_______;1.02×0.98=______
6. 计算:
(1)(3a-2b)(9a+6b)
(2)(2y-1)(4y2+1)(2y+1)
7. 已知a2-b2=8,a+b=4,求a、b的值
8. 下列计算正确的是( )
A.( 2a+b)( 2a b) = 2a2 b2
B.(0.3x+0.2)(0.3x 0.2) = 0.9x2 0.4
C.(a2+3b3)(3b3 a2) = a4 9b6
D.( 3a bc)( bc 3a) = 9a2+b 2c2
9. 下列各式中,不能用平方差公式计算的是( )
A.( 2b 5)(2b 5)
B.(b2+2x2)(2x2 b2)
C.( 1 4a)(1 4a)
D.( m2n+2)(m2n 2)
10. 若x2-y2=100, x+y= -25,则x-y的值是( )
A.5 B. 4 C. -4 D. 以上都不对
11. 化简(m2+1)(m+1)(m-1) -(m4+1)的值是( )
A. -2m2 B. 0 C.-2 D.-1
12. 如图所示,长方形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,求长方形ABCD中最大正方形与最小正方形的面积之差.
13. 已知x+y=6,xy=4,求①x2+y2,②(x-y)2,③x2+xy+y2的值.
14. [2x2-(x+y)(x-y)][(z-x)(x+z)+(y-z)(y+z)];
15. 已知△ABC的三边a、b、c满足a2+b2+c2-ab-bc-ac=0,试判断△ABC的形状.
16. 利用乘法公式进行简便运算:
①20042;
②999.82;
③(2+1)(22+1)(24+1)(28+1)(216+1)+1
14.2 乘法公式
复习
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn.
活动
1. (x+1)(x-1); 2. (a+2)(a-2);
3. (3-x)(3+x) ; 4. (2x+1)(2x-1).
观察上述算式,你能发现什么规律?运算出结果后,你又发现什么规律?
平方差公式
(a+b)(a- b)=a2- ab+ab- b2= a2- b2.
即两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式的逆用: a2-b2 = (a+b)(a-b)
证明
请从这个正方形纸板上,剪下一个边长为b的小正方形,如图1,拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?
例题
(3x+2 )( 3x-2 )
(b+2a)(2a-b).
练习
102×98.
(y+2)(y-2)-(y -1)(y+5).
探索
(a+b-c)(a-b-c)能用平方差公式运算吗
若能结果是哪两数的平方差
完全平方公式
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
探究
你能根据图1和图2中的面积说明完全平方公式吗
b
a
a
b
b
a
b
a
图 1
图2
例题
(4m+n)2
(x-2y)2
练习
1022
992
扩展----贾宪三角
中国的数学发展到宋元时期,终于走到了它的高峰。在这个数学创新的黄金时期中,各种数学成果层出不穷,令人目不暇接。其中特别引人注目的,当首推北宋数学家贾宪创制的“贾宪三角”了。
由于史书没有贾宪的传记,所以我们今天对这位数学家的生平事迹
已经无法搞清楚了。只知道他曾经当过宋代“左班殿直”的小官,是
当时天文数学家楚衍的学生,还写过两部数学著作,可惜这两部著
作现在都失传了。幸亏南宋数学家杨辉在他的书中引述了贾宪的许
多数学思想资料,才使我们今天得以了解贾宪在数学上的重大贡献。
贾宪最著名的数学成就,是他创制了
一幅数字图式,即“开方作法本源图” 。
这幅图现见于杨辉的书中,但杨辉在
引用了这幅图后特意说明:“贾宪用此
术”。所以过去我国数学界把这幅图称
为“杨辉三角”,实际上是不妥当的,
应该称为“贾宪三角”才最为恰当。
用现代的数学术语来说,这幅“开方作法本源图”实际上是一个指数为正整数的二项式定理系数表。稍懂代数的读者都知道:
如果把以上式子中等号右边的各个系数排列起来,则可得:
这正好与“开方作法本源图”上的数字完全相符。
这样一种二项式系数的展开规律,在西方数学史上被称为“帕斯卡三角形”。帕斯卡是法国数学家,他是在1654年所著的书中给出类似于贾宪“开方作法本源图”的数字三角形表的。其实在欧洲,类似的数字三角形也并非帕斯卡最先发明,只是开始没有广泛流传罢了。西方最古的此类数字三角形,可以上溯到1527年;但与贾宪的这个图相比,已经晚了四百多年。因此我们完全有理由把这项中国人最先发明的数学成果称为“贾宪三角”而载人史册。
不仅如此,贾宪的这个图还蕴含了图中数字的产生规律。细心的读者也许已经发现,这个三角形的两条斜边都是由数字1所组成的,而其他的数都等于它肩上的两个数相加。按此规律,这个数字三角形可以写到任意多层;也就是说,二项式任意正整次幂的
系数展开都可以按照这个图很容易地得到。
根据杨辉的记载,贾宪求“开方作法本源图”中各项系数的方法,就是他在开平方、开立方中所用的新法——“增乘开方法”。应用这种“增乘开方法”,既可求得任意高次展开式系数,又可进行任意高次幂的开方。在贾宪之前,从汉代一直到唐代的一千多年时间里,中国古代数学家只能进行正数的开平方和开立方运算,对于四次方以上的高次幂开方没有什么好的方法。直到贾宪的“增乘开方法”问世,才真正找到了开高次方的最佳方法,并能用它开任意有理数的高次方。这在中国数学史乃至世界数学史上,都是具有极其重要的价值的。以后的数学家在这个基础上继续前进,又把它推广为任意高次方程的数值解法。南宋时期的数学家秦九韶在系统总结前人成果的基础上,终于把以增乘开方法为主体的高次方程数值解法发展到了十分完备的程度。在秦九韶的著作中,方程的系数既有正的,也有负的;既有整数,也有小数;方程的次数最高达10次方。
其解法与现代通常使用的“霍纳法”(由英国数学家霍纳于1819年给出)基本一致,但比霍纳法要早了五百多年。从贾宪到秦九韶逐步发展完备起来的高次方程数值解法,是中国数学在宋元时期的一项杰出的创造。
小结
1. 计算(x-y)(-y-x)的结果是( )
A.-x2+y2 B. -x2-y2 C. x2-y2 D. x2+y2
2. 计算(x+3y)2-(3x+y)2的结果是( )
A. 8x2-8y2 B. 8y2-8x2
C. 8(x+y)2 D. 8(x-y)2
3. 若x2-y2=100, x+y= -25,则x-y的值是( )
A.5 B. 4 C. -4 D. 以上都不对
4. 若x-y=2,x2-y2=6,则x+y=________
5. 用简便方法计算:
503×497=_______;1.02×0.98=______
6. 计算:
(1)(3a-2b)(9a+6b)
(2)(2y-1)(4y2+1)(2y+1)
7. 已知a2-b2=8,a+b=4,求a、b的值
8. 下列计算正确的是( )
A.( 2a+b)( 2a b) = 2a2 b2
B.(0.3x+0.2)(0.3x 0.2) = 0.9x2 0.4
C.(a2+3b3)(3b3 a2) = a4 9b6
D.( 3a bc)( bc 3a) = 9a2+b 2c2
9. 下列各式中,不能用平方差公式计算的是( )
A.( 2b 5)(2b 5)
B.(b2+2x2)(2x2 b2)
C.( 1 4a)(1 4a)
D.( m2n+2)(m2n 2)
10. 若x2-y2=100, x+y= -25,则x-y的值是( )
A.5 B. 4 C. -4 D. 以上都不对
11. 化简(m2+1)(m+1)(m-1) -(m4+1)的值是( )
A. -2m2 B. 0 C.-2 D.-1
12. 如图所示,长方形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,求长方形ABCD中最大正方形与最小正方形的面积之差.
13. 已知x+y=6,xy=4,求①x2+y2,②(x-y)2,③x2+xy+y2的值.
14. [2x2-(x+y)(x-y)][(z-x)(x+z)+(y-z)(y+z)];
15. 已知△ABC的三边a、b、c满足a2+b2+c2-ab-bc-ac=0,试判断△ABC的形状.
16. 利用乘法公式进行简便运算:
①20042;
②999.82;
③(2+1)(22+1)(24+1)(28+1)(216+1)+1
