2021—2022学年沪科版数学七年级下册9.3.1分式方程 课件(共26张PPT)
文档属性
| 名称 | 2021—2022学年沪科版数学七年级下册9.3.1分式方程 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 16:52:12 | ||
图片预览






文档简介
(共26张PPT)
9. 3 分式方程
第1课时
学习目标
1.能够识别分式方程,了解解分式方程的整体思想及检验的意义;
2. 能够准确的求出分式方程的解;
3.在经历“实际问题-分式方程-整式方程”的过程,发展学生分析问题,解决问题的能力,渗透数学的转化思想,培养学生的应用意识;
4.在探究分式方程及其解法的过程中,培养学生的合作交流意识和探索精神,增进数学学习的信心,感受数学之美,探究之趣.
分式方程
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
2x+5=7;
9x–5;
(3) 6y+1>2y;
(4) 7–2=5;
(5) 4x+3y=3;
;
.
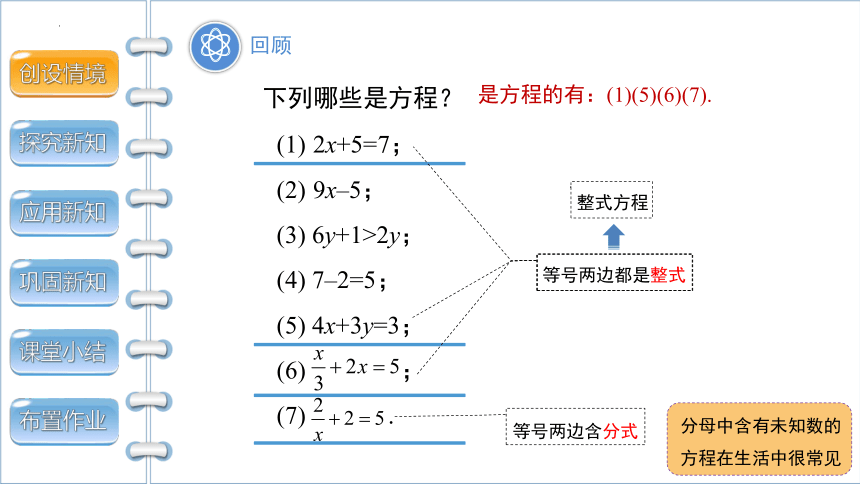
分母中含有未知数的方程在生活中很常见
下列哪些是方程?
是方程的有:(1)(5)(6)(7).
等号两边都是整式
整式方程
等号两边含分式
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
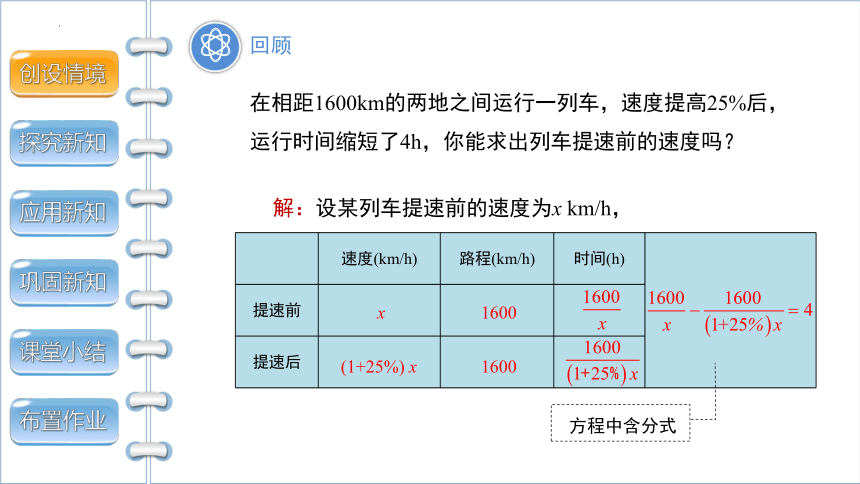
在相距1600km的两地之间运行一列车,速度提高25%后,运行时间缩短了4h,你能求出列车提速前的速度吗?
解:设某列车提速前的速度为x km/h,
速度(km/h) 路程(km/h) 时间(h)
提速前
提速后
x
(1+25%) x
1600
1600
方程中含分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
像这样,分母中含有未知数的方程叫做分式方程.
方程 , 的分母中含未知数x.
分式方程必须满足的条件(三者缺一不可)
(1) 是方程(含有未知数的等式);
(2) 含有分母;
(3) 分母中含有未知数.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
下列式子,哪些是分式方程?
①
②
③
④
⑤
π不是未知量,即分母没有未知数.
没有等号,不是方程.
判断是否为分式方程,看原式,不化简.
分母没有未知数.
② ④.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分式方程 整式方程
区别 分母中含有_______ 分母中___________
归纳
未知数
不含未知数
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
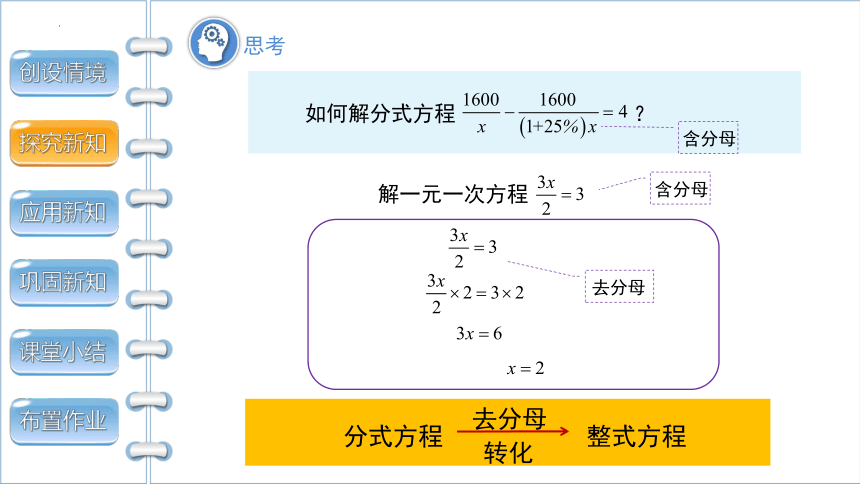
如何解分式方程 ?
俩人一组
合作讨论
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如何解分式方程 ?
解一元一次方程
去分母
含分母
含分母
去分母
分式方程
整式方程
转化
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
2000 – 1600= 5x.
整式方程
x=80.
把x=80代入上述分式方程检验:
左边 = =右边,
所以x= 80是该分式方程的根.
如何解分式方程 ?
解:
可转化为
方程两边同乘以最简公分母 ,得
解这个整式方程,得
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
解分式方程的基本思路:将分式方程化为整式方程.
具体做法:是“去分母”,即方程两边乘以最简公分母.这也是解分式方程的一般方法.
去分母
分式方程
整式方程
转化
方程两边同乘以最简公分母 x –3,得
解:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
如何解分式方程 ?把解得的根代入原方程中检验,你发现了什么?
探究
2–x= –1–2(x–3).
整式方程
把x=3代入上述分式方程检验:
所以x=3不是原方程的根,原方程无解.
x=3.
解这个整式方程,得
方程中分式的分母为零,
分式无意义,
像x=3这样的根,称为增根.
分式方程
必须验根
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
为什么 去分母后所得整式方程的解就是原分式方程的解,而 去分母后所得整式方程的解却不是原分式方程的解呢?
2000 – 1600= 5x
代入
x= 80
假设成立
等号两边同乘 (x – 3)
假设: x – 3 ≠0
2–x= –1–2(x–3)
代入
x= 3
x –3 =0
假设不成立
(是原方程的根)
(不是原方程的根)
等号两边同乘
假设:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
将整式方程的根代入最简公分母,如果最简公分母的值不为0,则整式方程的根是原分式方程的根;否则,这个根不是原分式方程的根.
一般地,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为0,因此应做如下检验:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
解分式方程的一般思想如下:
分式方程
去分母
整式方程
解整式方程
x=a
检验
最简公分母为0
a不是分式方程的根
a是分式方程的根
最简公分母不为0
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
解方程:
解:方程两边同乘以最简公分母(x + 3) (x – 3),得
(x – 1) (x – 3) –2(x + 3) (x – 3) = – x(x + 3).
展开得
x2 – 4x+3 – 2x2+18 = – x2– 3x.
检验:当x=21时,(x + 3) (x – 3)
因而,原方程的根是x=21.
≠0.
去分母
解整式方程
检验
写原分式方程的根
解方程,得
x = 21.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
交流
由以上解方程的过程,你能总结出解分式方程的步骤吗?
合作讨论
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
解分式方程的一般步骤
一去
二解
三验
四写
去分母,方程两边同乘最简公分母,把分式方程转化为整式方程.
解这个整式方程.
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的根是原分式方程的解;否则,这个根不是原分式方程的根.
写出原分式方程的根.
归纳
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
解方程:
解:方程两边同乘以最简公分母(x – 1) (x + 2),得
x(x + 2) – (x – 1) (x + 2) =3.
解得
x=1.
检验:当x=1时,(x – 1) (x + 2)
所以,原分式方程无根.
=0.
因而x=1不是原分式方程的根.
在去分母时,分式方程两边的每一项都要乘最简公分母,注意不要漏乘不含分母的项.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
下列方程是分式方程的是( )
A. B.
C. D. 2x+1=3x
B
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
解方程:
解:方程两边同乘以最简公分母x(x – 2),得
5(x – 2) =3x.
解得
x=5.
检验:当x=5时,x(x – 2)
≠0.
因此x=5是原分式方程的根.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
解方程:
解:方程两边同乘以最简公分母(x – 4) ,得
(x – 4) – 1 =3 – x.
解得
=0.
检验:当 时, x – 4
因此 不是原分式方程的根.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习4
随堂练习
解方程:
解:方程两边乘各分母的最简公分母x (x – 1)(x + 1),得
5(x – 1) – (x + 1) =0.
解得
≠0.
检验:当 时,2x(x + 2)
因此 是原分式方程的根.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式方程
分式方程必须满足的条件(三者缺一不可)
(1) 是方程(含有未知数的等式);
(2) 含有分母;
(3) 分母中含有未知数.
解分式方程的一般步骤
一去
二解
三验
四写
去分母,方程两边同乘最简公分母,把分式方程转化为整式方程.
解这个整式方程.
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的根是原分式方程的根;否则,这个根不是原分式方程的根.
写出原分式方程的根.
布置作业
教科书第109页习题3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
9. 3 分式方程
第1课时
学习目标
1.能够识别分式方程,了解解分式方程的整体思想及检验的意义;
2. 能够准确的求出分式方程的解;
3.在经历“实际问题-分式方程-整式方程”的过程,发展学生分析问题,解决问题的能力,渗透数学的转化思想,培养学生的应用意识;
4.在探究分式方程及其解法的过程中,培养学生的合作交流意识和探索精神,增进数学学习的信心,感受数学之美,探究之趣.
分式方程
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
2x+5=7;
9x–5;
(3) 6y+1>2y;
(4) 7–2=5;
(5) 4x+3y=3;
;
.
分母中含有未知数的方程在生活中很常见
下列哪些是方程?
是方程的有:(1)(5)(6)(7).
等号两边都是整式
整式方程
等号两边含分式
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
在相距1600km的两地之间运行一列车,速度提高25%后,运行时间缩短了4h,你能求出列车提速前的速度吗?
解:设某列车提速前的速度为x km/h,
速度(km/h) 路程(km/h) 时间(h)
提速前
提速后
x
(1+25%) x
1600
1600
方程中含分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
像这样,分母中含有未知数的方程叫做分式方程.
方程 , 的分母中含未知数x.
分式方程必须满足的条件(三者缺一不可)
(1) 是方程(含有未知数的等式);
(2) 含有分母;
(3) 分母中含有未知数.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
下列式子,哪些是分式方程?
①
②
③
④
⑤
π不是未知量,即分母没有未知数.
没有等号,不是方程.
判断是否为分式方程,看原式,不化简.
分母没有未知数.
② ④.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分式方程 整式方程
区别 分母中含有_______ 分母中___________
归纳
未知数
不含未知数
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如何解分式方程 ?
俩人一组
合作讨论
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如何解分式方程 ?
解一元一次方程
去分母
含分母
含分母
去分母
分式方程
整式方程
转化
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
2000 – 1600= 5x.
整式方程
x=80.
把x=80代入上述分式方程检验:
左边 = =右边,
所以x= 80是该分式方程的根.
如何解分式方程 ?
解:
可转化为
方程两边同乘以最简公分母 ,得
解这个整式方程,得
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
解分式方程的基本思路:将分式方程化为整式方程.
具体做法:是“去分母”,即方程两边乘以最简公分母.这也是解分式方程的一般方法.
去分母
分式方程
整式方程
转化
方程两边同乘以最简公分母 x –3,得
解:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
如何解分式方程 ?把解得的根代入原方程中检验,你发现了什么?
探究
2–x= –1–2(x–3).
整式方程
把x=3代入上述分式方程检验:
所以x=3不是原方程的根,原方程无解.
x=3.
解这个整式方程,得
方程中分式的分母为零,
分式无意义,
像x=3这样的根,称为增根.
分式方程
必须验根
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
为什么 去分母后所得整式方程的解就是原分式方程的解,而 去分母后所得整式方程的解却不是原分式方程的解呢?
2000 – 1600= 5x
代入
x= 80
假设成立
等号两边同乘 (x – 3)
假设: x – 3 ≠0
2–x= –1–2(x–3)
代入
x= 3
x –3 =0
假设不成立
(是原方程的根)
(不是原方程的根)
等号两边同乘
假设:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
将整式方程的根代入最简公分母,如果最简公分母的值不为0,则整式方程的根是原分式方程的根;否则,这个根不是原分式方程的根.
一般地,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为0,因此应做如下检验:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
解分式方程的一般思想如下:
分式方程
去分母
整式方程
解整式方程
x=a
检验
最简公分母为0
a不是分式方程的根
a是分式方程的根
最简公分母不为0
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
解方程:
解:方程两边同乘以最简公分母(x + 3) (x – 3),得
(x – 1) (x – 3) –2(x + 3) (x – 3) = – x(x + 3).
展开得
x2 – 4x+3 – 2x2+18 = – x2– 3x.
检验:当x=21时,(x + 3) (x – 3)
因而,原方程的根是x=21.
≠0.
去分母
解整式方程
检验
写原分式方程的根
解方程,得
x = 21.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
交流
由以上解方程的过程,你能总结出解分式方程的步骤吗?
合作讨论
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
解分式方程的一般步骤
一去
二解
三验
四写
去分母,方程两边同乘最简公分母,把分式方程转化为整式方程.
解这个整式方程.
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的根是原分式方程的解;否则,这个根不是原分式方程的根.
写出原分式方程的根.
归纳
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
解方程:
解:方程两边同乘以最简公分母(x – 1) (x + 2),得
x(x + 2) – (x – 1) (x + 2) =3.
解得
x=1.
检验:当x=1时,(x – 1) (x + 2)
所以,原分式方程无根.
=0.
因而x=1不是原分式方程的根.
在去分母时,分式方程两边的每一项都要乘最简公分母,注意不要漏乘不含分母的项.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
下列方程是分式方程的是( )
A. B.
C. D. 2x+1=3x
B
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
解方程:
解:方程两边同乘以最简公分母x(x – 2),得
5(x – 2) =3x.
解得
x=5.
检验:当x=5时,x(x – 2)
≠0.
因此x=5是原分式方程的根.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
解方程:
解:方程两边同乘以最简公分母(x – 4) ,得
(x – 4) – 1 =3 – x.
解得
=0.
检验:当 时, x – 4
因此 不是原分式方程的根.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习4
随堂练习
解方程:
解:方程两边乘各分母的最简公分母x (x – 1)(x + 1),得
5(x – 1) – (x + 1) =0.
解得
≠0.
检验:当 时,2x(x + 2)
因此 是原分式方程的根.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式方程
分式方程必须满足的条件(三者缺一不可)
(1) 是方程(含有未知数的等式);
(2) 含有分母;
(3) 分母中含有未知数.
解分式方程的一般步骤
一去
二解
三验
四写
去分母,方程两边同乘最简公分母,把分式方程转化为整式方程.
解这个整式方程.
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的根是原分式方程的根;否则,这个根不是原分式方程的根.
写出原分式方程的根.
布置作业
教科书第109页习题3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
