沪科版七年级下册9.1分式及其基本性质(第3课时)课件(共16张PPT)
文档属性
| 名称 | 沪科版七年级下册9.1分式及其基本性质(第3课时)课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
9.1 分式及其基本性质
第3课时 分式的约分
学习目标
1.了解分式约分的意义,理解最简分式的概念;
2.掌握分式约分的方法和步骤,能够熟练计算;
3.经历了从分数的约分到分式的约分的过程,培养学生观察、类比、推理的数学思维能力;
4. 通过研究解决问题的过程,培养学生合作交流意识与探究精神,形成勤奋学习的良好习惯.
分式的约分
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
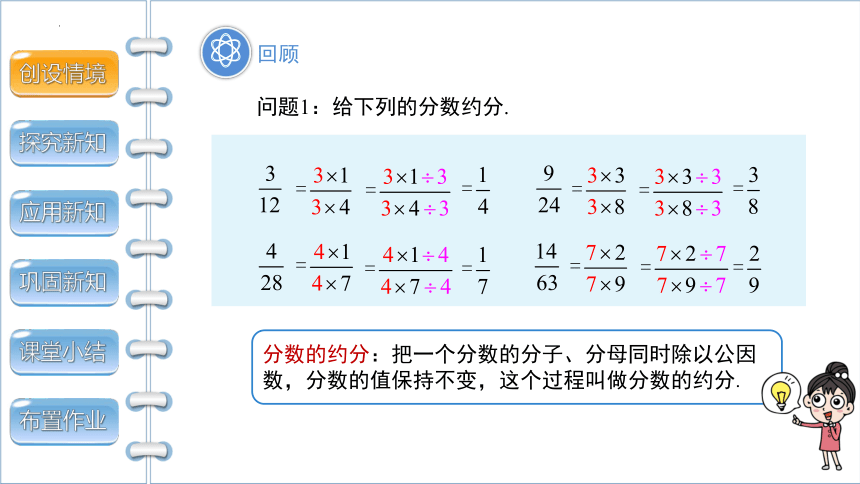
问题1:给下列的分数约分.
分数的约分:把一个分数的分子、分母同时除以公因数,分数的值保持不变,这个过程叫做分数的约分.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
问题2:根据分式的基本性质填空.
分母除以y
分子除以y
分母除以2x
分子除以2x
y2
2x
(1)
(2)
分式的基本性质:分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
联想分数的约分,根据分式的基本性质,你能想出如何对下列分式进行约分吗?
思考
俩人一组
合作完成
分子、分母的公因式为x.
分子、分母的公因式为3x.
最简分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
根据分式的基本性质,把一个分式的分子和分母的公因式约去叫做分式的约分.
分式的约分
例如:
分子与分母只有公因式1的分式,叫做最简分式.
不是最简分式
若分式的分子、分母都是单项式,就直接约去分子、分母的公因式,即分子、分母系数的最大公约数和分子、分母中的相同字母的最低次幂的乘积,使所得结果成为最简分式或者整式.
若分式的分子或分母含有多项式,应先分解因式,再确定公因式并约去.
使所得结果成为最简分式或者整式.
巩固新知
课堂小结
布置作业
创设情境
约分:
解:
约分前,要先找出分子和分母的公因式.
探究新知
应用新知
典型例题
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
(1)若分式的分子、分母都是单项式,就直接约去分子、分母的公因式,即分子、分母系数的最大公约数和分子、分母中的相同字母的最低次幂的乘积,使所得结果成为最简分式或者整式.
(2)若分式的分子或分母含有多项式,应先分解因式,再确定公因式并约去. 使所得结果成为最简分式或者整式.
分式的约分的一般方法
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
(1)约分的依据是分式的基本性质,约分的关键是确定分子和分母的公因式;
(2)约分是针对分式的分子和分母整体进行的,而不是针对其中的某些项,因此约分前一定要确认分子和分母都是乘积的形式;
(3)约分一定要彻底,即约分的结果必须是最简分式或整式.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
解:
约分:
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
解:
约分:
应用新知
课堂小结
布置作业
创设情境
练习3
探究新知
巩固新知
计算 的结果为( )
A. 1 B. C. D.0
A
解析:
随堂练习
应用新知
布置作业
创设情境
探究新知
巩固新知
练习4
课堂小结
先化简,再求值:
(1) ,其中x= –2,y=3.
,其中a= –4,b=2.
分析:分子、分母能分解因式的先分解因式,然后根据分式的基本性质约分,一定要化简成最简分式或整式,再将字母的值代入求解.
解:(1) .
当x= – 2,y=3时,原式= .
当a= – 4,b=2时,原式= – 5.
(2) .
随堂练习
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
根据分式的基本性质,把一个分式的分子和分母的公因式约去叫做分式的约分.
分式的约分
分子与分母只有公因式1的分式,叫做最简分式.
(1)约分的依据是分式的基本性质,约分的关键是确定分子和分母的公因式;
(2)约分是针对分式的分子和分母整体进行的,而不是针对其中的某些项,因此约分前一定要确认分子和分母都是乘积的形式;
(3)约分一定要彻底,即约分的结果必须是最简分式或整式.
约分的注意事项
分式的约分
布置作业
教科书第93页练习3;
第94页习题6、习题7.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
9.1 分式及其基本性质
第3课时 分式的约分
学习目标
1.了解分式约分的意义,理解最简分式的概念;
2.掌握分式约分的方法和步骤,能够熟练计算;
3.经历了从分数的约分到分式的约分的过程,培养学生观察、类比、推理的数学思维能力;
4. 通过研究解决问题的过程,培养学生合作交流意识与探究精神,形成勤奋学习的良好习惯.
分式的约分
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
问题1:给下列的分数约分.
分数的约分:把一个分数的分子、分母同时除以公因数,分数的值保持不变,这个过程叫做分数的约分.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
问题2:根据分式的基本性质填空.
分母除以y
分子除以y
分母除以2x
分子除以2x
y2
2x
(1)
(2)
分式的基本性质:分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
联想分数的约分,根据分式的基本性质,你能想出如何对下列分式进行约分吗?
思考
俩人一组
合作完成
分子、分母的公因式为x.
分子、分母的公因式为3x.
最简分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
根据分式的基本性质,把一个分式的分子和分母的公因式约去叫做分式的约分.
分式的约分
例如:
分子与分母只有公因式1的分式,叫做最简分式.
不是最简分式
若分式的分子、分母都是单项式,就直接约去分子、分母的公因式,即分子、分母系数的最大公约数和分子、分母中的相同字母的最低次幂的乘积,使所得结果成为最简分式或者整式.
若分式的分子或分母含有多项式,应先分解因式,再确定公因式并约去.
使所得结果成为最简分式或者整式.
巩固新知
课堂小结
布置作业
创设情境
约分:
解:
约分前,要先找出分子和分母的公因式.
探究新知
应用新知
典型例题
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
(1)若分式的分子、分母都是单项式,就直接约去分子、分母的公因式,即分子、分母系数的最大公约数和分子、分母中的相同字母的最低次幂的乘积,使所得结果成为最简分式或者整式.
(2)若分式的分子或分母含有多项式,应先分解因式,再确定公因式并约去. 使所得结果成为最简分式或者整式.
分式的约分的一般方法
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
(1)约分的依据是分式的基本性质,约分的关键是确定分子和分母的公因式;
(2)约分是针对分式的分子和分母整体进行的,而不是针对其中的某些项,因此约分前一定要确认分子和分母都是乘积的形式;
(3)约分一定要彻底,即约分的结果必须是最简分式或整式.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
解:
约分:
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
解:
约分:
应用新知
课堂小结
布置作业
创设情境
练习3
探究新知
巩固新知
计算 的结果为( )
A. 1 B. C. D.0
A
解析:
随堂练习
应用新知
布置作业
创设情境
探究新知
巩固新知
练习4
课堂小结
先化简,再求值:
(1) ,其中x= –2,y=3.
,其中a= –4,b=2.
分析:分子、分母能分解因式的先分解因式,然后根据分式的基本性质约分,一定要化简成最简分式或整式,再将字母的值代入求解.
解:(1) .
当x= – 2,y=3时,原式= .
当a= – 4,b=2时,原式= – 5.
(2) .
随堂练习
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
根据分式的基本性质,把一个分式的分子和分母的公因式约去叫做分式的约分.
分式的约分
分子与分母只有公因式1的分式,叫做最简分式.
(1)约分的依据是分式的基本性质,约分的关键是确定分子和分母的公因式;
(2)约分是针对分式的分子和分母整体进行的,而不是针对其中的某些项,因此约分前一定要确认分子和分母都是乘积的形式;
(3)约分一定要彻底,即约分的结果必须是最简分式或整式.
约分的注意事项
分式的约分
布置作业
教科书第93页练习3;
第94页习题6、习题7.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
