2021—2022学年沪科版数学七年级下册9.1分式及其基本性质第1课时 课件(共24张PPT)
文档属性
| 名称 | 2021—2022学年沪科版数学七年级下册9.1分式及其基本性质第1课时 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 19:38:26 | ||
图片预览








文档简介
(共24张PPT)
9.1 分式及其基本性质
第1课时 分式的概念
学习目标
1.了解分式的概念,能识别分式;能用分式表示数量关系.
2.会判断分式中的字母满足什么条件时分式有意义,分式值为零.
3.经历从分数到分式概念的形成过程,体会从特殊到一般、从一般到特殊的数学思想方法;通过从具体情境中抽象出数量关系和变化规律,培养学生的符号感.
4.感悟数学在实际生活中的应用,增强数学应用意识,认识到数学的学习价值,激发学习数学的兴趣.
分式的概念
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题1:下列各式哪些是整式?
回顾
整式
单个数、单个字母、数与字母的积,字母与字母的积.
几个单项式的和.
单项式
多项式
整式:
不是整式,那么它们是什么呢?
应用新知
巩固新知
课堂小结
布置作业
5÷3=________, 2 ÷ 3=________.
问题3:试用类似分数的形式表示下列两个整式相除:
(1) 90÷x 可以用式子 来表示.
(2) (x+3) ÷(x–6)可以用式子 来表示.
问题2:将下列两个整数相除表示成分数的形式:
创设情境
探究新知
两个整式相除也可以有类似地表示.
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题① 有两块稻田,第一块是4 hm2,每公顷收水稻10500kg;第二块是3hm2,每公顷收水稻9000kg ,这两块稻田平均每公顷收水稻_______________kg.
如果第一块是m hm2 ,每公顷收水稻a kg;第二块是n hm2 ,每公顷收水稻b kg ,则这两块稻田平均每公顷收水稻____kg.
问题② 一个长方形的面积为s m2 ,如果它的长为a m,那么它的宽为_____m.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
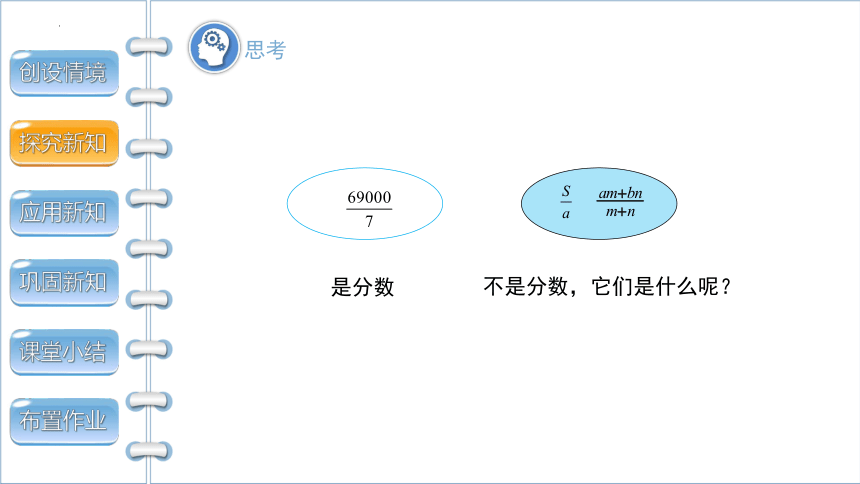
思考
是分数
不是分数,它们是什么呢?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
式子 有什么共同特征?与整式有什么不同?
思考
3. 它们是整式吗?
1. 它们与分数有什么相同点?
2. 它们与分数有什么不同点?
都不是整式(整式的分母不含字母).
与分数的形式相同,
都是 的形式.
整式.
整式.
(都含有字母).
提示
分数的分母为数,它们的分母含字母
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
式子 有什么共同特征?与整式有什么不同?
思考
1.它们的共同特征是分母中都含有字母.
2. 与整式不同,整式中分母不含有字母.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
一般地,如果a,b表示两个整式,并且b中含有字母,那么式子 叫做分式.其中a叫做分式的分子,b叫做分式分母.
整式和分式统称为有理式.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
1. 分式是不同于整式的另一类式子,两类式子的区别是分母是否含有字母.
2. 分式的分子a可以含有字母,也可以不含字母,分母b中必须含有字母.
3. 由于字母可以表示不同的数,所以分式比分数更具有一般性.
仅表示2÷3的商,而分式 既可以表示2÷3,又可表示(– 5)÷2,8÷(– 9)等.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
下列式子中,哪些是分式?哪些是整式?
1. 判断时,注意含有π的式子,π是常数,不是字母.
整式
2. 式子中含有多项时,若其中有一项分母含有字母,则该式也为分式(如 ).
整式
整式
整式
分式
分式
分式
分式
整式
分式
分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
提示
1. 分数 有意义吗?
没有意义
分数有意义的条件是分母不为0.
2. 类似地分式 有意义的条件是什么呢?
分式有意义的条件是分母b≠0.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
分式 中,
当分母b=0时, 分式 无意义.
当分母b≠0时,分式 有意义.
(与分子a无关)
练习:当x取何值时,分式 有意义?
要使分式 有意义,则分母x –2≠0,即x ≠2.
当分母的值等于零时,分式没有意义,除此以外,分式都有意义.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
提示
= ( )
在什么条件下,分式 的值为0?
= ( )
时,即a=0
,且b≠0时.
0
0
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
当 =0时,
a=0且b≠0
当x是什么数时,分式 的值是零?
要使分式 的值是零 ,则分子x+4= 0且分母2x –3≠0.
x+4= 0,即x= – 4.
2x –3≠0,即
综上所述,x= – 4时,分式 的值为零.
巩固新知
课堂小结
布置作业
创设情境
下列分式中的字母满足什么条件时分式有意义?
探究新知
应用新知
典型例题
(1)
(2)
(3)
(4)
解:(1)要使分式 有意义,
(2)要使分式 有意义,
(3)要使分式 有意义,
(4)要使分式 有意义,
则分母3x≠0,即x ≠ 0;
则分母x–1≠0,即x ≠ 1;
则分母5–3b≠0,即b ≠ ;
则分母x–y≠0,即x ≠ y.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
下列有理式中: 其中分式共有( )
A. 1个 B. 2个 C. 3个 D. 4个
B
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
x为何值时,分式 无意义( )
A. x=3
B. x=–3
C. x=–2
D. x是不等于3的任何数
A
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
已知分式 ,
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
(3) 当x为何值时,分式的值为零
(2) 分式有意义,即分母 x+2≠0,得 x ≠ –2.
解:
(1) 分式无意义,即分母 x+2=0,得 x= –2.
(3) 分式的值为零,即分母 x+2 ≠0 且分子x2–4=0,
由x+2≠0,可知 x≠–2,
即当x= –2时,分式 无意义.
由x2–4=0,得 x=±2,
综上所述: x=2.
即当x ≠–2时,分式 有意义.
即当x =2时,分式 的值为零.
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习4
无论x为何值,下列分式一定有意义的是( )
A. B. C. D.
D
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习5
在分式 中,如果x= –a,则下列结论中正确的是( )
不论a为何值,分式都无意义.
不论a为何值,分式的值均为零.
若a≠ ,则分式的值是零.
若a≠ ,则分式的值是零.
D
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
一般地,如果a,b表示两个整式,并且b中含有字母,那么式子 叫做分式.a叫做分子,b叫做分母.
分式 中,
当分母b=0时, 分式 无意义.
当分母b≠0时,分式 有意义.
(与分子a无关)
当a=0且b≠0时,分式 的值为零.
分式的概念
布置作业
教科书第90页,习题3.
93页,习题1、2.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
9.1 分式及其基本性质
第1课时 分式的概念
学习目标
1.了解分式的概念,能识别分式;能用分式表示数量关系.
2.会判断分式中的字母满足什么条件时分式有意义,分式值为零.
3.经历从分数到分式概念的形成过程,体会从特殊到一般、从一般到特殊的数学思想方法;通过从具体情境中抽象出数量关系和变化规律,培养学生的符号感.
4.感悟数学在实际生活中的应用,增强数学应用意识,认识到数学的学习价值,激发学习数学的兴趣.
分式的概念
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题1:下列各式哪些是整式?
回顾
整式
单个数、单个字母、数与字母的积,字母与字母的积.
几个单项式的和.
单项式
多项式
整式:
不是整式,那么它们是什么呢?
应用新知
巩固新知
课堂小结
布置作业
5÷3=________, 2 ÷ 3=________.
问题3:试用类似分数的形式表示下列两个整式相除:
(1) 90÷x 可以用式子 来表示.
(2) (x+3) ÷(x–6)可以用式子 来表示.
问题2:将下列两个整数相除表示成分数的形式:
创设情境
探究新知
两个整式相除也可以有类似地表示.
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题① 有两块稻田,第一块是4 hm2,每公顷收水稻10500kg;第二块是3hm2,每公顷收水稻9000kg ,这两块稻田平均每公顷收水稻_______________kg.
如果第一块是m hm2 ,每公顷收水稻a kg;第二块是n hm2 ,每公顷收水稻b kg ,则这两块稻田平均每公顷收水稻____kg.
问题② 一个长方形的面积为s m2 ,如果它的长为a m,那么它的宽为_____m.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
是分数
不是分数,它们是什么呢?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
式子 有什么共同特征?与整式有什么不同?
思考
3. 它们是整式吗?
1. 它们与分数有什么相同点?
2. 它们与分数有什么不同点?
都不是整式(整式的分母不含字母).
与分数的形式相同,
都是 的形式.
整式.
整式.
(都含有字母).
提示
分数的分母为数,它们的分母含字母
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
式子 有什么共同特征?与整式有什么不同?
思考
1.它们的共同特征是分母中都含有字母.
2. 与整式不同,整式中分母不含有字母.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
一般地,如果a,b表示两个整式,并且b中含有字母,那么式子 叫做分式.其中a叫做分式的分子,b叫做分式分母.
整式和分式统称为有理式.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
1. 分式是不同于整式的另一类式子,两类式子的区别是分母是否含有字母.
2. 分式的分子a可以含有字母,也可以不含字母,分母b中必须含有字母.
3. 由于字母可以表示不同的数,所以分式比分数更具有一般性.
仅表示2÷3的商,而分式 既可以表示2÷3,又可表示(– 5)÷2,8÷(– 9)等.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
下列式子中,哪些是分式?哪些是整式?
1. 判断时,注意含有π的式子,π是常数,不是字母.
整式
2. 式子中含有多项时,若其中有一项分母含有字母,则该式也为分式(如 ).
整式
整式
整式
分式
分式
分式
分式
整式
分式
分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
提示
1. 分数 有意义吗?
没有意义
分数有意义的条件是分母不为0.
2. 类似地分式 有意义的条件是什么呢?
分式有意义的条件是分母b≠0.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
分式 中,
当分母b=0时, 分式 无意义.
当分母b≠0时,分式 有意义.
(与分子a无关)
练习:当x取何值时,分式 有意义?
要使分式 有意义,则分母x –2≠0,即x ≠2.
当分母的值等于零时,分式没有意义,除此以外,分式都有意义.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
提示
= ( )
在什么条件下,分式 的值为0?
= ( )
时,即a=0
,且b≠0时.
0
0
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
当 =0时,
a=0且b≠0
当x是什么数时,分式 的值是零?
要使分式 的值是零 ,则分子x+4= 0且分母2x –3≠0.
x+4= 0,即x= – 4.
2x –3≠0,即
综上所述,x= – 4时,分式 的值为零.
巩固新知
课堂小结
布置作业
创设情境
下列分式中的字母满足什么条件时分式有意义?
探究新知
应用新知
典型例题
(1)
(2)
(3)
(4)
解:(1)要使分式 有意义,
(2)要使分式 有意义,
(3)要使分式 有意义,
(4)要使分式 有意义,
则分母3x≠0,即x ≠ 0;
则分母x–1≠0,即x ≠ 1;
则分母5–3b≠0,即b ≠ ;
则分母x–y≠0,即x ≠ y.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
下列有理式中: 其中分式共有( )
A. 1个 B. 2个 C. 3个 D. 4个
B
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
x为何值时,分式 无意义( )
A. x=3
B. x=–3
C. x=–2
D. x是不等于3的任何数
A
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
已知分式 ,
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
(3) 当x为何值时,分式的值为零
(2) 分式有意义,即分母 x+2≠0,得 x ≠ –2.
解:
(1) 分式无意义,即分母 x+2=0,得 x= –2.
(3) 分式的值为零,即分母 x+2 ≠0 且分子x2–4=0,
由x+2≠0,可知 x≠–2,
即当x= –2时,分式 无意义.
由x2–4=0,得 x=±2,
综上所述: x=2.
即当x ≠–2时,分式 有意义.
即当x =2时,分式 的值为零.
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习4
无论x为何值,下列分式一定有意义的是( )
A. B. C. D.
D
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习5
在分式 中,如果x= –a,则下列结论中正确的是( )
不论a为何值,分式都无意义.
不论a为何值,分式的值均为零.
若a≠ ,则分式的值是零.
若a≠ ,则分式的值是零.
D
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
一般地,如果a,b表示两个整式,并且b中含有字母,那么式子 叫做分式.a叫做分子,b叫做分母.
分式 中,
当分母b=0时, 分式 无意义.
当分母b≠0时,分式 有意义.
(与分子a无关)
当a=0且b≠0时,分式 的值为零.
分式的概念
布置作业
教科书第90页,习题3.
93页,习题1、2.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
