13.2.3 全等三角形-边角边 课件(23张ppt)
文档属性
| 名称 | 13.2.3 全等三角形-边角边 课件(23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-01 21:14:37 | ||
图片预览







文档简介
(共23张PPT)
13.2.3 全等三角形-边角边
华师大版 八年级上册
教学目标
1.掌握全等三角形的判定(S.A.S.),会进行全等的简单推理.
2.会用S.A.S.证明两个三角形全等.
3.应用综合法的格式证明三角形全等.
新知导入
问题:因铺设电线的需要,要在池塘两侧 A 、B 处各埋设一根电线杆(如图),现有一足够长的米尺却无法直接量出 A 、B 两点间的距离.
同学们,你们知道怎样测出A 、B 两点之间的距离吗?
新知讲解
探索
为了探索三角形全等的条件,现在我们考虑两个三角形有三组对应相等的元素,那么此时会出现几种可能的情况呢?
将六个元素(三条边、三个角)分类组合,可能出现:
两边一角对应相等,
两角一边对应相等,
三角对应相等,
三边对应相等.
你认为这些情况下,两个三角形会全等吗?
新知讲解
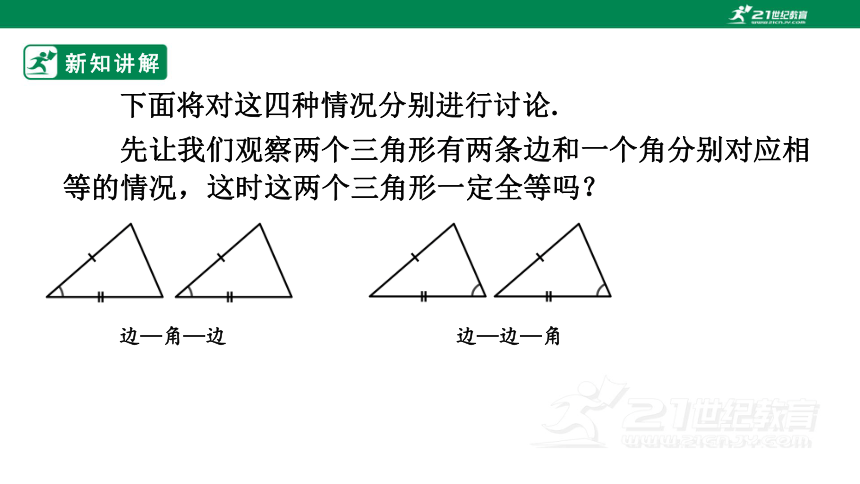
下面将对这四种情况分别进行讨论.
先让我们观察两个三角形有两条边和一个角分别对应相等的情况,这时这两个三角形一定全等吗?
边—角—边
边—边—角
新知讲解
如图,已知两条线段和一个角,试画一个三角形,使这两条线段为其两边,这个角为这两边的夹角.
把你画的三角形与其他同学画的三角形进行比较,看看是否完全重合.
新知讲解
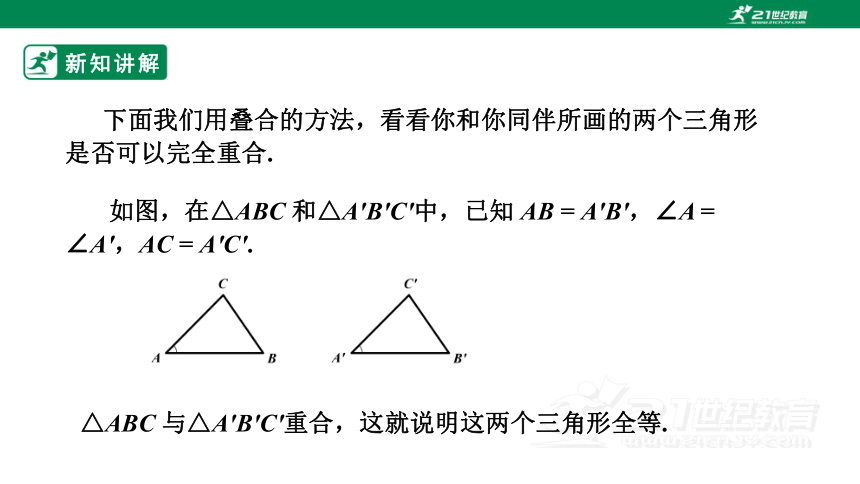
下面我们用叠合的方法,看看你和你同伴所画的两个三角形是否可以完全重合.
如图,在△ABC 和△A′B′C′中,已知 AB = A′B′,∠A = ∠A′,AC = A'C'.
△ABC 与△A′B′C′重合,这就说明这两个三角形全等.
新知讲解
由此可得判定三角形全等的一种简便方法:
基本事实 两边及其夹角分别相等的两个三角形全等.
简记为 S.A.S(或边角边)
“边角边”判定定理用符号语言表示为:
例如:在△ABC和△A′B′C′中,
AB=A′B′,∠A=∠A′,AC=A′C′
则△ABC≌△A′B′C′(S.A.S.).
例题讲解
例1 如图,已知线段AC、BD相交于点E,AE=DE, BE=CE,求证:△ABE≌△DCE.
证明:在△ABE和△DCE中,
∵AE = DE(已知),
∠AEB = ∠DEC (对顶角相等),
BE = CE(已知),
∴△ ABE≌DCE ( S.A.S.).
巩固练习
1.根据下面的条件,能否判断如图所示的两个三角形全等?
(1)AC = DF,∠C = ∠F,BC = EF;
(2)BC = BD,∠ABC =∠ABD.
(1)
(2)
能
能
巩固练习
证明: 在△ADC 和△AEB 中,
∵AD =AE,∠A =∠A ,AC=AB,
∴△ADC≌△AEB (S.A.S.).
2. 如图,在△ABC中,AB = AC,在 AB、AC 上分别截取相等的两条线段 AD、AE,并连结 BE、CD. 求证:△ADC ≌△AEB.
新知讲解
如图,已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形.
此时(即“边边角”对应相等) 两个三角形不一定全等.
A
B
C
D
典例讲解
例2 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA,连结BC并延长到E,使CE=CB.连结DE,那么DE的长就是A、B的距离。你知道其中的道理吗
典例讲解
例2已知:AD与BE相交点C,CA=CD,CB=CE.
求证: AB = DE.
证明:在△ACB和△DCE中,
∵CA=CD(已知),
∠1 =∠2 (对顶角相等),
CB=CE(已知),
∴△ACB≌△DCE(S.A.S. ).
∴AB = DE (全等三角形的对应边相等).
巩固练习
3. 如图所示,小明想设计一种测零件内径 AB 的卡钳.在卡钳的设计中,要使测出的 DC 长度恰好为内径 AB 的长度,那么卡钳各部分的尺寸应满足什么条件呢?请提出你的想法.
解: 满足 OA = OC,OB=OD .
∵OA = OC,OB=OD ,∠AOB=∠COD ,
∴△AOB≌△COD (S.A.S.),
∴AB=CD .
课堂总结
边角边
判定定理
两边及其夹角分别相等的两个三角形全等
应用边角边证明全等,解决问题
应用
拓展提高
1、如图AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向终点B运动,同时点Q在线段BD由点B向终点D运动,则当点Q的运动速度为________cm/s时,能够在某一时刻使△ACB与△BPQ全等。
1.5或1
拓展提高
拓展提高
2、如图,在△ABC中,BE、CF分别是ACAB两边上的高,且它们交于点H,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG.
(1)求证:AD=AG
(2)判断AD与AG的位置关系,请说明理由。
拓展提高
拓展提高
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.2.3 全等三角形-边角边
华师大版 八年级上册
教学目标
1.掌握全等三角形的判定(S.A.S.),会进行全等的简单推理.
2.会用S.A.S.证明两个三角形全等.
3.应用综合法的格式证明三角形全等.
新知导入
问题:因铺设电线的需要,要在池塘两侧 A 、B 处各埋设一根电线杆(如图),现有一足够长的米尺却无法直接量出 A 、B 两点间的距离.
同学们,你们知道怎样测出A 、B 两点之间的距离吗?
新知讲解
探索
为了探索三角形全等的条件,现在我们考虑两个三角形有三组对应相等的元素,那么此时会出现几种可能的情况呢?
将六个元素(三条边、三个角)分类组合,可能出现:
两边一角对应相等,
两角一边对应相等,
三角对应相等,
三边对应相等.
你认为这些情况下,两个三角形会全等吗?
新知讲解
下面将对这四种情况分别进行讨论.
先让我们观察两个三角形有两条边和一个角分别对应相等的情况,这时这两个三角形一定全等吗?
边—角—边
边—边—角
新知讲解
如图,已知两条线段和一个角,试画一个三角形,使这两条线段为其两边,这个角为这两边的夹角.
把你画的三角形与其他同学画的三角形进行比较,看看是否完全重合.
新知讲解
下面我们用叠合的方法,看看你和你同伴所画的两个三角形是否可以完全重合.
如图,在△ABC 和△A′B′C′中,已知 AB = A′B′,∠A = ∠A′,AC = A'C'.
△ABC 与△A′B′C′重合,这就说明这两个三角形全等.
新知讲解
由此可得判定三角形全等的一种简便方法:
基本事实 两边及其夹角分别相等的两个三角形全等.
简记为 S.A.S(或边角边)
“边角边”判定定理用符号语言表示为:
例如:在△ABC和△A′B′C′中,
AB=A′B′,∠A=∠A′,AC=A′C′
则△ABC≌△A′B′C′(S.A.S.).
例题讲解
例1 如图,已知线段AC、BD相交于点E,AE=DE, BE=CE,求证:△ABE≌△DCE.
证明:在△ABE和△DCE中,
∵AE = DE(已知),
∠AEB = ∠DEC (对顶角相等),
BE = CE(已知),
∴△ ABE≌DCE ( S.A.S.).
巩固练习
1.根据下面的条件,能否判断如图所示的两个三角形全等?
(1)AC = DF,∠C = ∠F,BC = EF;
(2)BC = BD,∠ABC =∠ABD.
(1)
(2)
能
能
巩固练习
证明: 在△ADC 和△AEB 中,
∵AD =AE,∠A =∠A ,AC=AB,
∴△ADC≌△AEB (S.A.S.).
2. 如图,在△ABC中,AB = AC,在 AB、AC 上分别截取相等的两条线段 AD、AE,并连结 BE、CD. 求证:△ADC ≌△AEB.
新知讲解
如图,已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形.
此时(即“边边角”对应相等) 两个三角形不一定全等.
A
B
C
D
典例讲解
例2 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA,连结BC并延长到E,使CE=CB.连结DE,那么DE的长就是A、B的距离。你知道其中的道理吗
典例讲解
例2已知:AD与BE相交点C,CA=CD,CB=CE.
求证: AB = DE.
证明:在△ACB和△DCE中,
∵CA=CD(已知),
∠1 =∠2 (对顶角相等),
CB=CE(已知),
∴△ACB≌△DCE(S.A.S. ).
∴AB = DE (全等三角形的对应边相等).
巩固练习
3. 如图所示,小明想设计一种测零件内径 AB 的卡钳.在卡钳的设计中,要使测出的 DC 长度恰好为内径 AB 的长度,那么卡钳各部分的尺寸应满足什么条件呢?请提出你的想法.
解: 满足 OA = OC,OB=OD .
∵OA = OC,OB=OD ,∠AOB=∠COD ,
∴△AOB≌△COD (S.A.S.),
∴AB=CD .
课堂总结
边角边
判定定理
两边及其夹角分别相等的两个三角形全等
应用边角边证明全等,解决问题
应用
拓展提高
1、如图AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向终点B运动,同时点Q在线段BD由点B向终点D运动,则当点Q的运动速度为________cm/s时,能够在某一时刻使△ACB与△BPQ全等。
1.5或1
拓展提高
拓展提高
2、如图,在△ABC中,BE、CF分别是ACAB两边上的高,且它们交于点H,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG.
(1)求证:AD=AG
(2)判断AD与AG的位置关系,请说明理由。
拓展提高
拓展提高
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
