二次函数与一元二次方程(1)[下学期]
文档属性
| 名称 | 二次函数与一元二次方程(1)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 115.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-17 10:30:00 | ||
图片预览


文档简介
课件18张PPT。九年级数学(下)第二章 二次函数8. 二次函数与一元二次方程(1)
二次函数与一元二次方程的关系(1).h和t的关系式是什么?
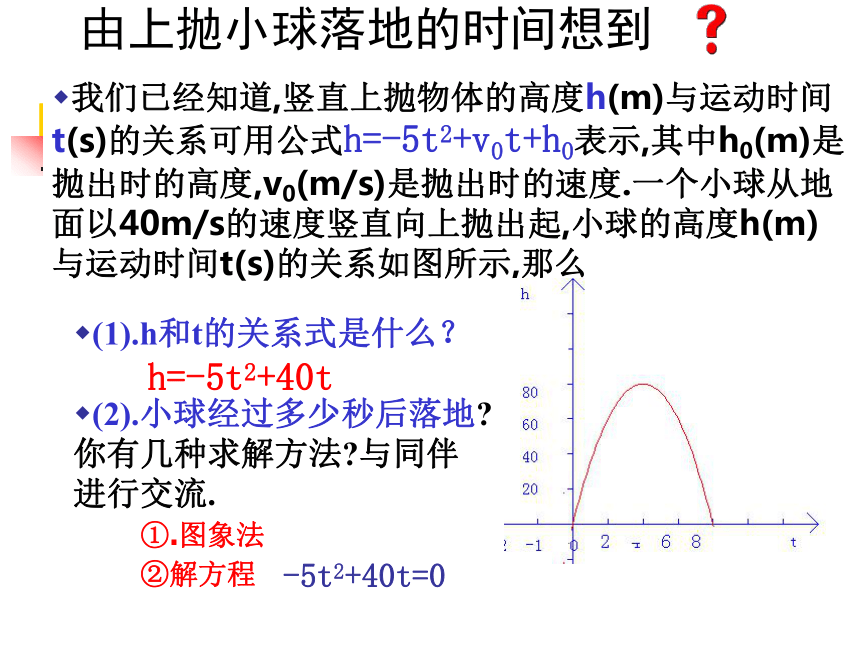
(2).小球经过多少秒后落地?你有几种求解方法?与同伴进行交流.由上抛小球落地的时间想到 我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么h=-5t2+40t①.图象法②解方程-5t2+40t=0(1).每个图象与x轴有几个交点?
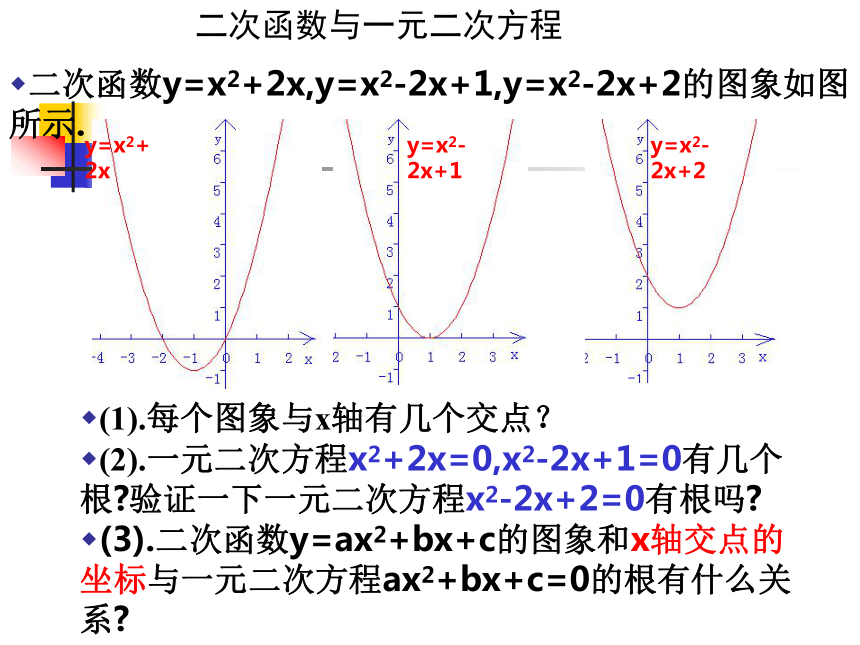
(2).一元二次方程x2+2x=0,x2-2x+1=0有几个根?验证一下一元二次方程x2-2x+2=0有根吗?
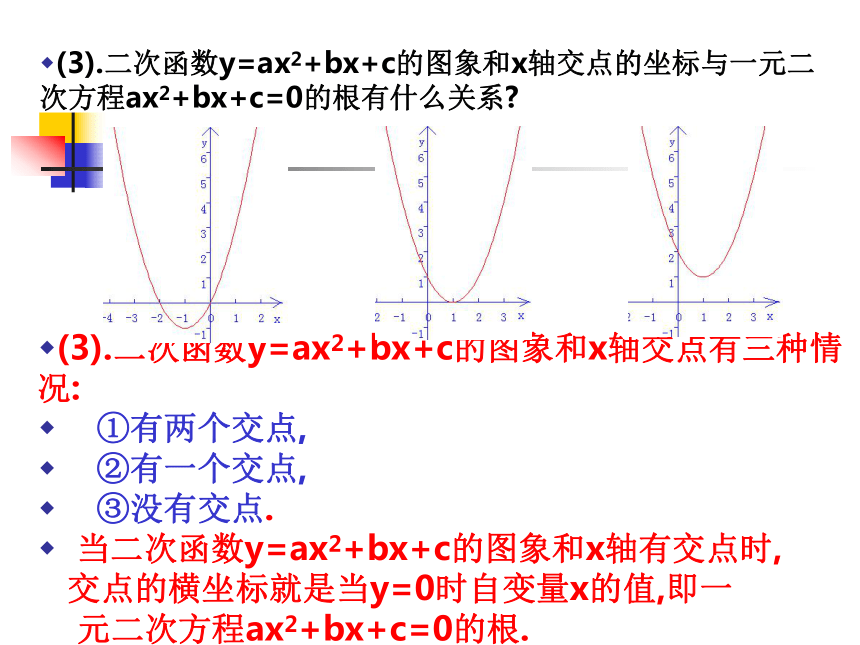
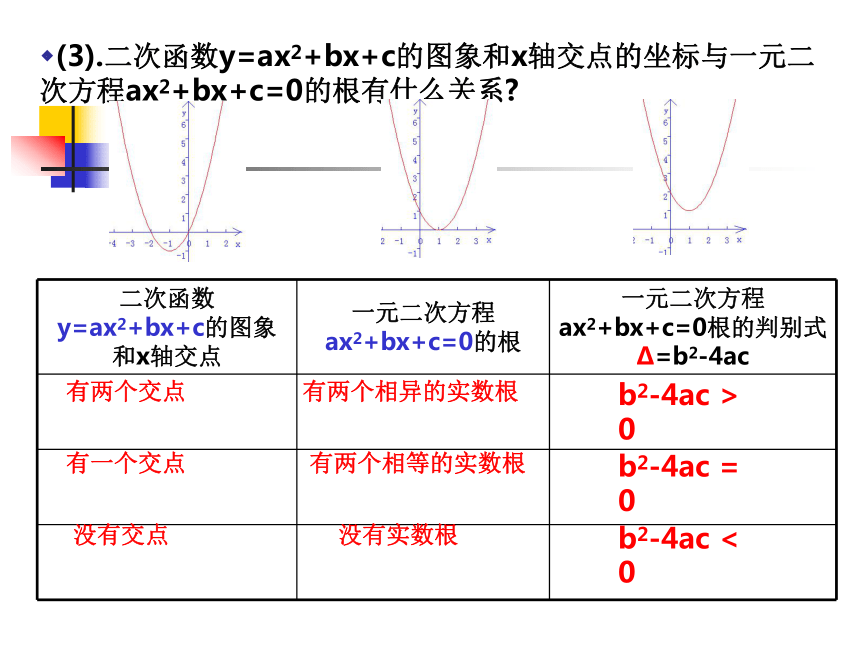
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数与一元二次方程 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.y=x2+2xy=x2-2x+1y=x2-2x+2(3).二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?一、探究探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)你发现方程 的解x1、x2与A、B的坐标有什么联系?x2-3x+2=0结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( ), B( )x1,0x2,0x(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0探究2、抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?△>0△=0
△<0OXY结论2:抛物线y=ax2+bx+c抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明: 1、△>0 一元二次方程ax2+bx+c=0
有两个不等的实数根与x轴有两个交点——相交。抛物线y=ax2+bx+c 2、△=0 一元二次方程ax2+bx+c=0
有两个相等的实数根与x轴有唯一公共点——相切(顶点)。抛物线y=ax2+bx+c 3、△<0 一元二次方程ax2+bx+c=0
没有实数根与x轴没有公共点——相离。探究3、若一元二次方程ax2+bx+c=0的两个根
是x1、x2,则由韦达定理得:x1+x2=-
x1x2=若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( x1,0 ), B(x2,0 ),则是否有同样的结论呢?
结论3、若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( x1,0 ), B(x2,0 ),
则x1+x2=- ,x1x2=
二、基础训练1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;3、已知抛物线y=x2+px+q与x轴的两个交点为(-2,0),(3,0),则p= ,q= 。2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点,则a的范围是 。评:若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( x1,0 ), B(x2,0 ),利用根与系数的关系,求证:A、B两点间的距离
AB=4、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+45. 已知抛物线 ,①求抛物线与y轴的交点坐标;②求抛物线与x轴的两个交点间的距离.6、抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0D7.已知二次函数y=-ax2,下列说法不正确的是( )
A.当a>0,x≠0时,y总取负值
B.当a<0,x<0时,y随x的增大而减小
C.当a<0时,函数图象有最低点,即y有最小值
D.当x<0,y= -ax2的对称轴是y轴D1、已知抛物线y=ax2+bx+c的顶点为(1,-4)与x轴两交点坐标分别为(x1,0),(x2,0),且x12+x22=10,求抛物线的解析式。三、例题推荐2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,
求m的值。2、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)k为何值时,二次函数y=x2-kx-2+k与轴两个交点A、B之间的距离最小?
(3)设此抛物线与y轴的交点为C,当k为6时,求S△ABC .3、已知抛物线y=-x2+2(m+1)x+m+3与x轴有两个交点A、B,其中A在x轴的正半轴,B在x轴的负半轴,
1)若OA=3OB,求m的值。
2)若3(OA-OB)=2OA·OB,求m的值。二次函数y=ax2+bx+c何时为一元二次方程?它们的关系如何?在本节一开始的小球上抛问题中,何时小球离地面的高度是60cm?你是如何知道的?四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。3、A、B两点间的距离AB= 。4、二次函数y=ax2+bx+c何时为一元二次方程?它们的关系如何?知识的升华P66 习题2.9 1,2题.
祝你成功!
二次函数与一元二次方程的关系(1).h和t的关系式是什么?
(2).小球经过多少秒后落地?你有几种求解方法?与同伴进行交流.由上抛小球落地的时间想到 我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么h=-5t2+40t①.图象法②解方程-5t2+40t=0(1).每个图象与x轴有几个交点?
(2).一元二次方程x2+2x=0,x2-2x+1=0有几个根?验证一下一元二次方程x2-2x+2=0有根吗?
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数与一元二次方程 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.y=x2+2xy=x2-2x+1y=x2-2x+2(3).二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?一、探究探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
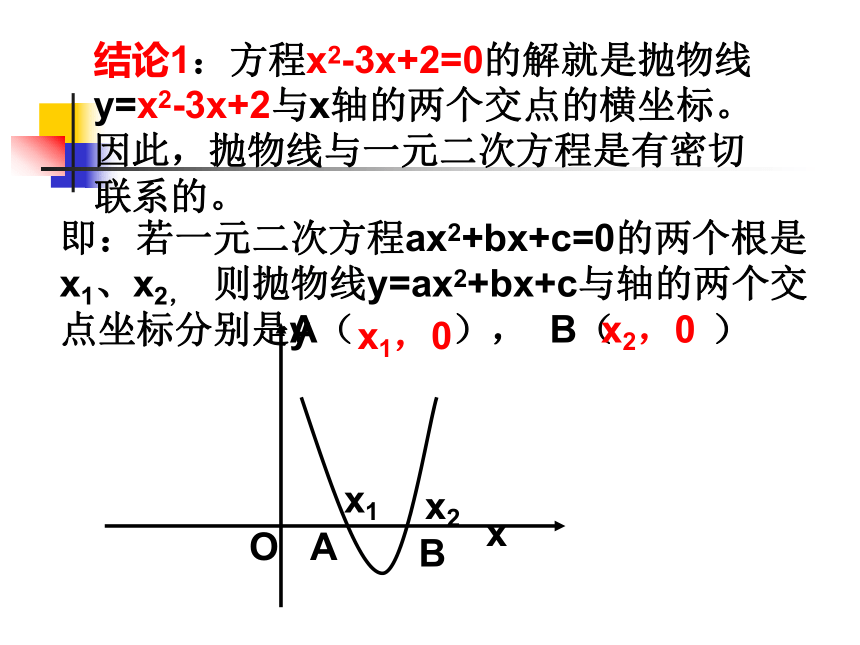
∴A(1,0) , B(2,0)你发现方程 的解x1、x2与A、B的坐标有什么联系?x2-3x+2=0结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( ), B( )x1,0x2,0x(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0探究2、抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?△>0△=0
△<0OXY结论2:抛物线y=ax2+bx+c抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明: 1、△>0 一元二次方程ax2+bx+c=0
有两个不等的实数根与x轴有两个交点——相交。抛物线y=ax2+bx+c 2、△=0 一元二次方程ax2+bx+c=0
有两个相等的实数根与x轴有唯一公共点——相切(顶点)。抛物线y=ax2+bx+c 3、△<0 一元二次方程ax2+bx+c=0
没有实数根与x轴没有公共点——相离。探究3、若一元二次方程ax2+bx+c=0的两个根
是x1、x2,则由韦达定理得:x1+x2=-
x1x2=若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( x1,0 ), B(x2,0 ),则是否有同样的结论呢?
结论3、若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( x1,0 ), B(x2,0 ),
则x1+x2=- ,x1x2=
二、基础训练1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;3、已知抛物线y=x2+px+q与x轴的两个交点为(-2,0),(3,0),则p= ,q= 。2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点,则a的范围是 。评:若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( x1,0 ), B(x2,0 ),利用根与系数的关系,求证:A、B两点间的距离
AB=4、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+45. 已知抛物线 ,①求抛物线与y轴的交点坐标;②求抛物线与x轴的两个交点间的距离.6、抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0D7.已知二次函数y=-ax2,下列说法不正确的是( )
A.当a>0,x≠0时,y总取负值
B.当a<0,x<0时,y随x的增大而减小
C.当a<0时,函数图象有最低点,即y有最小值
D.当x<0,y= -ax2的对称轴是y轴D1、已知抛物线y=ax2+bx+c的顶点为(1,-4)与x轴两交点坐标分别为(x1,0),(x2,0),且x12+x22=10,求抛物线的解析式。三、例题推荐2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,
求m的值。2、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)k为何值时,二次函数y=x2-kx-2+k与轴两个交点A、B之间的距离最小?
(3)设此抛物线与y轴的交点为C,当k为6时,求S△ABC .3、已知抛物线y=-x2+2(m+1)x+m+3与x轴有两个交点A、B,其中A在x轴的正半轴,B在x轴的负半轴,
1)若OA=3OB,求m的值。
2)若3(OA-OB)=2OA·OB,求m的值。二次函数y=ax2+bx+c何时为一元二次方程?它们的关系如何?在本节一开始的小球上抛问题中,何时小球离地面的高度是60cm?你是如何知道的?四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。3、A、B两点间的距离AB= 。4、二次函数y=ax2+bx+c何时为一元二次方程?它们的关系如何?知识的升华P66 习题2.9 1,2题.
祝你成功!
