23.2.1 中心对称 课件(共30张PPT)
文档属性
| 名称 | 23.2.1 中心对称 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 19:14:11 | ||
图片预览



文档简介
(共30张PPT)
23.2.1中心对称
人教版 九年级上册
1.理解中心对称的定义;
2.掌握中心对称的性质及其应用; (重点)
3.画出已知图形关于某一点的中心对称图形. (难点)
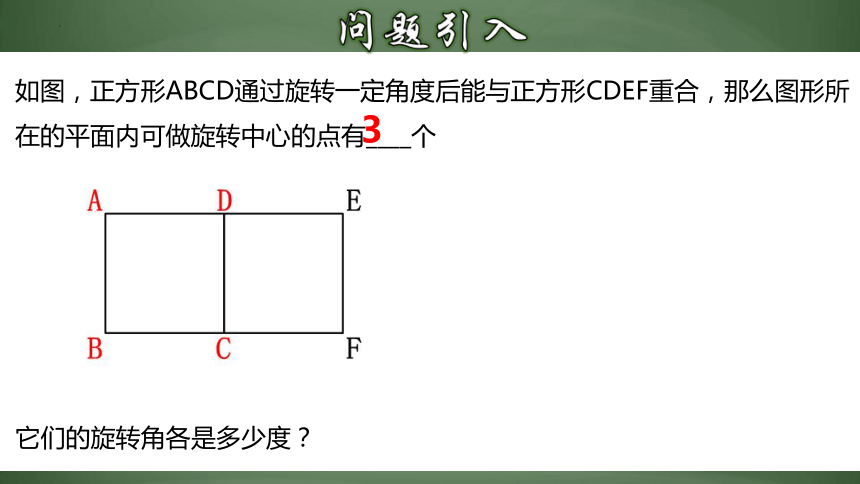
如图,正方形ABCD通过旋转一定角度后能与正方形CDEF重合,那么图形所在的平面内可做旋转中心的点有____个
3
它们的旋转角各是多少度?
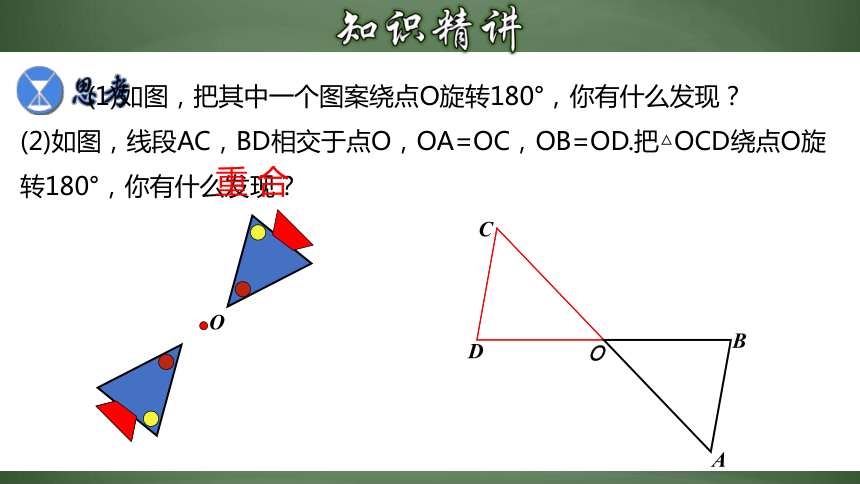
(1)如图,把其中一个图案绕点O旋转180°,你有什么发现?
(2)如图,线段AC,BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你有什么发现?
O
A
O
D
B
C
重 合
中心对称的定义
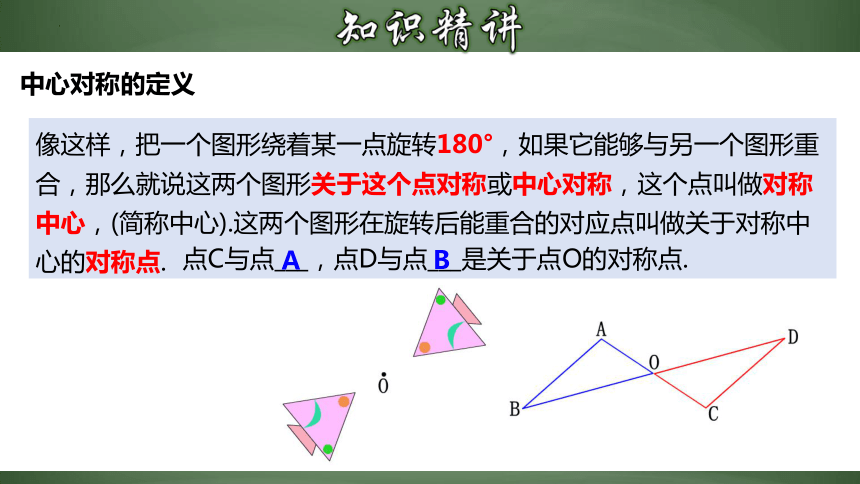
像这样,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
点C与点___,点D与点___是关于点O的对称点.
A
B
1.中心对称是一种特殊的旋转.其旋转角是180 °.
2.中心对称是两个图形之间一种特殊的位置关系.
要点理解:
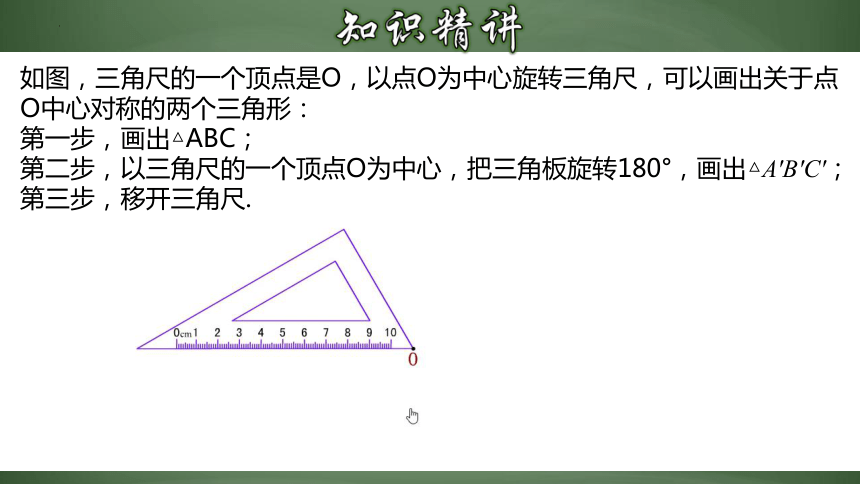
如图,三角尺的一个顶点是O,以点O为中心旋转三角尺,可以画出关于点O中心对称的两个三角形:
第一步,画出△ABC;
第二步,以三角尺的一个顶点O为中心,把三角板旋转180°,画出△A'B'C';
第三步,移开三角尺.
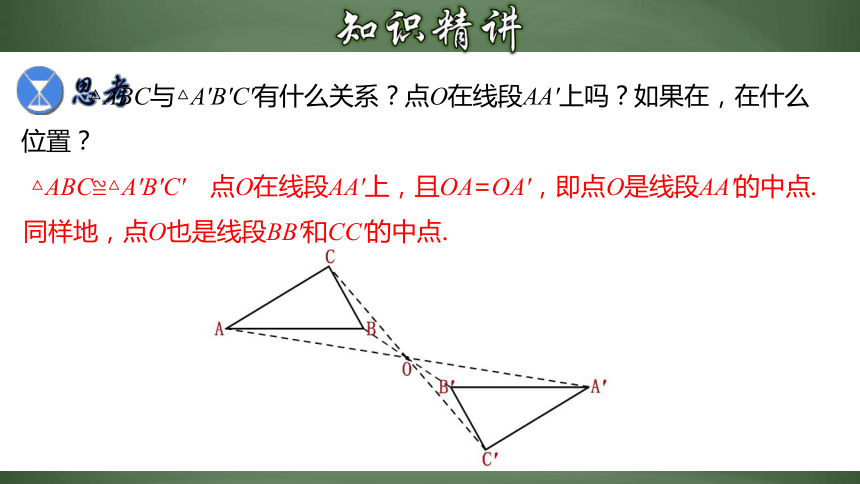
△ABC与△A'B'C'有什么关系?点O在线段AA'上吗?如果在,在什么位置?
△ABC≌△A'B'C' 点O在线段AA'上,且OA=OA',即点O是线段AA'的中点.同样地,点O也是线段BB'和CC'的中点.
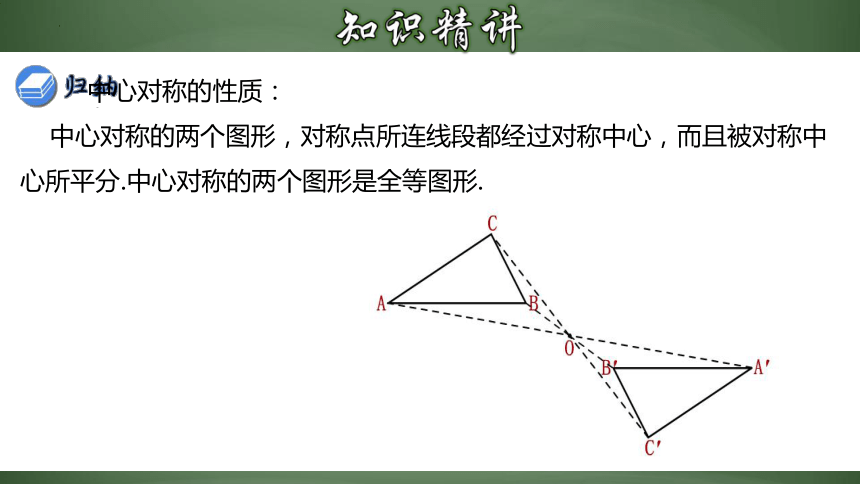
中心对称的性质:
中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.中心对称的两个图形是全等图形.
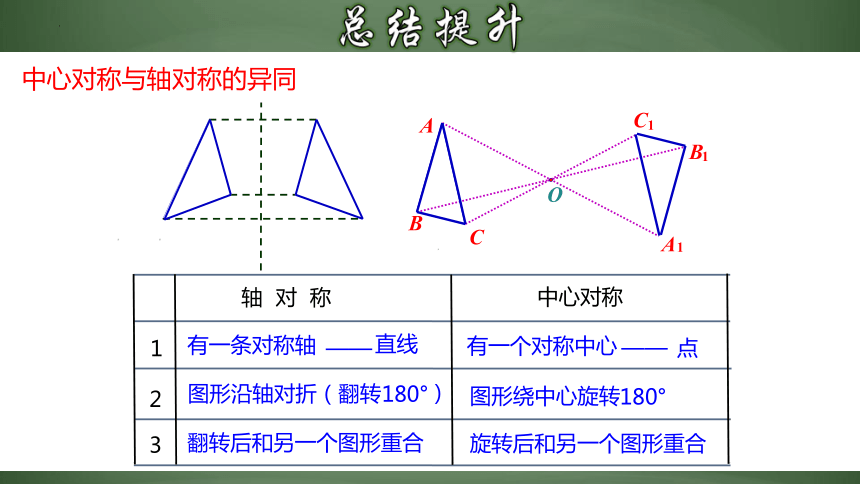
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
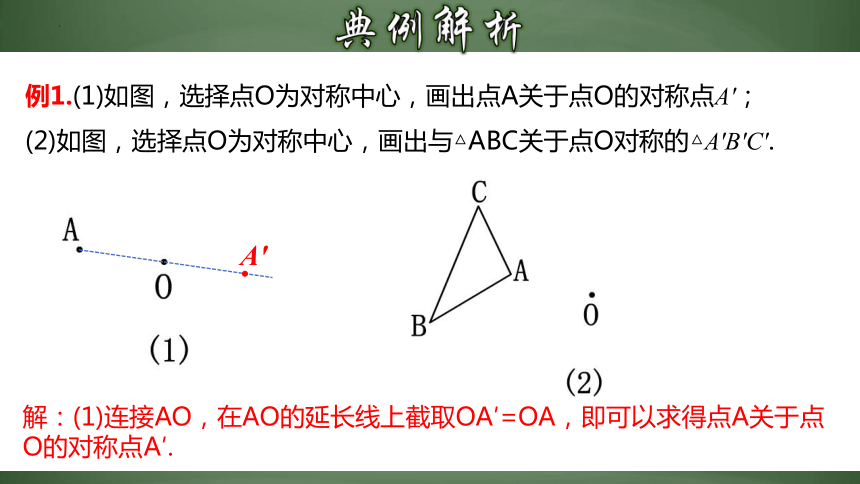
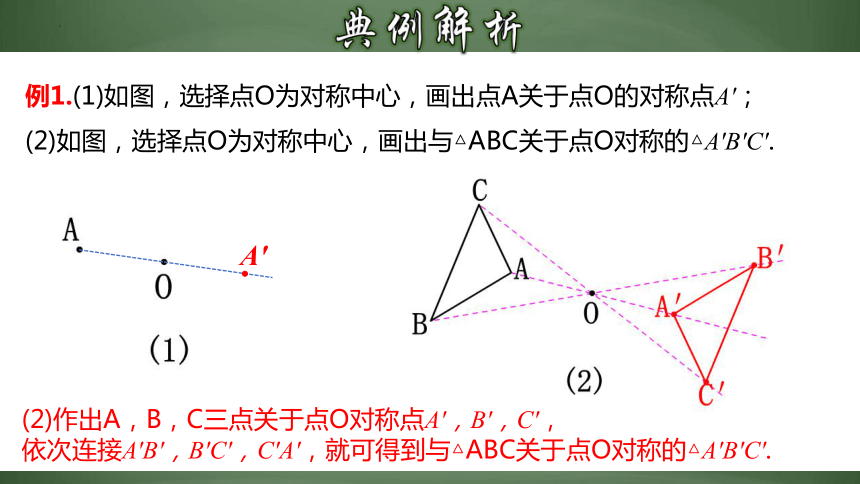
例1.(1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;
(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
A′
解:(1)连接AO,在AO的延长线上截取OA′=OA,即可以求得点A关于点O的对称点A′.
例1.(1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;
(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
A′
(2)作出A,B,C三点关于点O对称点A′,B′,C′,
依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于点O对称的△A′B′C′.
1.分别画出下列图形关于点O对称的图形.
2.图中的两个四边形关于某点对称,找出它们的对称中心.
解:如图,点O为它们的对称中心.
例2.如图,在边长为1的小正方形网格中,有一个,顶点坐标.
(1)将向左平移3个单位长度得到,请画出;
(2)画出关于点O成中心对称的;
(3)在(2)的条件下,求四边形的面积.
解:(1)如图所示,即为所求;
(2)如图所示,即为所求;
例2.如图,在边长为1的小正方形网格中,有一个,顶点坐标.
(1)将向左平移3个单位长度得到,请画出;
(2)画出关于点O成中心对称的;
(3)在(2)的条件下,求四边形的面积.
解:(3)如图所示,过点A和分别作轴的平行线,过点B和分别作轴的平行线,则所围成的四边形DEFG为正方形,
则S四边形 =S正方形DEFG
.
如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)画出关于原点对称的;
(2)求的面积.
(1)解:作图如下:
(2)解:.
例3.如图,正方形ABCD与正方形A'B'C'D’关于点O成中心对称.若正方形ABCD的边长为1,设图形重合部分的面积为y,线段0B的长为x,求y与x之 间的函数关系式.
解:如图,设CD与A'D'交于点E,AD与C'D'交于点F.
∵正方形ABCD与正方形A'B'C'D'关于点0成中心对称
∴四边形DED'F是正方形
∵正方形ABCD的边长为1,
∴BD=
∵0B=x,∴0D=BD-OB=-x
∴DE=(-x)=2-x
∴S正方形DED’=DE2=(2-x)2
∴y=2x2-4x+4
如图,与关于O点中心对称,点E、F在线段AC上,且AF=CE.
求证:FD=BE.
证明:∵△ABO与△CDO关于O点中心对称,∴OB=OD,OA=OC.
∵AF=CE,∴OF=OE.
∵在△DOF和△BOE中,,
∴△DOF≌△BOE(SAS).
∴FD=BE.
1.下列各组图形中,成中心对称的是( )
2.如图,如果甲、乙关于点0成中心对称,那么乙图中不符合题意的一块是( )
C
B
3.如图,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F.有以下结论:
①点E和F,点B和D是关于中心O的对称点;
②四边形DEOC与四边形OFBA的面积必相等;
③四边形ABCD是平行四边形;
④△AOE与△COF成中心对称.以上结论中,正确的个数为( )
A.1 B.2 C.3 D.4
D
4.如图,菱形ABCD的对角线AC、BD交于点O,AC=4, BD=16,将△BOC绕着点C旋转180°得到△B′O′C,则点A与点B′之间的距离为( )
A.6 B.8 C.10 D.12
C
5.如图(1),若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是____,点A的对称点是____,点E的对称点是____,连接A,F的线段经过____,且___________,△ABD≌_________.
6.如图(2),在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是__________.
点C
点F
点D
点C
AC=CF
△FGE
(3,-1)
7.如图①,已知△ABC与△ADE关于点A成中心对称,∠B=50°,△ABC的面积为24,BC边上的高为5.若将△ADE向下折叠,如图②,点D落在BC.上的G点处,点E落在CB的延长线上的H点处,且BH=4,则∠BAG=_____, S△ABG=_____.
8.如图,在△ABC中,AB=8,AC=6, AD为BC边上的中线,将△ADC绕点D旋转180°,得到△EDB,则中线AD长的取值范围是_____________.
80°
14
1<AD<7
9.画一个与已知四边形ABCD中心对称的图形.
(1)以顶点A为对称中心;(2)以BC边的中点为对称中心.
10.如图,在方格网中已知格点△ABC和点O.
(1)画出与△ABC关于点O对称的△A'B'C';
(2)若以点A、O、C'、 D为顶点的四边形是
平行四边形,请在方格网中标出所有符合条
件的D点,
解:(1)如图,△A'B'C'即为所求;
(2)如图,点D1、D2、D3即为所求点.
11.如图,已知 ABCD的对称中心在原点O,且A(﹣2,1),B(﹣3,﹣2).
(1)求C点及D点的坐标;
(2)求平行四边形ABCD的面积.
解:(1)∵四边形ABCD是平行四边形,
∴四边形ABCD关于O中心对称,
∵A(﹣2,1),B(﹣3,﹣2),
∴C(2,﹣1),D(3,2);
(2)设直线AB的解析式为:y=kx+b,
把A,B点代入得:
解得:
故y=3x+7,
当y=0时,x=,
由(1)得:A到x轴距离为:1,B到x轴距离为:2,∴SABCD=4×=14.
中心对称的定义
像这样,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
23.2.1中心对称
人教版 九年级上册
1.理解中心对称的定义;
2.掌握中心对称的性质及其应用; (重点)
3.画出已知图形关于某一点的中心对称图形. (难点)
如图,正方形ABCD通过旋转一定角度后能与正方形CDEF重合,那么图形所在的平面内可做旋转中心的点有____个
3
它们的旋转角各是多少度?
(1)如图,把其中一个图案绕点O旋转180°,你有什么发现?
(2)如图,线段AC,BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你有什么发现?
O
A
O
D
B
C
重 合
中心对称的定义
像这样,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
点C与点___,点D与点___是关于点O的对称点.
A
B
1.中心对称是一种特殊的旋转.其旋转角是180 °.
2.中心对称是两个图形之间一种特殊的位置关系.
要点理解:
如图,三角尺的一个顶点是O,以点O为中心旋转三角尺,可以画出关于点O中心对称的两个三角形:
第一步,画出△ABC;
第二步,以三角尺的一个顶点O为中心,把三角板旋转180°,画出△A'B'C';
第三步,移开三角尺.
△ABC与△A'B'C'有什么关系?点O在线段AA'上吗?如果在,在什么位置?
△ABC≌△A'B'C' 点O在线段AA'上,且OA=OA',即点O是线段AA'的中点.同样地,点O也是线段BB'和CC'的中点.
中心对称的性质:
中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.中心对称的两个图形是全等图形.
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
例1.(1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;
(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
A′
解:(1)连接AO,在AO的延长线上截取OA′=OA,即可以求得点A关于点O的对称点A′.
例1.(1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;
(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
A′
(2)作出A,B,C三点关于点O对称点A′,B′,C′,
依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于点O对称的△A′B′C′.
1.分别画出下列图形关于点O对称的图形.
2.图中的两个四边形关于某点对称,找出它们的对称中心.
解:如图,点O为它们的对称中心.
例2.如图,在边长为1的小正方形网格中,有一个,顶点坐标.
(1)将向左平移3个单位长度得到,请画出;
(2)画出关于点O成中心对称的;
(3)在(2)的条件下,求四边形的面积.
解:(1)如图所示,即为所求;
(2)如图所示,即为所求;
例2.如图,在边长为1的小正方形网格中,有一个,顶点坐标.
(1)将向左平移3个单位长度得到,请画出;
(2)画出关于点O成中心对称的;
(3)在(2)的条件下,求四边形的面积.
解:(3)如图所示,过点A和分别作轴的平行线,过点B和分别作轴的平行线,则所围成的四边形DEFG为正方形,
则S四边形 =S正方形DEFG
.
如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)画出关于原点对称的;
(2)求的面积.
(1)解:作图如下:
(2)解:.
例3.如图,正方形ABCD与正方形A'B'C'D’关于点O成中心对称.若正方形ABCD的边长为1,设图形重合部分的面积为y,线段0B的长为x,求y与x之 间的函数关系式.
解:如图,设CD与A'D'交于点E,AD与C'D'交于点F.
∵正方形ABCD与正方形A'B'C'D'关于点0成中心对称
∴四边形DED'F是正方形
∵正方形ABCD的边长为1,
∴BD=
∵0B=x,∴0D=BD-OB=-x
∴DE=(-x)=2-x
∴S正方形DED’=DE2=(2-x)2
∴y=2x2-4x+4
如图,与关于O点中心对称,点E、F在线段AC上,且AF=CE.
求证:FD=BE.
证明:∵△ABO与△CDO关于O点中心对称,∴OB=OD,OA=OC.
∵AF=CE,∴OF=OE.
∵在△DOF和△BOE中,,
∴△DOF≌△BOE(SAS).
∴FD=BE.
1.下列各组图形中,成中心对称的是( )
2.如图,如果甲、乙关于点0成中心对称,那么乙图中不符合题意的一块是( )
C
B
3.如图,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F.有以下结论:
①点E和F,点B和D是关于中心O的对称点;
②四边形DEOC与四边形OFBA的面积必相等;
③四边形ABCD是平行四边形;
④△AOE与△COF成中心对称.以上结论中,正确的个数为( )
A.1 B.2 C.3 D.4
D
4.如图,菱形ABCD的对角线AC、BD交于点O,AC=4, BD=16,将△BOC绕着点C旋转180°得到△B′O′C,则点A与点B′之间的距离为( )
A.6 B.8 C.10 D.12
C
5.如图(1),若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是____,点A的对称点是____,点E的对称点是____,连接A,F的线段经过____,且___________,△ABD≌_________.
6.如图(2),在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是__________.
点C
点F
点D
点C
AC=CF
△FGE
(3,-1)
7.如图①,已知△ABC与△ADE关于点A成中心对称,∠B=50°,△ABC的面积为24,BC边上的高为5.若将△ADE向下折叠,如图②,点D落在BC.上的G点处,点E落在CB的延长线上的H点处,且BH=4,则∠BAG=_____, S△ABG=_____.
8.如图,在△ABC中,AB=8,AC=6, AD为BC边上的中线,将△ADC绕点D旋转180°,得到△EDB,则中线AD长的取值范围是_____________.
80°
14
1<AD<7
9.画一个与已知四边形ABCD中心对称的图形.
(1)以顶点A为对称中心;(2)以BC边的中点为对称中心.
10.如图,在方格网中已知格点△ABC和点O.
(1)画出与△ABC关于点O对称的△A'B'C';
(2)若以点A、O、C'、 D为顶点的四边形是
平行四边形,请在方格网中标出所有符合条
件的D点,
解:(1)如图,△A'B'C'即为所求;
(2)如图,点D1、D2、D3即为所求点.
11.如图,已知 ABCD的对称中心在原点O,且A(﹣2,1),B(﹣3,﹣2).
(1)求C点及D点的坐标;
(2)求平行四边形ABCD的面积.
解:(1)∵四边形ABCD是平行四边形,
∴四边形ABCD关于O中心对称,
∵A(﹣2,1),B(﹣3,﹣2),
∴C(2,﹣1),D(3,2);
(2)设直线AB的解析式为:y=kx+b,
把A,B点代入得:
解得:
故y=3x+7,
当y=0时,x=,
由(1)得:A到x轴距离为:1,B到x轴距离为:2,∴SABCD=4×=14.
中心对称的定义
像这样,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
