23.2.3关于原点对称的点的坐标 课件(共25张PPT)
文档属性
| 名称 | 23.2.3关于原点对称的点的坐标 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 19:14:48 | ||
图片预览






文档简介
(共25张PPT)
关于原点对称的点的坐标
人教版 九年级上册
学习目标
1.会在平面直角坐标系内作关于原点对称的图形;(重点)
2.掌握两点关于原点对称时,横纵坐标的关系;(难点)
3.进一步体会数形结合的思想.
新知导入
在平面直角坐标系中,关于x轴对称的点横坐标_______,纵坐标______________;关于y轴对称的点横坐标_____________,纵坐标__________.
点(x,y)关于x轴对称的点的坐标为(___,___)
点(x,y)关于y轴对称的点的坐标为(___,___)
相等
互为相反数
互为相反数
相等
x -y
-x y
新知探究
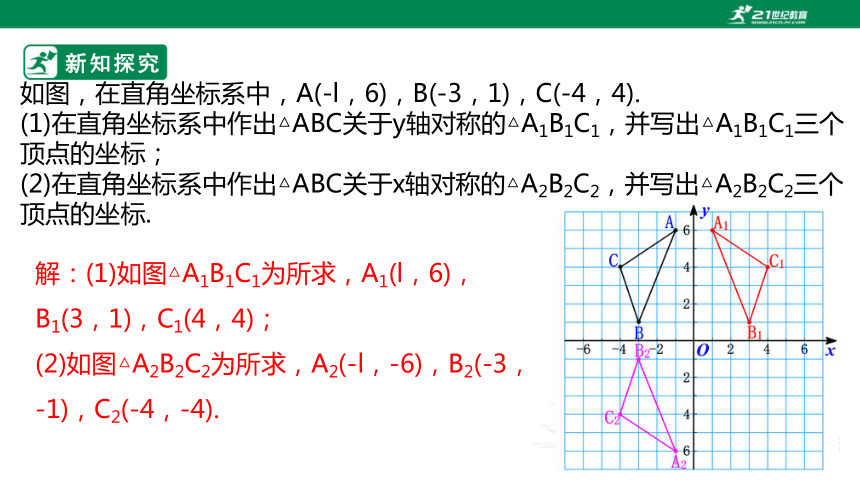
如图,在直角坐标系中,A(-l,6),B(-3,1),C(-4,4).
(1)在直角坐标系中作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
(2)在直角坐标系中作出△ABC关于x轴对称的△A2B2C2,并写出△A2B2C2三个顶点的坐标.
解:(1)如图△A1B1C1为所求,A1(l,6),B1(3,1),C1(4,4);
(2)如图△A2B2C2为所求,A2(-l,-6),B2(-3,-1),C2(-4,-4).
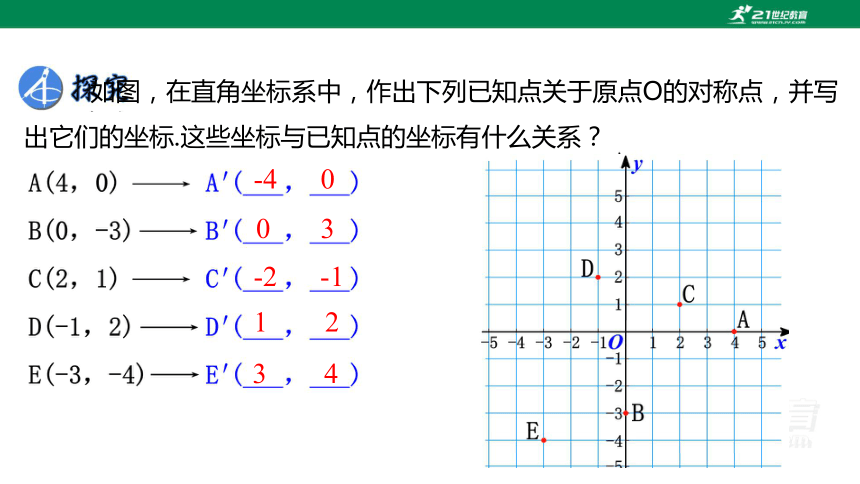
如图,在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.这些坐标与已知点的坐标有什么关系?
-4 0
0 3
-2 -1
1 2
3 4
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P′(-x,-y).
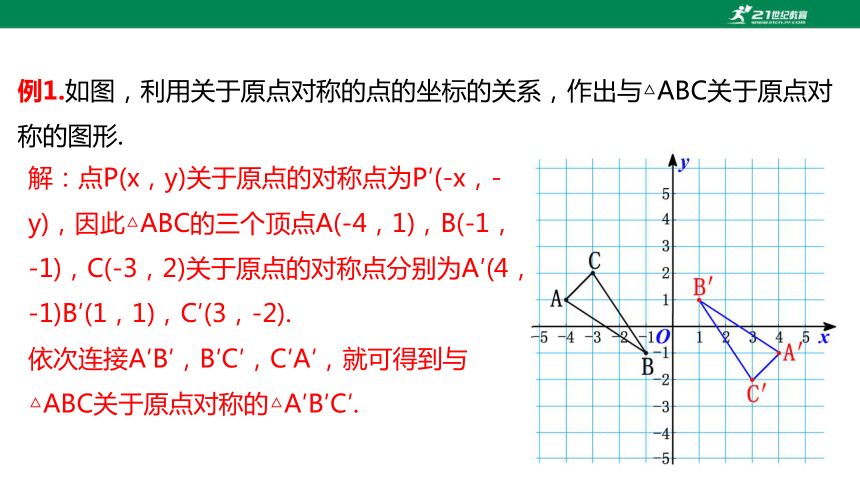
例1.如图,利用关于原点对称的点的坐标的关系,作出与△ABC关于原点对称的图形.
解:点P(x,y)关于原点的对称点为P′(-x,-y),因此△ABC的三个顶点A(-4,1),B(-1,-1),C(-3,2)关于原点的对称点分别为A′(4,-1)B′(1,1),C′(3,-2).
依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于原点对称的△A′B′C′.
作关于原点对称的图形的一般步骤:
(1)写出各点关于原点对称的点的坐标;
(2)在坐标平面内描出这些对称点;
(3)参照原图形顺次连接各点,即为所求作的对称图形.
例2.如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点上,点A的坐标是(1, -4).
(1)作出△ABC关于原点O对称的△A1B1C1;
(2)将△A1B1C1向右平移5个单位长度,得到
△A2B2C2,画出△A2B2C2;
(3)如果△ABC可以通过一次旋转得到△A2B2C2,
则旋转中心的坐标是 .
例2.如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点上,点A的坐标是(1, -4).
(1)作出△ABC关于原点O对称的△A1B1C1;
(1)解:∵由图可知:A(2,-2), B(1,-4), C(4,-3),
∴A1(-2,2), B1 (-1,4), C1 (-4,3),
如图所示:△A1B1C1,即为所求;
例2.如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点上,点A的坐标是(1, -4).
(2)将△A1B1C1向右平移5个单位长度,得到
△A2B2C2,画出△A2B2C2;
(2)解:∵由图可知:A1(-2,2), B1 (-1,4), C1 (-4,3),
∴将△A1B1C1向右平移5个单位长度,得到A2 (3,2), B2 (4,4), C2 (1,3),
如图所示:△A2B2C2,即为所求;
例2.如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点上,点A的坐标是(1, -4).
(3)如果△ABC可以通过一次旋转得到△A2B2C2,
则旋转中心的坐标是 .
(3)解:如图连接AA2,CC2,线段AA2与线段CC2交点即为所求,旋转中心坐标为(2.5,0)
例3.如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B、C的坐标为(2,1)、(6,1),∠BAC=90°, AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为_________.
【分析】由已知条件易得A(4, 3)
由A(4,3)、B(2,1)可得yAB=x-1
∴P(1,0)
∵A与A‘关于点P成中心对称
∴
∴A'(-2, -3)
(-2,-3)
课堂练习
1.平面直角坐标系中,与点(2,-3)关于原点中心对称的点是( )
A.(-3,2) B.(3,-2) C.(-2,3) D.(2,3)
2.在平面直角坐标系中,将点(2,-5)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,-5) B.(-4,5) C.(-4,-5) D.(0,-5)
3.在平面直角坐标系中,点P(-20, a)与点Q(b, 13)关于原点对称,则a+b的值为( )
A.33 B.-33 C.-7 D.7
C
B
D
课堂练习
4.己知点P1(a, -3)和P2(-4, b)关于x轴对称,则(a+b)2000的值为( )
A.1 B.-1 C.72000 D.-72000
5.已知点P的坐标为(2-a, 3a+6), 且点P到两坐标轴的距离相等,则点P关于原点0对称点的坐标为( )
A.(-3,3) B.(-3,-3) C.(-6, 6) D.(-3, -3)或(-6,6)
A
D
6.在平面直角坐标系中,已知点P(a,b)(|a|≠|b|),设点P关于直线y=x的对称点为Q,点P关于原点的对称点为R,则△PQR的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
B
7.已知点M的坐标为(3,-4), 则关于x轴对称的点N的坐标为________,关于y轴对称的点P的坐标为________,关于原点对称的点Q的坐示为________.
8.点P1(a-1,5)和P2(-2, b-1)关于原点对称,则ab=_____.
9.已知点P(3a-9,1-a)是第三象限的点,且横、纵坐标均为整数.若P、Q关于原点对称,点Q的坐标为________.
(3,4)
(-3,-4)
(-3,4)
12
(3,1)
10.如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点A坐标是(a, b), 则经过第2025次变换后所得的A点坐标是_________.
(a,b)
11.已知点A(2m+n,2),B(1,n﹣m).
(1)m、n为何值时,点A、B关于y轴对称?
(2)m、n为何值时,点A、B关于原点中心对称?
解:(1)∵点A(2m+n,2),B(1,n-m),A、B关于y轴对称,
∴,
解得:;
11.已知点A(2m+n,2),B(1,n﹣m).
(1)m、n为何值时,点A、B关于y轴对称?
(2)m、n为何值时,点A、B关于原点中心对称?
解:(2)∵点A(2m+n,2),B(1,n-m),A、B关于原点中心对称,
∴,
解得:.
12.如图,已知点A的坐标为(-2 ,2),点B的坐标为(-1,-),菱形ABCD的对角线交于坐标原点O.求C,D两点的坐标.
解:依题意可知,点A与点C关于原点对称,点B与点D关于原点对称,
因此,点C(2 ,-2)点D(1,).
13.如图,在平面直角坐标系中,已知ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3)
(1)画出ABC关于原点O的中心对称图
形 ;
(2)若点P为y轴上一动点,则PA+PC的
最小值为______.
解:(1)如图, 即为所求,
(2)作点A关于y轴对称点,连接C交y轴于点P,此时PA+PC的值最小,如上图,
由图像可得最小值=C=,
课堂小结
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P′(-x,-y).
作关于原点对称的图形的一般步骤:
(1)写出各点关于原点对称的点的坐标;
(2)在坐标平面内描出这些对称点;
(3)参照原图形顺次连接各点,即为所求作的对称图形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
关于原点对称的点的坐标
人教版 九年级上册
学习目标
1.会在平面直角坐标系内作关于原点对称的图形;(重点)
2.掌握两点关于原点对称时,横纵坐标的关系;(难点)
3.进一步体会数形结合的思想.
新知导入
在平面直角坐标系中,关于x轴对称的点横坐标_______,纵坐标______________;关于y轴对称的点横坐标_____________,纵坐标__________.
点(x,y)关于x轴对称的点的坐标为(___,___)
点(x,y)关于y轴对称的点的坐标为(___,___)
相等
互为相反数
互为相反数
相等
x -y
-x y
新知探究
如图,在直角坐标系中,A(-l,6),B(-3,1),C(-4,4).
(1)在直角坐标系中作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
(2)在直角坐标系中作出△ABC关于x轴对称的△A2B2C2,并写出△A2B2C2三个顶点的坐标.
解:(1)如图△A1B1C1为所求,A1(l,6),B1(3,1),C1(4,4);
(2)如图△A2B2C2为所求,A2(-l,-6),B2(-3,-1),C2(-4,-4).
如图,在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.这些坐标与已知点的坐标有什么关系?
-4 0
0 3
-2 -1
1 2
3 4
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P′(-x,-y).
例1.如图,利用关于原点对称的点的坐标的关系,作出与△ABC关于原点对称的图形.
解:点P(x,y)关于原点的对称点为P′(-x,-y),因此△ABC的三个顶点A(-4,1),B(-1,-1),C(-3,2)关于原点的对称点分别为A′(4,-1)B′(1,1),C′(3,-2).
依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于原点对称的△A′B′C′.
作关于原点对称的图形的一般步骤:
(1)写出各点关于原点对称的点的坐标;
(2)在坐标平面内描出这些对称点;
(3)参照原图形顺次连接各点,即为所求作的对称图形.
例2.如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点上,点A的坐标是(1, -4).
(1)作出△ABC关于原点O对称的△A1B1C1;
(2)将△A1B1C1向右平移5个单位长度,得到
△A2B2C2,画出△A2B2C2;
(3)如果△ABC可以通过一次旋转得到△A2B2C2,
则旋转中心的坐标是 .
例2.如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点上,点A的坐标是(1, -4).
(1)作出△ABC关于原点O对称的△A1B1C1;
(1)解:∵由图可知:A(2,-2), B(1,-4), C(4,-3),
∴A1(-2,2), B1 (-1,4), C1 (-4,3),
如图所示:△A1B1C1,即为所求;
例2.如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点上,点A的坐标是(1, -4).
(2)将△A1B1C1向右平移5个单位长度,得到
△A2B2C2,画出△A2B2C2;
(2)解:∵由图可知:A1(-2,2), B1 (-1,4), C1 (-4,3),
∴将△A1B1C1向右平移5个单位长度,得到A2 (3,2), B2 (4,4), C2 (1,3),
如图所示:△A2B2C2,即为所求;
例2.如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点上,点A的坐标是(1, -4).
(3)如果△ABC可以通过一次旋转得到△A2B2C2,
则旋转中心的坐标是 .
(3)解:如图连接AA2,CC2,线段AA2与线段CC2交点即为所求,旋转中心坐标为(2.5,0)
例3.如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B、C的坐标为(2,1)、(6,1),∠BAC=90°, AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为_________.
【分析】由已知条件易得A(4, 3)
由A(4,3)、B(2,1)可得yAB=x-1
∴P(1,0)
∵A与A‘关于点P成中心对称
∴
∴A'(-2, -3)
(-2,-3)
课堂练习
1.平面直角坐标系中,与点(2,-3)关于原点中心对称的点是( )
A.(-3,2) B.(3,-2) C.(-2,3) D.(2,3)
2.在平面直角坐标系中,将点(2,-5)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,-5) B.(-4,5) C.(-4,-5) D.(0,-5)
3.在平面直角坐标系中,点P(-20, a)与点Q(b, 13)关于原点对称,则a+b的值为( )
A.33 B.-33 C.-7 D.7
C
B
D
课堂练习
4.己知点P1(a, -3)和P2(-4, b)关于x轴对称,则(a+b)2000的值为( )
A.1 B.-1 C.72000 D.-72000
5.已知点P的坐标为(2-a, 3a+6), 且点P到两坐标轴的距离相等,则点P关于原点0对称点的坐标为( )
A.(-3,3) B.(-3,-3) C.(-6, 6) D.(-3, -3)或(-6,6)
A
D
6.在平面直角坐标系中,已知点P(a,b)(|a|≠|b|),设点P关于直线y=x的对称点为Q,点P关于原点的对称点为R,则△PQR的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
B
7.已知点M的坐标为(3,-4), 则关于x轴对称的点N的坐标为________,关于y轴对称的点P的坐标为________,关于原点对称的点Q的坐示为________.
8.点P1(a-1,5)和P2(-2, b-1)关于原点对称,则ab=_____.
9.已知点P(3a-9,1-a)是第三象限的点,且横、纵坐标均为整数.若P、Q关于原点对称,点Q的坐标为________.
(3,4)
(-3,-4)
(-3,4)
12
(3,1)
10.如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点A坐标是(a, b), 则经过第2025次变换后所得的A点坐标是_________.
(a,b)
11.已知点A(2m+n,2),B(1,n﹣m).
(1)m、n为何值时,点A、B关于y轴对称?
(2)m、n为何值时,点A、B关于原点中心对称?
解:(1)∵点A(2m+n,2),B(1,n-m),A、B关于y轴对称,
∴,
解得:;
11.已知点A(2m+n,2),B(1,n﹣m).
(1)m、n为何值时,点A、B关于y轴对称?
(2)m、n为何值时,点A、B关于原点中心对称?
解:(2)∵点A(2m+n,2),B(1,n-m),A、B关于原点中心对称,
∴,
解得:.
12.如图,已知点A的坐标为(-2 ,2),点B的坐标为(-1,-),菱形ABCD的对角线交于坐标原点O.求C,D两点的坐标.
解:依题意可知,点A与点C关于原点对称,点B与点D关于原点对称,
因此,点C(2 ,-2)点D(1,).
13.如图,在平面直角坐标系中,已知ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3)
(1)画出ABC关于原点O的中心对称图
形 ;
(2)若点P为y轴上一动点,则PA+PC的
最小值为______.
解:(1)如图, 即为所求,
(2)作点A关于y轴对称点,连接C交y轴于点P,此时PA+PC的值最小,如上图,
由图像可得最小值=C=,
课堂小结
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P′(-x,-y).
作关于原点对称的图形的一般步骤:
(1)写出各点关于原点对称的点的坐标;
(2)在坐标平面内描出这些对称点;
(3)参照原图形顺次连接各点,即为所求作的对称图形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
