二次函数与一元二次方程(2)[下学期]
文档属性
| 名称 | 二次函数与一元二次方程(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 283.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-12-19 00:00:00 | ||
图片预览


文档简介
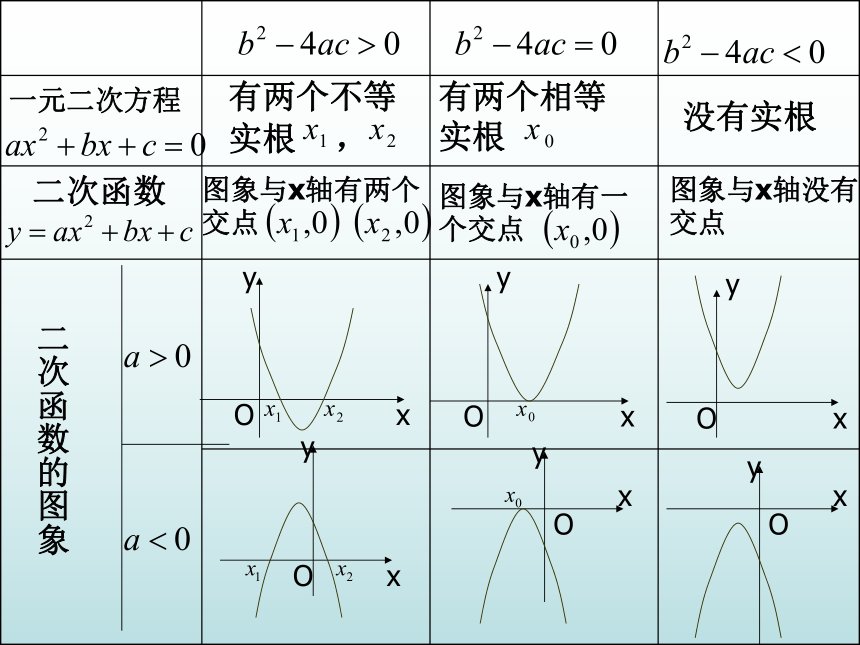
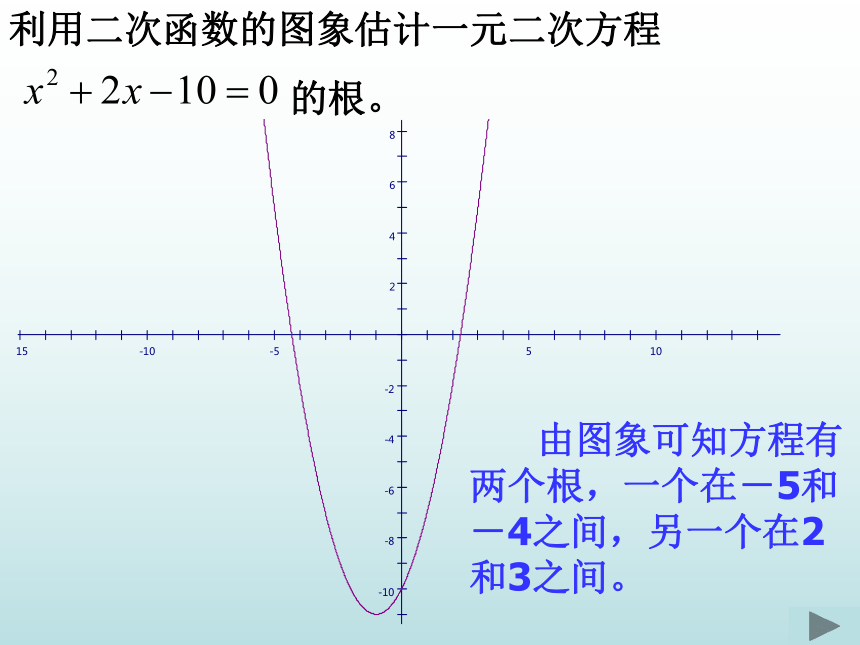
课件10张PPT。二次函数与一元二次方程(2)没有实根一元二次方程二次函数二次函数的图象图象与x轴没有交点探究示例,潜能开发例1、利用二次函数图象求方程x2+2x–10=0的根(精确到十分位)解(1)作出函数y=x2+2x–10的图象; (2)由图象可知,方程有两个根,一个根在–5和
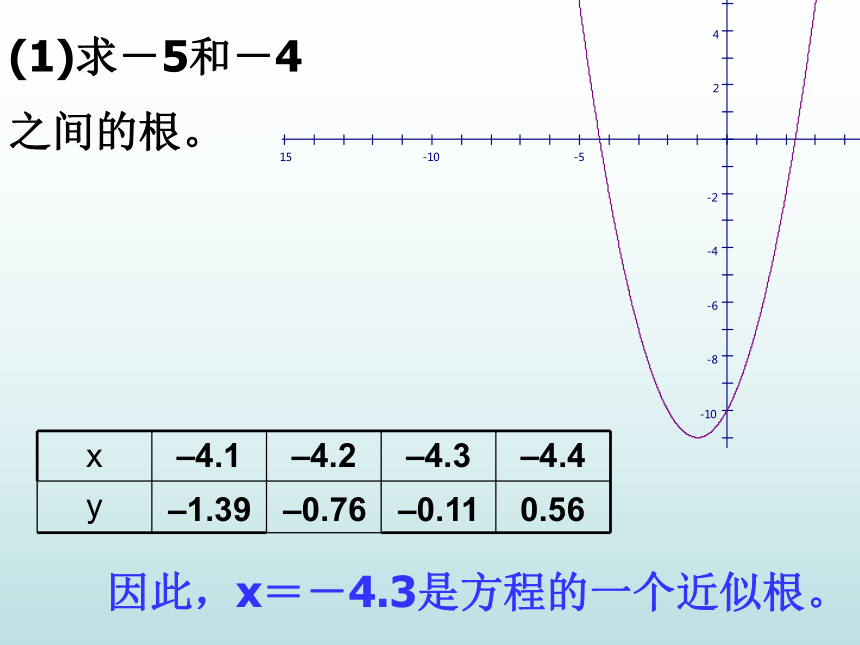
–4之间,一个在2和3之间。 (3)探求其解的十分位数 由图象可知方程有两个根,一个在-5和-4之间,另一个在2和3之间。(1)求-5和-4
之间的根。因此,x=-4.3是方程的一个近似根。–1.39–0.76–0.110.56(2)求2和3之间的根。因此,x=2.3是方程的一个近似根。–1.39–0.76–0.110.56所以方程的两个近似根分别为–4.3和2.3(1).用描点法作二次函数y=x2+2x-10的图象;一元二次方程的图象解法 利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.(2).观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程x2+2x-10=3的解;由此可知,方程x2+2x-10=3的近似根为:
x1≈-4.7,x2≈2.7.(2). 作直线y=3;(1).原方程可变形为x2+2x-13=0;一元二次方程的图象解法 利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.(2).观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程x2+2x-10=3的解;由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.(2).用描点法作二次函数y=x2+2x-13的图象;;知识的升华P72 习题2.9 1题.
作业本
祝你成功!结束寄语不知道并不可怕和有害,任何人都不可能什么都知道,可怕的和有害的是不知道而伪装知道.再见
–4之间,一个在2和3之间。 (3)探求其解的十分位数 由图象可知方程有两个根,一个在-5和-4之间,另一个在2和3之间。(1)求-5和-4
之间的根。因此,x=-4.3是方程的一个近似根。–1.39–0.76–0.110.56(2)求2和3之间的根。因此,x=2.3是方程的一个近似根。–1.39–0.76–0.110.56所以方程的两个近似根分别为–4.3和2.3(1).用描点法作二次函数y=x2+2x-10的图象;一元二次方程的图象解法 利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.(2).观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程x2+2x-10=3的解;由此可知,方程x2+2x-10=3的近似根为:
x1≈-4.7,x2≈2.7.(2). 作直线y=3;(1).原方程可变形为x2+2x-13=0;一元二次方程的图象解法 利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.(2).观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程x2+2x-10=3的解;由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.(2).用描点法作二次函数y=x2+2x-13的图象;;知识的升华P72 习题2.9 1题.
作业本
祝你成功!结束寄语不知道并不可怕和有害,任何人都不可能什么都知道,可怕的和有害的是不知道而伪装知道.再见
