13.3.2等边三角形(第2课时)
文档属性
| 名称 | 13.3.2等边三角形(第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 593.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-29 19:27:47 | ||
图片预览


文档简介
课件15张PPT。知识回顾:(1).等边三角形的性质
1.等边三角形的内角都相等,且都等于60 °
2.等边三角形是轴对称图形,有三条对称轴
3.等边三角形各边上中线,高和所对角的平分线都三线合一.
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
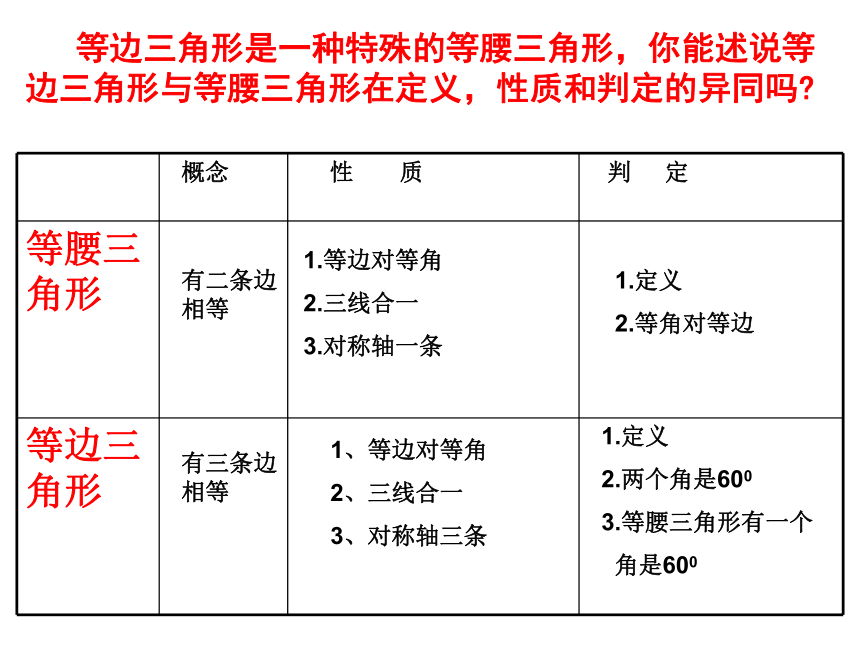
3.有一个内角等于60 °的等腰三角形是等边三角形.(2) 等边三角形的判定: 等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?有二条边相等1.等边对等角
2.三线合一
3.对称轴一条1、等边对等角
2、三线合一
3、对称轴三条有三条边相等1.定义
2.等角对等边1.定义
2.两个角是600
3.等腰三角形有一个
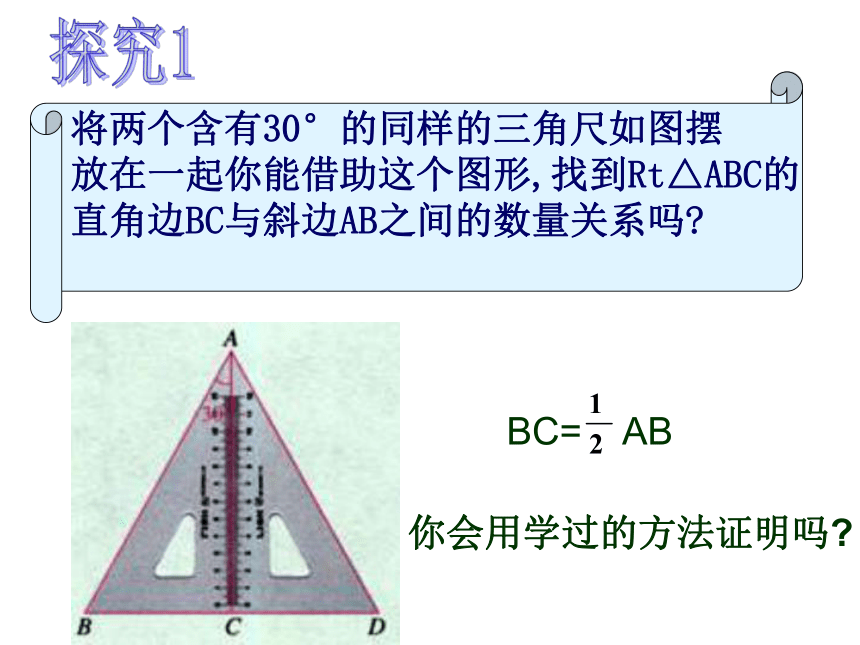
角是600将两个含有30°的同样的三角尺如图摆
放在一起你能借助这个图形,找到Rt△ABC的
直角边BC与斜边AB之间的数量关系吗?
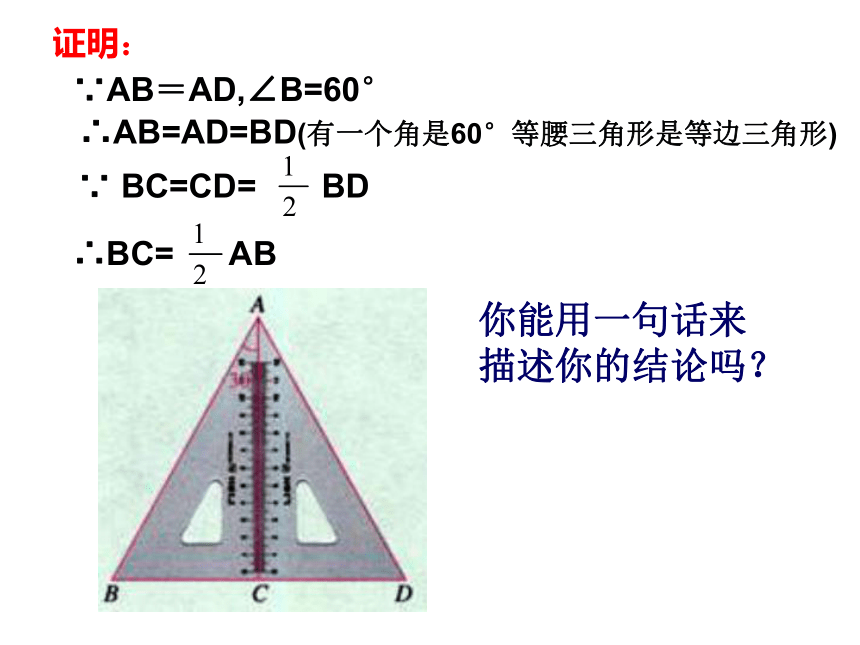
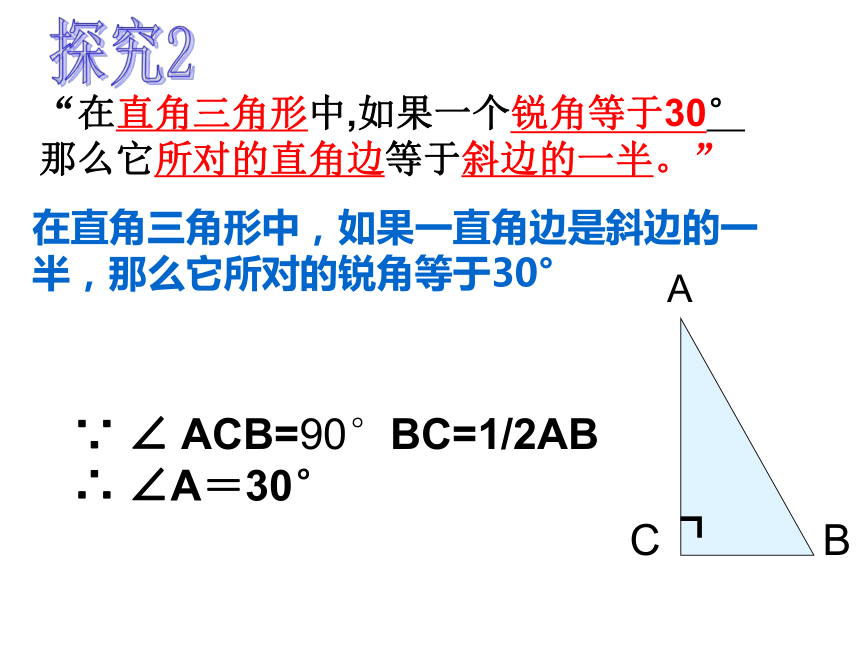
BC= AB你会用学过的方法证明吗?∵AB=AD,∠B=60°∴AB=AD=BD(有一个角是60°等腰三角形是等边三角形) ∵ BC=CD= BD∴BC= AB证明:在直角三角形中,如果一个锐角等于30°
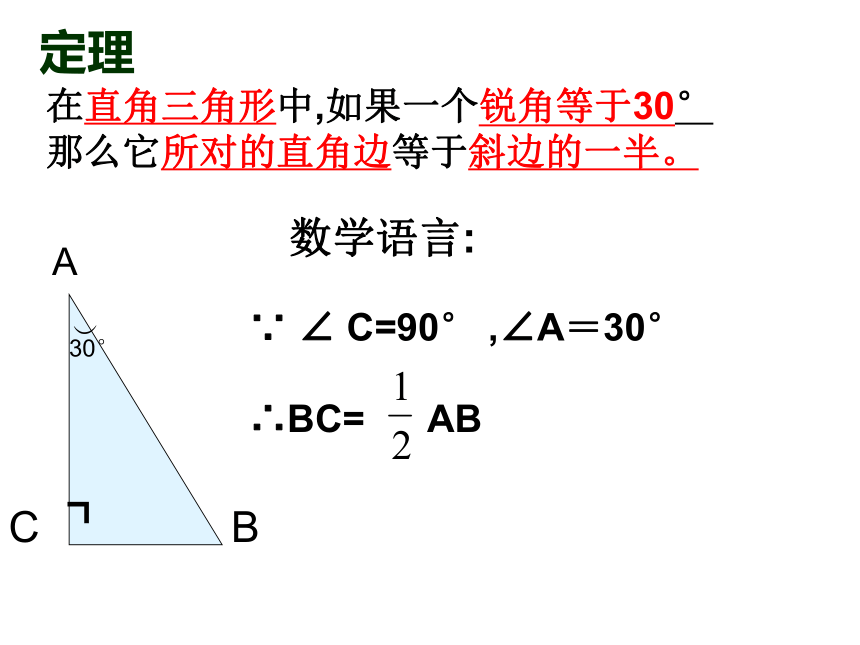
那么它所对的直角边等于斜边的一半。数学语言:∵ ∠ C=90° ,∠A=30°
∴BC= AB定理在直角三角形中,如果一直角边是斜边的一半,那么它所对的锐角等于30°“在直角三角形中,如果一个锐角等于30°
那么它所对的直角边等于斜边的一半。” 例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°立柱BC、DE要多长?
解: ∵DE⊥AC,BC⊥AC, ∠A= 30 °
由上述定理可得:
BC=1/2AB,DE=1/2AD,
∴BC=1/2×7.4=3.7(m)
又AD=1/2AB=1/2×7.4=3.7(m)
∴DE=1/2AD=1/2×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.1.如图:在Rt△ABC中,∠A=300,AB+BC=12cm
则AB=_____cm82.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm, BD=___, BE=____4cm 2cm3、如图,在△ABC中, ∠ACB= 90°,BA的垂直平分线交边CB于D。若AB=10,AC=5,则图中等于 30°的角的个数为( )
A.2 B.3 C.4 D.5B′解:过C作BA延长线的垂线CD,垂足为D
∵∠B=∠ACB=150(已知),
∴∠DAC=∠B+∠ACB= 150+150=300
∴CD= AC= ×2a=a
(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半).ACBD150150例2.已知:等腰三角形的底角为150,腰长为2a.
求:腰上的高.2a
特殊的直角三角形的性质:
定理1:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
定理2:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.小结谢谢!
1.等边三角形的内角都相等,且都等于60 °
2.等边三角形是轴对称图形,有三条对称轴
3.等边三角形各边上中线,高和所对角的平分线都三线合一.
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.(2) 等边三角形的判定: 等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?有二条边相等1.等边对等角
2.三线合一
3.对称轴一条1、等边对等角
2、三线合一
3、对称轴三条有三条边相等1.定义
2.等角对等边1.定义
2.两个角是600
3.等腰三角形有一个
角是600将两个含有30°的同样的三角尺如图摆
放在一起你能借助这个图形,找到Rt△ABC的
直角边BC与斜边AB之间的数量关系吗?
BC= AB你会用学过的方法证明吗?∵AB=AD,∠B=60°∴AB=AD=BD(有一个角是60°等腰三角形是等边三角形) ∵ BC=CD= BD∴BC= AB证明:在直角三角形中,如果一个锐角等于30°
那么它所对的直角边等于斜边的一半。数学语言:∵ ∠ C=90° ,∠A=30°
∴BC= AB定理在直角三角形中,如果一直角边是斜边的一半,那么它所对的锐角等于30°“在直角三角形中,如果一个锐角等于30°
那么它所对的直角边等于斜边的一半。” 例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°立柱BC、DE要多长?
解: ∵DE⊥AC,BC⊥AC, ∠A= 30 °
由上述定理可得:
BC=1/2AB,DE=1/2AD,
∴BC=1/2×7.4=3.7(m)
又AD=1/2AB=1/2×7.4=3.7(m)
∴DE=1/2AD=1/2×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.1.如图:在Rt△ABC中,∠A=300,AB+BC=12cm
则AB=_____cm82.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm, BD=___, BE=____4cm 2cm3、如图,在△ABC中, ∠ACB= 90°,BA的垂直平分线交边CB于D。若AB=10,AC=5,则图中等于 30°的角的个数为( )
A.2 B.3 C.4 D.5B′解:过C作BA延长线的垂线CD,垂足为D
∵∠B=∠ACB=150(已知),
∴∠DAC=∠B+∠ACB= 150+150=300
∴CD= AC= ×2a=a
(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半).ACBD150150例2.已知:等腰三角形的底角为150,腰长为2a.
求:腰上的高.2a
特殊的直角三角形的性质:
定理1:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
定理2:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.小结谢谢!
