13.3.1.等腰三角形
文档属性
| 名称 | 13.3.1.等腰三角形 |

|
|
| 格式 | zip | ||
| 文件大小 | 965.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-29 00:00:00 | ||
图片预览



文档简介
课件29张PPT。13.3.1等腰三角形
情景导入图中有些你熟悉的图形吗?
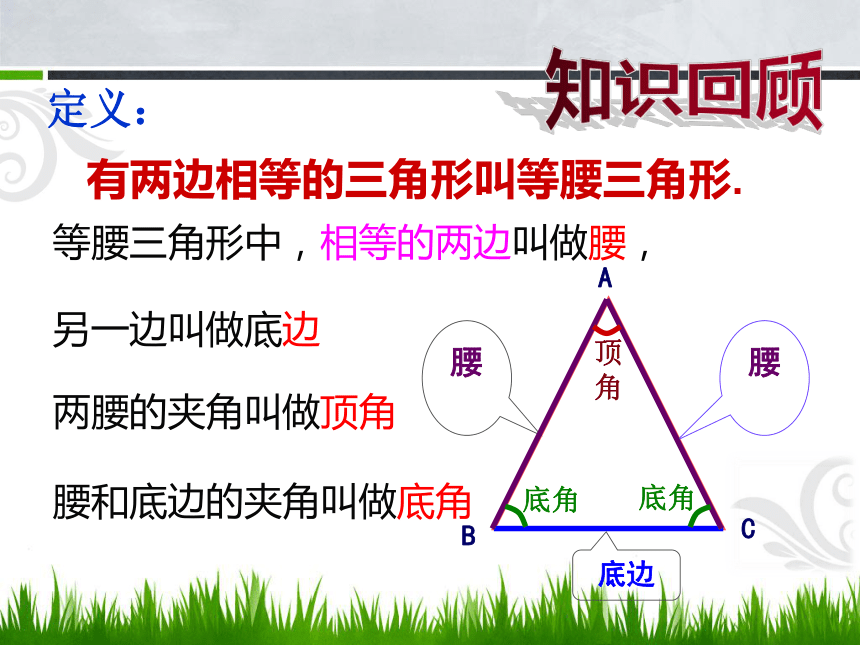
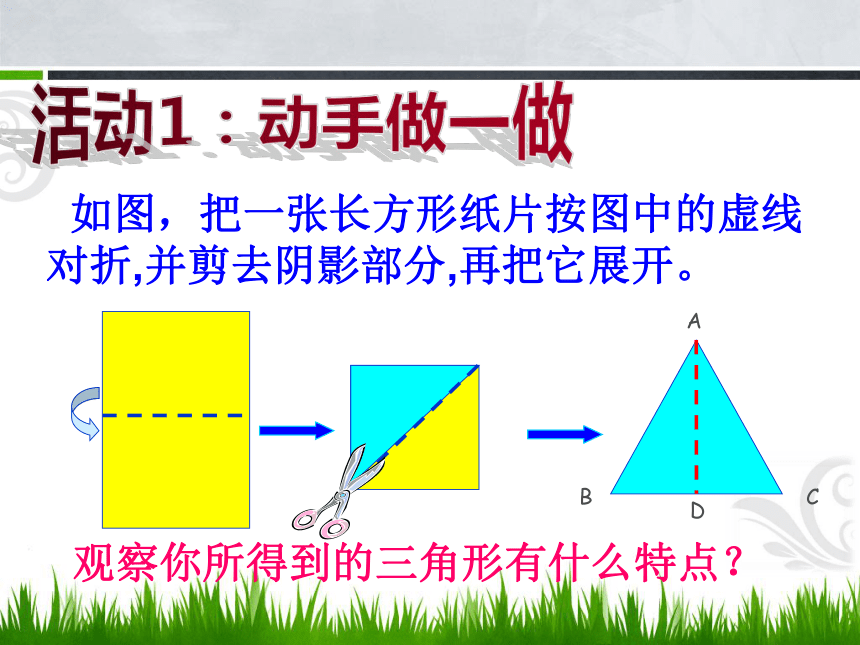
图中有些你熟悉的图形吗?它们有什么共同特点?北京五塔寺西安半坡博物馆斜拉桥梁体育观看台架埃及金字塔底角底角底边顶角腰和底边的夹角叫做底角有两边相等的三角形叫等腰三角形.定义:等腰三角形中,相等的两边叫做腰,另一边叫做底边两腰的夹角叫做顶角知识回顾活动1:动手做一做 如图,把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展开。观察你所得到的三角形有什么特点?ABCD
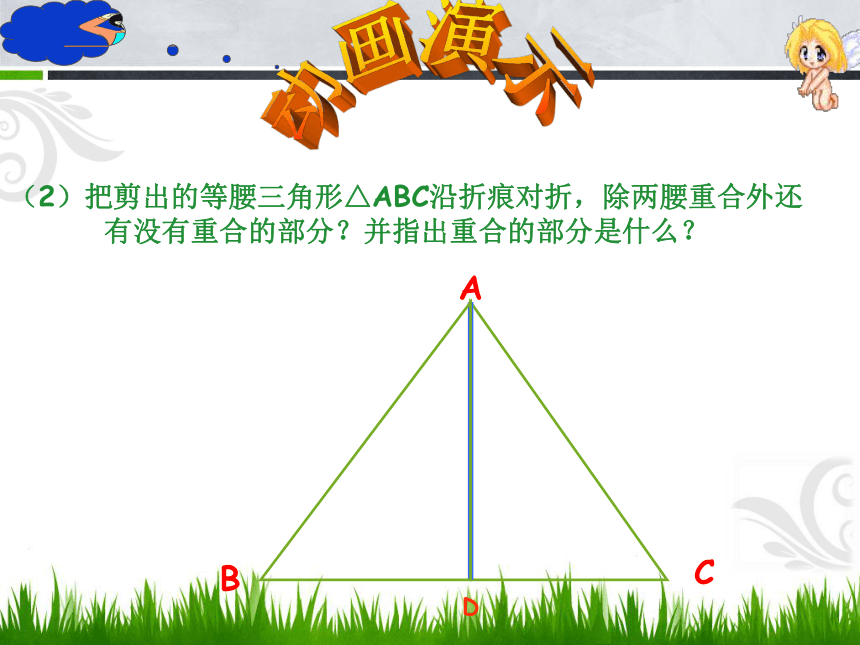
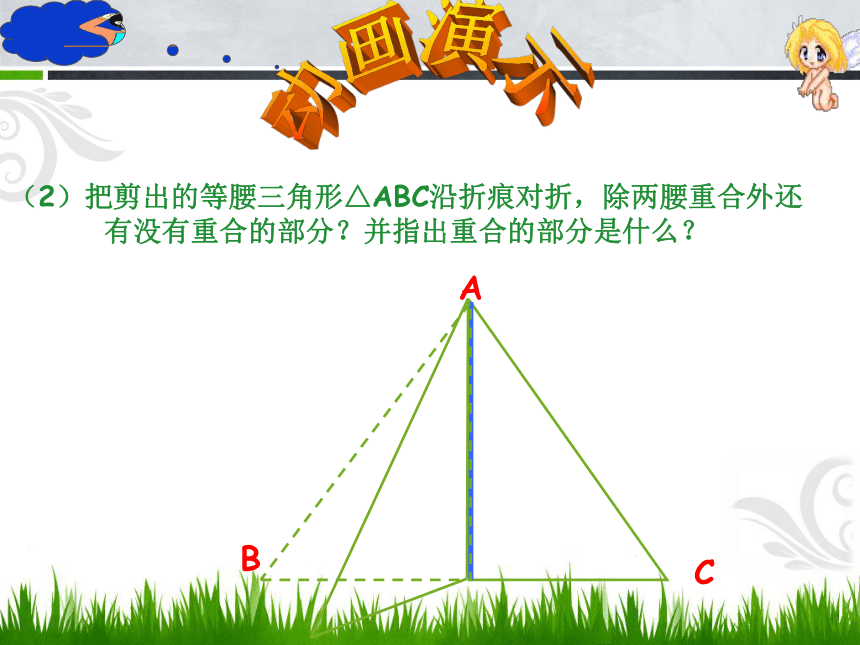
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? D
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示AC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? 底角 如图所示,AD为折痕,找出图中相等的角和相等的线段。1. ∠ B =∠ C2. BD = CD4. ∠ADB = ∠ADC = 90°3. ∠BAD = ∠CADAD 为底边上的中线AD为顶角平分线AD为底边上的高活动2:探索等腰三角形的性质由上面的结论猜一猜等腰三角形有什么性质?2.等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合.1 .等腰三角形的两个底角相等 是不是任意等腰三角形都具有这样的性质呢?我们用几何画板来验证一下大家动手来证明!已知:在△ABC中,AB=AC,求证∠B=∠C等腰三角形的两个底角相等D证明:作底边BC的中线AD∴ △ADB≌△ADC∴ ∠B=∠C在△ADB和△ADC中∴BD=CD已知:在△ABC中,AB=AC,求证∠B=∠C等腰三角形的两个底角相等2.等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合.1 .等腰三角形的两个底角相等等腰三角形的性质 一般三角形有没有这样的性质呢?D(等边对等角)(三线合一)几何画板展示例1、如图,在△ABC中,AB = AC,点D在AC上,且BD=BC=AD.(1)图中共有哪些等腰三角形.
(2)求△ABC各内角的度数。解: (1) △ABC、△BDC、△ABD(2)设∠A=x(1)∵AB=AC,AD是边BC上的高,
∴∠_____ = ∠_____,____= ____. (2) ∵AB=AC,AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AB=AC,AD是角平分线,
∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCDD如图所示,利用等腰三角形的性质2填空1.在△ABC中,AB = AC,∠A = 50°,
则∠B = .2.在△ABC中,AB = AC,∠B= 50°,
则∠A= .65°80°小试牛刀3.等腰三角形一个角为70°,它的另外两个角为______________70°,40°或55°,55°30°,30°4.等腰三角形一个角为120°,它的另外两个角为______例2、如图,在△ABC中,AB=AC,BD=CD,AD的延长线交BC于E.求证:AE⊥BC.∴ △ADB≌△ADC∴ ∠BAD=∠CAD证明:在△ADB和△ADC中∴ AE⊥BC又∵ AB=AC等腰三角形的性质:3)等腰三角形的底边上的中线,底边上的高
和顶角平分线、互相重合(三线合一)2)等腰三角形的两底角相等(等边对等角)1)等腰三角形是轴对称图形小结
小结:通过本节课的学习你有收获吗?1.本节主要教学知识是等腰三角形的两个性质。等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的
两个底角相等 等腰三角形的顶角
平分线、底边上的
中线底边上的高
互相重合。∵AB=AC(已知)
∴∠B=∠C (等边对等角)①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
② ∵AB=AC,BD=DC(已知)
∴ ∠1=∠2, AD⊥BC(三线合一)
③∵ AB=AC, AD⊥BC (已知)
∴ ∠1=∠2, BD=DC(三线合一)D122、本节课学习了数学思想及方法:分类讨论和一题多解。1.课本77页练习题2.练习册37—38页Thanks!
情景导入图中有些你熟悉的图形吗?
图中有些你熟悉的图形吗?它们有什么共同特点?北京五塔寺西安半坡博物馆斜拉桥梁体育观看台架埃及金字塔底角底角底边顶角腰和底边的夹角叫做底角有两边相等的三角形叫等腰三角形.定义:等腰三角形中,相等的两边叫做腰,另一边叫做底边两腰的夹角叫做顶角知识回顾活动1:动手做一做 如图,把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展开。观察你所得到的三角形有什么特点?ABCD
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? D
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示AC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? 底角 如图所示,AD为折痕,找出图中相等的角和相等的线段。1. ∠ B =∠ C2. BD = CD4. ∠ADB = ∠ADC = 90°3. ∠BAD = ∠CADAD 为底边上的中线AD为顶角平分线AD为底边上的高活动2:探索等腰三角形的性质由上面的结论猜一猜等腰三角形有什么性质?2.等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合.1 .等腰三角形的两个底角相等 是不是任意等腰三角形都具有这样的性质呢?我们用几何画板来验证一下大家动手来证明!已知:在△ABC中,AB=AC,求证∠B=∠C等腰三角形的两个底角相等D证明:作底边BC的中线AD∴ △ADB≌△ADC∴ ∠B=∠C在△ADB和△ADC中∴BD=CD已知:在△ABC中,AB=AC,求证∠B=∠C等腰三角形的两个底角相等2.等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合.1 .等腰三角形的两个底角相等等腰三角形的性质 一般三角形有没有这样的性质呢?D(等边对等角)(三线合一)几何画板展示例1、如图,在△ABC中,AB = AC,点D在AC上,且BD=BC=AD.(1)图中共有哪些等腰三角形.
(2)求△ABC各内角的度数。解: (1) △ABC、△BDC、△ABD(2)设∠A=x(1)∵AB=AC,AD是边BC上的高,
∴∠_____ = ∠_____,____= ____. (2) ∵AB=AC,AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AB=AC,AD是角平分线,
∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCDD如图所示,利用等腰三角形的性质2填空1.在△ABC中,AB = AC,∠A = 50°,
则∠B = .2.在△ABC中,AB = AC,∠B= 50°,
则∠A= .65°80°小试牛刀3.等腰三角形一个角为70°,它的另外两个角为______________70°,40°或55°,55°30°,30°4.等腰三角形一个角为120°,它的另外两个角为______例2、如图,在△ABC中,AB=AC,BD=CD,AD的延长线交BC于E.求证:AE⊥BC.∴ △ADB≌△ADC∴ ∠BAD=∠CAD证明:在△ADB和△ADC中∴ AE⊥BC又∵ AB=AC等腰三角形的性质:3)等腰三角形的底边上的中线,底边上的高
和顶角平分线、互相重合(三线合一)2)等腰三角形的两底角相等(等边对等角)1)等腰三角形是轴对称图形小结
小结:通过本节课的学习你有收获吗?1.本节主要教学知识是等腰三角形的两个性质。等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的
两个底角相等 等腰三角形的顶角
平分线、底边上的
中线底边上的高
互相重合。∵AB=AC(已知)
∴∠B=∠C (等边对等角)①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
② ∵AB=AC,BD=DC(已知)
∴ ∠1=∠2, AD⊥BC(三线合一)
③∵ AB=AC, AD⊥BC (已知)
∴ ∠1=∠2, BD=DC(三线合一)D122、本节课学习了数学思想及方法:分类讨论和一题多解。1.课本77页练习题2.练习册37—38页Thanks!
