圆的对称性(一)[下学期]
图片预览




文档简介
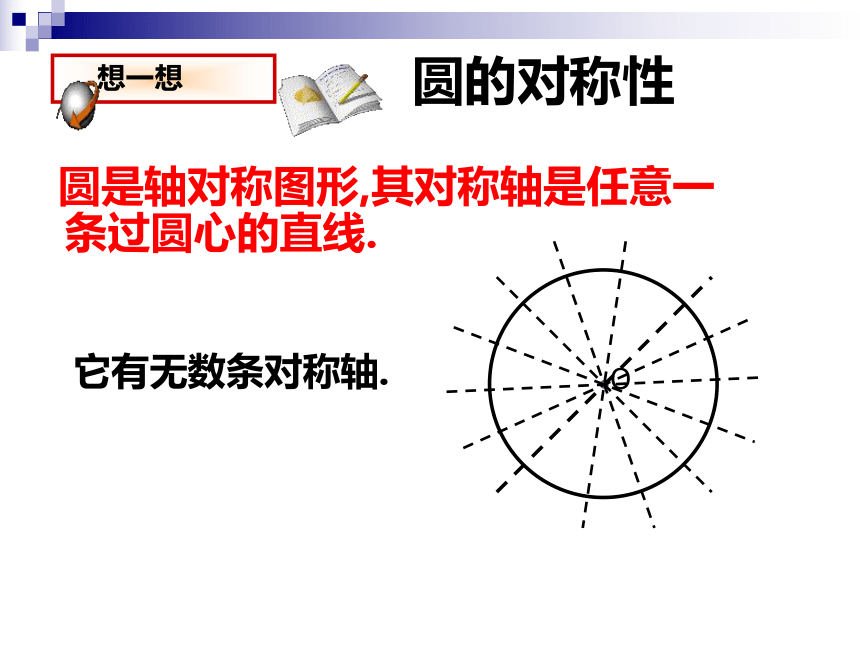
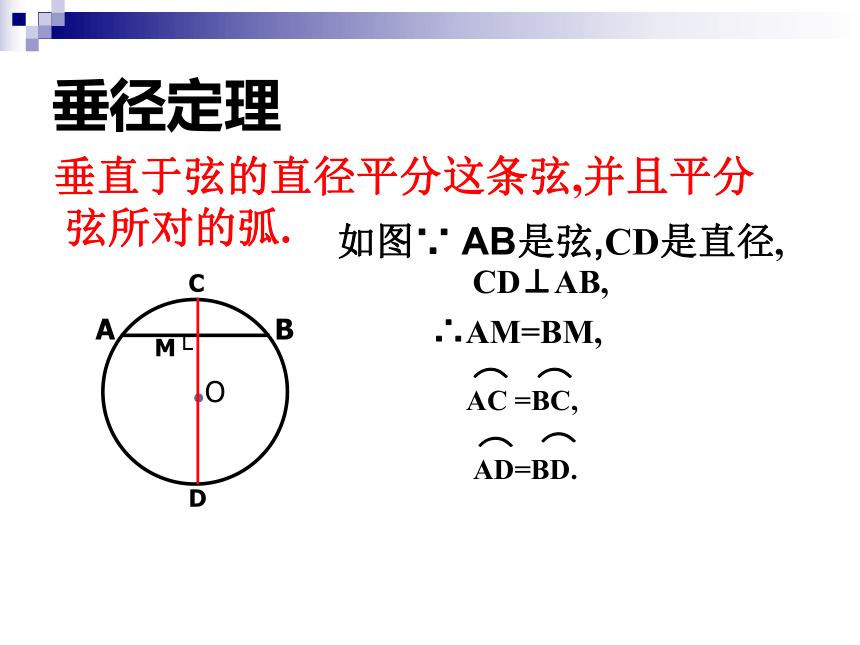
课件25张PPT。§3.2圆的对称性(一)圆是轴对称图形吗?你发现圆的对称轴有什么特点?可用什么方法找到圆的对称轴?小明买了一个圆形的软大饼,小华看见了想要分一半吃,小明能恰好把饼分成相等的两半吗? 你能找到多少条对称轴?利用折叠的方法即可解决上述所有问题.圆的对称性 圆是轴对称图形,其对称轴是任意一条过圆心的直线.
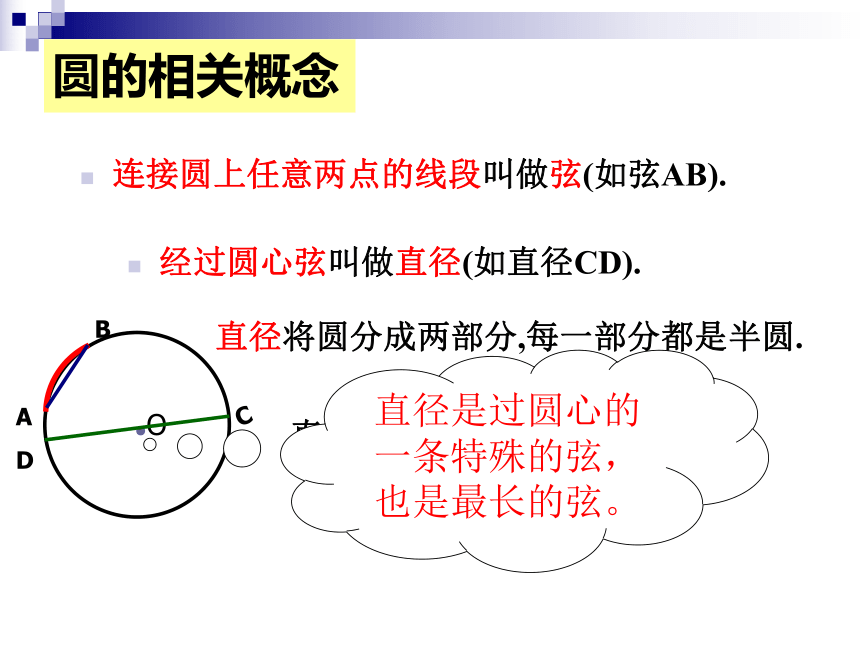
它有无数条对称轴.圆的相关概念圆上任意两点间的部分叫做圆弧,简称弧.弧包括优弧和劣弧 .以A,B为端点的弧有两条,一条是劣弧,另一条是优弧 半圆是弧吗?它是优弧吗?是劣弧吗?我们能说弧是半圆吗?连接圆上任意两点的线段叫做弦(如弦AB).经过圆心弦叫做直径(如直径CD).直径将圆分成两部分,每一部分都是半圆.圆的相关概念直径是弦吗?弦是直径吗? 直径是过圆心的一条特殊的弦,也是最长的弦。判断题1.半圆是弧 ( )
2.弧是半圆 ( )
3.直径是弦 ( )
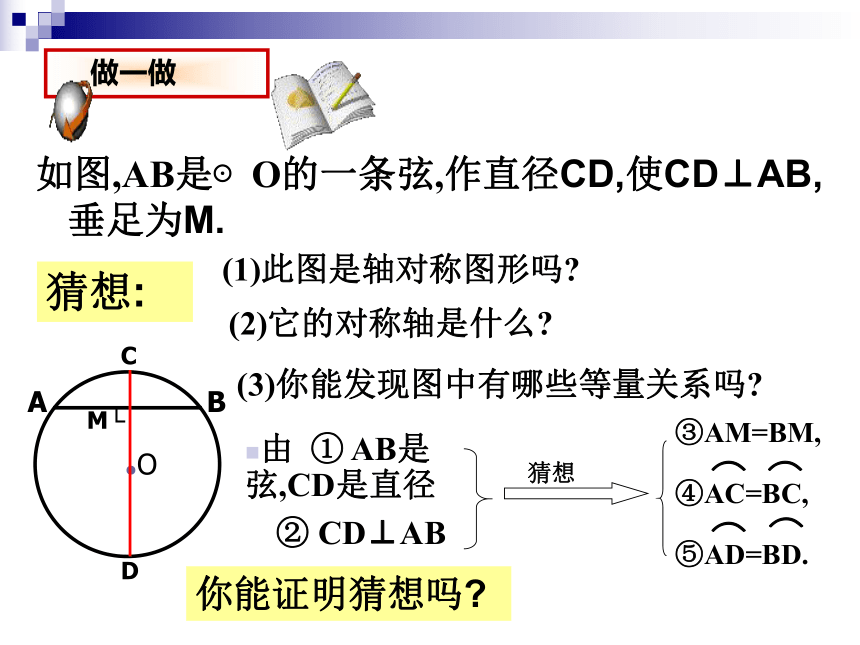
4.弦是直径 ( )③AM=BM,如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.(3)你能发现图中有哪些等量关系吗?(1)此图是轴对称图形吗?由 ① AB是弦,CD是直径② CD⊥AB(2)它的对称轴是什么?猜想:你能证明猜想吗?连接OA,OB,
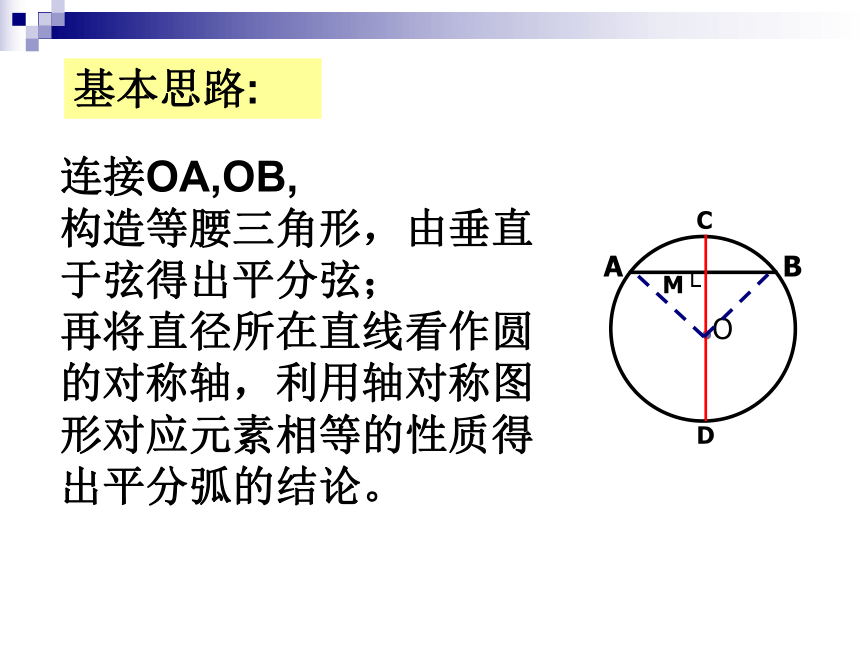
构造等腰三角形,由垂直于弦得出平分弦;
再将直径所在直线看作圆的对称轴,利用轴对称图形对应元素相等的性质得出平分弧的结论。基本思路:垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的弧.CD⊥AB,如图∵ AB是弦,CD是直径,∴AM=BM, 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。E练一练:试 金 石垂径定理三角形在a,d,r,h中,已知其中任意两个量,可以求出其它两个量.⑴d + h = r⑵已知:如图,直径CD⊥AB,垂足为E .
⑴若半径R = 2 ,AB = , 求OE、DE 的长.
⑵若半径R = 2 ,OE = 1 ,求AB、DE 的长.
⑶由⑴ 、⑵两题的启发,你还能编出什么其他问题?垂径定理的应用 如图,一条公路的转弯处是一段圆弧(即图中 ,点O是 的圆心),其中CD=600m,E为 上一点,且OE⊥CD,垂足为F,EF=90 m,求这段弯路的半径。 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE讲解讲解如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?圆的两条平行弦所夹的弧相等小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,⊙O的半径为5cm,思考题:(1)请根据题意画出符合条件的图形(2)求出AB、与CD间的距离。(1)(2)②CD⊥AB, 如图,AB是⊙O的一条弦(不是直径),作一条平分AB的直径CD,交AB于点M由 ① AB是弦(不是直径), CD是直径③ AM=BM(3)你能发现图中有哪些等量关系吗?(1)此图是轴对称图形吗?(2)它的对称轴是什么?猜想:垂径定理的一个逆定理平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.∴CD⊥AB,如图∵ AB是弦(不是直径),CD是直径, AM=BM,如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① AB是弦,CD是直径,③ AM=BM,② CD⊥AB,如果你感兴趣可课后试一试垂径定理不止一个逆定理随堂练习1、习题1、2、练一练:试一试:如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.AB(1)圆的轴对称性
(2)与圆有关概念:弧、弦、直径及表示
(3)垂径定理及它的一个逆定理
(4)在应用中圆心到弦的垂线段,弦长的一半,圆的半径,由这三个量所构成的直角三角形是解决有关圆的问题的一个重要的基本图形。请谈谈本节课的收获?课堂小结:挑战自我判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )见作业本再见
它有无数条对称轴.圆的相关概念圆上任意两点间的部分叫做圆弧,简称弧.弧包括优弧和劣弧 .以A,B为端点的弧有两条,一条是劣弧,另一条是优弧 半圆是弧吗?它是优弧吗?是劣弧吗?我们能说弧是半圆吗?连接圆上任意两点的线段叫做弦(如弦AB).经过圆心弦叫做直径(如直径CD).直径将圆分成两部分,每一部分都是半圆.圆的相关概念直径是弦吗?弦是直径吗? 直径是过圆心的一条特殊的弦,也是最长的弦。判断题1.半圆是弧 ( )
2.弧是半圆 ( )
3.直径是弦 ( )
4.弦是直径 ( )③AM=BM,如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.(3)你能发现图中有哪些等量关系吗?(1)此图是轴对称图形吗?由 ① AB是弦,CD是直径② CD⊥AB(2)它的对称轴是什么?猜想:你能证明猜想吗?连接OA,OB,
构造等腰三角形,由垂直于弦得出平分弦;
再将直径所在直线看作圆的对称轴,利用轴对称图形对应元素相等的性质得出平分弧的结论。基本思路:垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的弧.CD⊥AB,如图∵ AB是弦,CD是直径,∴AM=BM, 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。E练一练:试 金 石垂径定理三角形在a,d,r,h中,已知其中任意两个量,可以求出其它两个量.⑴d + h = r⑵已知:如图,直径CD⊥AB,垂足为E .
⑴若半径R = 2 ,AB = , 求OE、DE 的长.
⑵若半径R = 2 ,OE = 1 ,求AB、DE 的长.
⑶由⑴ 、⑵两题的启发,你还能编出什么其他问题?垂径定理的应用 如图,一条公路的转弯处是一段圆弧(即图中 ,点O是 的圆心),其中CD=600m,E为 上一点,且OE⊥CD,垂足为F,EF=90 m,求这段弯路的半径。 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE讲解讲解如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?圆的两条平行弦所夹的弧相等小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,⊙O的半径为5cm,思考题:(1)请根据题意画出符合条件的图形(2)求出AB、与CD间的距离。(1)(2)②CD⊥AB, 如图,AB是⊙O的一条弦(不是直径),作一条平分AB的直径CD,交AB于点M由 ① AB是弦(不是直径), CD是直径③ AM=BM(3)你能发现图中有哪些等量关系吗?(1)此图是轴对称图形吗?(2)它的对称轴是什么?猜想:垂径定理的一个逆定理平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.∴CD⊥AB,如图∵ AB是弦(不是直径),CD是直径, AM=BM,如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① AB是弦,CD是直径,③ AM=BM,② CD⊥AB,如果你感兴趣可课后试一试垂径定理不止一个逆定理随堂练习1、习题1、2、练一练:试一试:如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.AB(1)圆的轴对称性
(2)与圆有关概念:弧、弦、直径及表示
(3)垂径定理及它的一个逆定理
(4)在应用中圆心到弦的垂线段,弦长的一半,圆的半径,由这三个量所构成的直角三角形是解决有关圆的问题的一个重要的基本图形。请谈谈本节课的收获?课堂小结:挑战自我判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )见作业本再见
