2021-2022学年高二上学期数学人教A版选修2-12.2.1椭圆及其标准方程课件(23张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版选修2-12.2.1椭圆及其标准方程课件(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 454.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 09:40:16 | ||
图片预览








文档简介
(共23张PPT)
椭圆及其标准方程-2
当堂检测:
1.两焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离之和等于10,求椭圆的标准方程
2.焦点F1(-4,0),F2(4,0)的椭圆的一条弦AB
过点F1,且△ABF2周长为20,求椭圆的标准方程
3.a+c=10,a-c=4,求椭圆的标准方程.
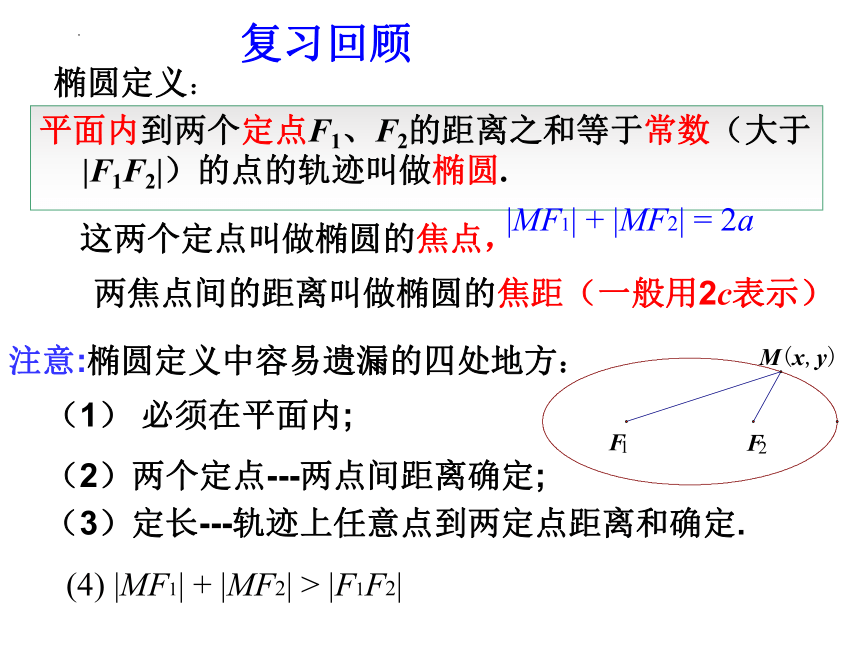
平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点,
椭圆定义:
注意:椭圆定义中容易遗漏的四处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;
(3)定长---轨迹上任意点到两定点距离和确定.
两焦点间的距离叫做椭圆的焦距(一般用2c表示)
(4) |MF1| + |MF2| > |F1F2|
M(x,y)
F
2
F
1
复习回顾
|MF1| + |MF2| = 2a
x
y
F1
F2
P
O
分母哪个大,焦点就在哪个轴上
标准方程
焦点位置的判断
图 形
焦点坐标
a、b、c 的关系
x
y
F1
F2
P
O
椭圆标准方程的统一式
复 习 回 顾
(a>b>0,且c2=a2-b2)
焦点在 x 轴上
(
)
焦点在 y 轴上
(
)
1.若|MF1|+ |MF2|=2a(2a是常数)
2.标准方程
求椭圆标准方程的方法:
----------待定系数法.
当2a>|F1F2|时,点M的轨迹是________;
当2a=|F1F2|时,点M的轨迹是________;
当2a<|F1F2|时,点M的轨迹是________.
椭圆
线段F1F2
不存在
求椭圆标准方程的步骤:
(1)确定焦点位置,设椭圆的标准方程
(2)求a,b(常建立方程 组)(3) 下结论
椭圆的定义与椭圆的标准方程
例1求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,且经过点(2,0)和点(0,1).
(2)经过点(2,0)和点(0,3).
(3)
题型一 求椭圆的标准方程
例1求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,且经过点(2,0)和点(0,1).
(2)经过点(2,0)和点(0,3).
(3)
解:(1)设所求椭圆的标准方程为
待定系数法求椭圆标准方程的解题步骤:
(1)确定焦点的位置(定位)
(2)设出椭圆的标准方程;
(3)用待定系数法确定a、b的值,
写出椭圆的标准方程.
定量
则有
则所求椭圆的标准方程为
题型一 求椭圆的标准方程
例1求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,且经过点(2,0)和点(0,1).
(2)经过点(2,0)和点(0,3).
(3)
解:(1)所求椭圆的标准方程为
(2)设所求椭圆的标准方程为
则所求椭圆的标准方程为
椭圆标准方程的统一式
例1 (3)已知椭圆经过两点 ,
求椭圆的标准方程
(3)解:设椭圆的标准方程
则有
解得
所以,所求椭圆的标准方程为
椭圆标准方程的统一式
例1 (3)已知椭圆经过两点 ,
求椭圆的标准方程
(3)解:设椭圆的标准方程
所以,所求椭圆的标准方程为
椭圆标准方程的统一式:
题型二
椭圆定义的应用
题型二
椭圆定义的应用
C
F1
F2
C
x
y
O
A
B
例2 如图,在圆x2+y2=4上任意一点P,过点P作x轴的垂线段 PD ,D为垂足.当点P在圆上运动时,线段 PD中点M的轨迹是什么?为什么?
解:设 M(x,y),P(x0,y0),则
x
y
.
P
.
M
O
∵ P(x0,y0) 在圆 x2 + y2 = 4 上,
∴ x02 + y02 = 4
得 x2 +4 y2 = 4
∴ 点M的轨迹是一个椭圆 .
D
题型三
椭圆的其他生成方法及其求轨迹方程的代入法
题型四
椭圆标准方程的简单应用
B
题型五
与椭圆有关的轨迹问题
题型五
与椭圆有关的轨迹问题
例5. 求与圆(x+3)2+y2=4外切,且与圆 (x-3)2+y2=100内切的动圆圆心的轨迹方程.
y
x
O1
O2
P
M
Q
O
[分析]充分利用平面几何知识,结合椭圆定义,得到P的轨迹是椭圆.
例5. 求与圆(x+3)2+y2=4外切,且与圆 (x-3)2+y2=100内切的动圆圆心的轨迹方程.
y
x
O1
O2
P
M
Q
O
设动圆的圆心为M(x, y),半径为r,它与已知圆O1、O2切于Q、P 两点,则:
故动圆圆心的轨迹方程为:
变式训练
F1
F2
A
O
x
y
B
解:
(1)由题意
故△AF1B的周长为:
课堂小结:
1.椭圆的定义
2.椭圆的标准方程的求法:
定义和待定系数法
3.轨迹方程的方法:相关点、直接法、
定义法
《作业本》P73-74
椭圆及其标准方程-2
当堂检测:
1.两焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离之和等于10,求椭圆的标准方程
2.焦点F1(-4,0),F2(4,0)的椭圆的一条弦AB
过点F1,且△ABF2周长为20,求椭圆的标准方程
3.a+c=10,a-c=4,求椭圆的标准方程.
平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点,
椭圆定义:
注意:椭圆定义中容易遗漏的四处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;
(3)定长---轨迹上任意点到两定点距离和确定.
两焦点间的距离叫做椭圆的焦距(一般用2c表示)
(4) |MF1| + |MF2| > |F1F2|
M(x,y)
F
2
F
1
复习回顾
|MF1| + |MF2| = 2a
x
y
F1
F2
P
O
分母哪个大,焦点就在哪个轴上
标准方程
焦点位置的判断
图 形
焦点坐标
a、b、c 的关系
x
y
F1
F2
P
O
椭圆标准方程的统一式
复 习 回 顾
(a>b>0,且c2=a2-b2)
焦点在 x 轴上
(
)
焦点在 y 轴上
(
)
1.若|MF1|+ |MF2|=2a(2a是常数)
2.标准方程
求椭圆标准方程的方法:
----------待定系数法.
当2a>|F1F2|时,点M的轨迹是________;
当2a=|F1F2|时,点M的轨迹是________;
当2a<|F1F2|时,点M的轨迹是________.
椭圆
线段F1F2
不存在
求椭圆标准方程的步骤:
(1)确定焦点位置,设椭圆的标准方程
(2)求a,b(常建立方程 组)(3) 下结论
椭圆的定义与椭圆的标准方程
例1求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,且经过点(2,0)和点(0,1).
(2)经过点(2,0)和点(0,3).
(3)
题型一 求椭圆的标准方程
例1求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,且经过点(2,0)和点(0,1).
(2)经过点(2,0)和点(0,3).
(3)
解:(1)设所求椭圆的标准方程为
待定系数法求椭圆标准方程的解题步骤:
(1)确定焦点的位置(定位)
(2)设出椭圆的标准方程;
(3)用待定系数法确定a、b的值,
写出椭圆的标准方程.
定量
则有
则所求椭圆的标准方程为
题型一 求椭圆的标准方程
例1求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,且经过点(2,0)和点(0,1).
(2)经过点(2,0)和点(0,3).
(3)
解:(1)所求椭圆的标准方程为
(2)设所求椭圆的标准方程为
则所求椭圆的标准方程为
椭圆标准方程的统一式
例1 (3)已知椭圆经过两点 ,
求椭圆的标准方程
(3)解:设椭圆的标准方程
则有
解得
所以,所求椭圆的标准方程为
椭圆标准方程的统一式
例1 (3)已知椭圆经过两点 ,
求椭圆的标准方程
(3)解:设椭圆的标准方程
所以,所求椭圆的标准方程为
椭圆标准方程的统一式:
题型二
椭圆定义的应用
题型二
椭圆定义的应用
C
F1
F2
C
x
y
O
A
B
例2 如图,在圆x2+y2=4上任意一点P,过点P作x轴的垂线段 PD ,D为垂足.当点P在圆上运动时,线段 PD中点M的轨迹是什么?为什么?
解:设 M(x,y),P(x0,y0),则
x
y
.
P
.
M
O
∵ P(x0,y0) 在圆 x2 + y2 = 4 上,
∴ x02 + y02 = 4
得 x2 +4 y2 = 4
∴ 点M的轨迹是一个椭圆 .
D
题型三
椭圆的其他生成方法及其求轨迹方程的代入法
题型四
椭圆标准方程的简单应用
B
题型五
与椭圆有关的轨迹问题
题型五
与椭圆有关的轨迹问题
例5. 求与圆(x+3)2+y2=4外切,且与圆 (x-3)2+y2=100内切的动圆圆心的轨迹方程.
y
x
O1
O2
P
M
Q
O
[分析]充分利用平面几何知识,结合椭圆定义,得到P的轨迹是椭圆.
例5. 求与圆(x+3)2+y2=4外切,且与圆 (x-3)2+y2=100内切的动圆圆心的轨迹方程.
y
x
O1
O2
P
M
Q
O
设动圆的圆心为M(x, y),半径为r,它与已知圆O1、O2切于Q、P 两点,则:
故动圆圆心的轨迹方程为:
变式训练
F1
F2
A
O
x
y
B
解:
(1)由题意
故△AF1B的周长为:
课堂小结:
1.椭圆的定义
2.椭圆的标准方程的求法:
定义和待定系数法
3.轨迹方程的方法:相关点、直接法、
定义法
《作业本》P73-74
