2022-2023学年高一上学期数学人教A版(2019)必修第一册3.2.1 单调性与最大(小)值讲义-教案
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册3.2.1 单调性与最大(小)值讲义-教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 387.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 10:06:50 | ||
图片预览



文档简介
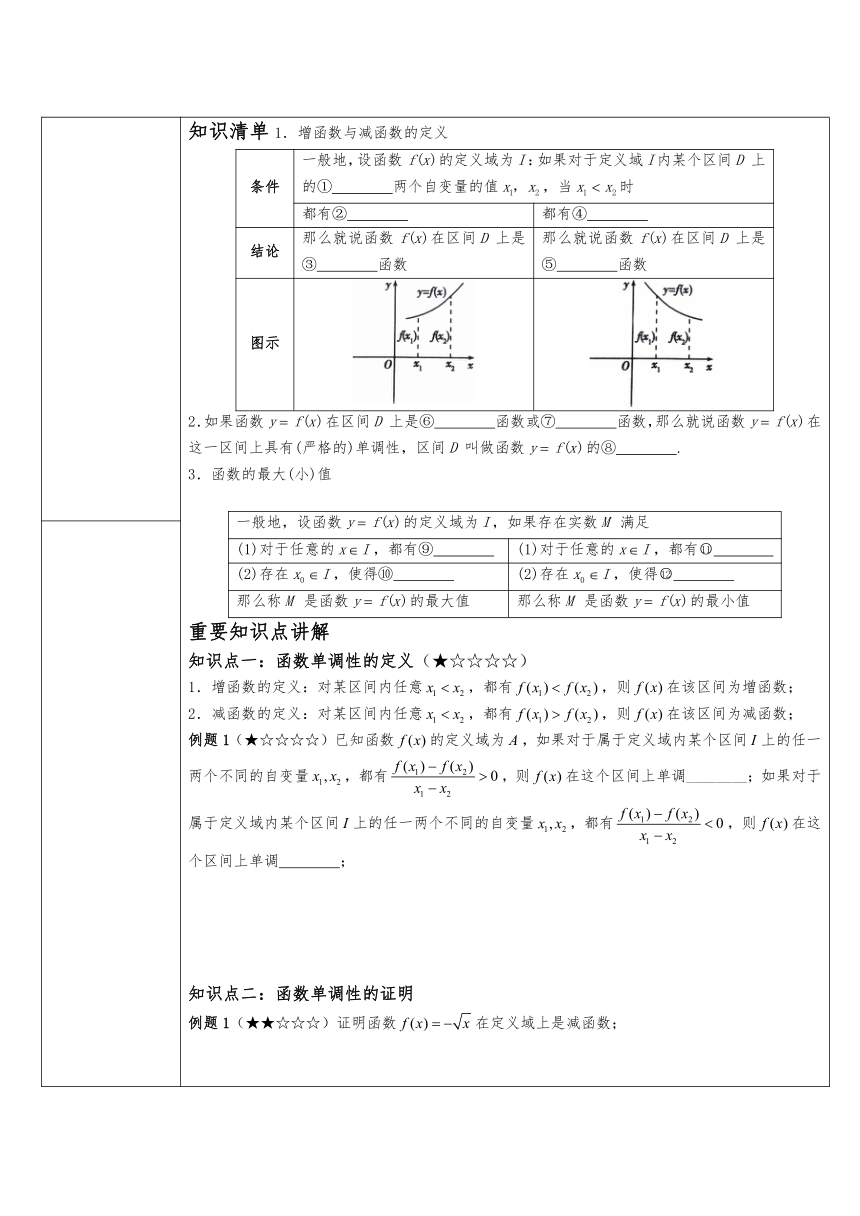
知识清单1.增函数与减函数的定义 条件一般地,设函数的定义域为:如果对于定义域内某个区间上的① 两个自变量的值,当时都有② 都有④ 结论那么就说函数在区间上是③ 函数那么就说函数在区间上是⑤ 函数图示
2.如果函数在区间上是⑥ 函数或⑦ 函数,那么就说函数在这一区间上具有(严格的)单调性,区间叫做函数的⑧ . 3.函数的最大(小)值 一般地,设函数的定义域为,如果存在实数满足(1)对于任意的,都有⑨ (1)对于任意的,都有 (2)存在,使得⑩ (2)存在,使得 那么称是函数的最大值那么称是函数的最小值
重要知识点讲解 知识点一:函数单调性的定义(★☆☆☆☆) 1.增函数的定义:对某区间内任意,都有,则在该区间为增函数; 2.减函数的定义:对某区间内任意,都有,则在该区间为减函数; 例题1(★☆☆☆☆)已知函数的定义域为,如果对于属于定义域内某个区间上的任一两个不同的自变量,都有,则在这个区间上单调________;如果对于属于定义域内某个区间上的任一两个不同的自变量,都有,则在这个区间上单调 ; 知识点二:函数单调性的证明 例题1(★★☆☆☆)证明函数在定义域上是减函数; 变式1(★★☆☆☆)证明函数在上是增函数; 变式2(★★☆☆☆)证明函数在上是减函数; 变式3(★★☆☆☆)证明函数在上是增函数; 变式4(★★☆☆☆)证明函数在上是减函数; 知识点三:函数单调性的判断 解题指导: 1.一次函数,当时,单调递增;当时,单调递减; 2.二次函数对称轴两边单调性恰好相反;当时,对称轴左边单调递减,右边单调递增;当时,对称轴左边单调递增,右边单调递减; 3.反比例,当时,分别在第一、三象限单调递减;当时,分别在第二、四象限单调递增; 4.绝对值函数,图像关于对称,对称轴左边单调递减,右边单调递增; 例题1 (★☆☆☆☆)下列函数在区间上是增函数的是( ) A. B. C. D. 变式1(★☆☆☆☆)下列函数在定义域上单调递减的是( ) A. B. C. D. 知识点四:求单调区间 解题指导: 1.求函数单调性前必须先求定义域,且函数的单调区间必须是定义域的子集; 2.单调区间之间不能用并集符号连接,要用“和”或“,”连接; 例题1(★★★☆☆)先作出下列函数的大致图像,然后根据图像写出其单调区间; (1); (2); (3); 变式1(★★★☆☆)画出函数的图像,并指出函数的单调区间; 例题2(★★★☆☆)函数的单调递增区间是____________; 变式2 (★★★☆☆)函数的单调递增区间是____________; 知识点五:函数单调性的性质 解题指导: 1.如果在某定义域内单调递增,且在该定义域内有,则;如果在某定义域内单调递减,且在该定义域内有,则; 2.函数的单调递增(递减)区间是和函数在上单调递增(递减)是不同的,对于后者,只是其单调递增(递减)区间的子区间; 例题1(★★☆☆☆)已知函数和在上都是减函数,则函数在上是( ) A.减函数且; B.增函数且 ; C.减函数且 ; D.增函数且; 例题2(★★☆☆☆)设函数是上的减函数,则( ) A. B. C. D. 变式1(★★☆☆☆)已知函数是上的减函数,则与的大小关系是 ; 例题3若函数在上是单调函数,则的取值范围是_________; 变式2(★★☆☆☆)已知函数在上递减,在上递增,则 ; 变式3(★★☆☆☆)已知函数,若它的增区间为,则的值是 ;若它在上递增,则的取值范围是_________; 例题4(★★☆☆☆))若函数的单调递增区间是,则______________; 变式4函数在上为增函数,则实数的取值范围是___________; 例题5 (★★★☆☆)已知函数为区间上的增函数,则满足的实数的取值范围是 __________; 变式5(★★★☆☆)已知是定义在上的增函数,且,则的取值范围是__________; 知识点六:复合函数的单调性 解题指导: 1.函数和函数具有相同的单调性; 2.当时,函数和函数具有相同的单调性;当时,函数和函数具有相反的单调性; 3.若,函数和函数有相反的单调性; 4.若,则函数和有相同的单调性; 5.增函数+增函数=增函数;减函数+减函数=减函数;增函数-减函数=增函数;减函数-增函数=减函数; 6.增函数与减函数的复合:增减=减;减增=减;增增=增;减减=增; 记忆方法:可以把增函数当作“正数”,减函数当作“负数”处理。增减函数复合时可以看作乘法运算。 例题1(★☆☆☆☆)函数在上单调_______(填“递增”或“递减”); 变式1(★★☆☆☆)函数在是_______函数(填“增”或“减”); 例题2 (★★★☆☆)函数的单调递增区间是 ; 变式2 (★★☆☆☆)函数的单调递减区间是 ; 知识点七:函数的最值 解题指导:求函数最值的方法 1.观察法:对于简单的函数,可以依据定义域观察求出最值; 2.配方法:对于“二次函数类”的函数,一般通过配方法求最值; 3.图像法:对于图像较为容易画出来的函数,可借助图像直观求出最值; 4.单调性法:对于较复杂的函数,分析单调性(需给出证明)后,依据单调性确定函数最值; (1)如果函数在区间上是增函数,在区间上是减函数,则函数 在处有最大值; (2)如果函数在区间上是减函数,在区间上是增函数,则函数 在处有最小值; (3)若果连续函数在上是单调递增函数,则的最大值是,最小值是; (4)若果连续函数在上是单调递减函数,则的最大值是,最小值是; 例题1 (★★★☆☆)求函数的最小值; 变式1 (★★★☆☆)求函数的最大值与最小值; 重要题型讲解 题型一:带参数的单调性问题 例题1 (★★★★☆)判断函数的单调区间; 变式1 (★★★★☆)求函数的单调区间; 变式2(★★★★☆)试讨论函数在上的单调性; 变式3 (★★★★☆)若函数在上是单调递增函数,则的取值范围是_________; 例题2 (★★★★☆)已知函数在区间上是减函数,则的取值范围是_________; 变式2已知;(1)若,则的定义域为 ;(2)若在区间上是减函数,则实数的取值范围是 ; 题型二:抽象函数的单调性 例题1(★★★★☆)已知函数的定义域为,且对,恒有,且,当时,;求证:是单调递增函数; 变式1已知函数对任意,总有,且当时,,;(1)求证:在上是减函数;(2)在上的最值; 例题2(★★★★☆)当时,函数有意义,且满足条件,是增函数;(1)求证:;(2)若,求的取值范围; 题型三:最值问题 例题1(★★★☆☆)已知函数;(1)当时,求函数的最大值和最小值;(2)求使在区间上是单调函数的实数的范围; 变式1已知函数;(1)当时,求函数的最小值;(2)若对任意,恒成立,试求实数的取值范围; 例题2(★★★☆☆)已知二次函数;(1)当时,求的最值;(2)当时,求的最值;(3)当时,求的最小值; 例题3(★★★★★)求二次函数在时的最大值与最小值; 变式2(★★★★★)求二次函数在时的最大值与最小值;
2.如果函数在区间上是⑥ 函数或⑦ 函数,那么就说函数在这一区间上具有(严格的)单调性,区间叫做函数的⑧ . 3.函数的最大(小)值 一般地,设函数的定义域为,如果存在实数满足(1)对于任意的,都有⑨ (1)对于任意的,都有 (2)存在,使得⑩ (2)存在,使得 那么称是函数的最大值那么称是函数的最小值
重要知识点讲解 知识点一:函数单调性的定义(★☆☆☆☆) 1.增函数的定义:对某区间内任意,都有,则在该区间为增函数; 2.减函数的定义:对某区间内任意,都有,则在该区间为减函数; 例题1(★☆☆☆☆)已知函数的定义域为,如果对于属于定义域内某个区间上的任一两个不同的自变量,都有,则在这个区间上单调________;如果对于属于定义域内某个区间上的任一两个不同的自变量,都有,则在这个区间上单调 ; 知识点二:函数单调性的证明 例题1(★★☆☆☆)证明函数在定义域上是减函数; 变式1(★★☆☆☆)证明函数在上是增函数; 变式2(★★☆☆☆)证明函数在上是减函数; 变式3(★★☆☆☆)证明函数在上是增函数; 变式4(★★☆☆☆)证明函数在上是减函数; 知识点三:函数单调性的判断 解题指导: 1.一次函数,当时,单调递增;当时,单调递减; 2.二次函数对称轴两边单调性恰好相反;当时,对称轴左边单调递减,右边单调递增;当时,对称轴左边单调递增,右边单调递减; 3.反比例,当时,分别在第一、三象限单调递减;当时,分别在第二、四象限单调递增; 4.绝对值函数,图像关于对称,对称轴左边单调递减,右边单调递增; 例题1 (★☆☆☆☆)下列函数在区间上是增函数的是( ) A. B. C. D. 变式1(★☆☆☆☆)下列函数在定义域上单调递减的是( ) A. B. C. D. 知识点四:求单调区间 解题指导: 1.求函数单调性前必须先求定义域,且函数的单调区间必须是定义域的子集; 2.单调区间之间不能用并集符号连接,要用“和”或“,”连接; 例题1(★★★☆☆)先作出下列函数的大致图像,然后根据图像写出其单调区间; (1); (2); (3); 变式1(★★★☆☆)画出函数的图像,并指出函数的单调区间; 例题2(★★★☆☆)函数的单调递增区间是____________; 变式2 (★★★☆☆)函数的单调递增区间是____________; 知识点五:函数单调性的性质 解题指导: 1.如果在某定义域内单调递增,且在该定义域内有,则;如果在某定义域内单调递减,且在该定义域内有,则; 2.函数的单调递增(递减)区间是和函数在上单调递增(递减)是不同的,对于后者,只是其单调递增(递减)区间的子区间; 例题1(★★☆☆☆)已知函数和在上都是减函数,则函数在上是( ) A.减函数且; B.增函数且 ; C.减函数且 ; D.增函数且; 例题2(★★☆☆☆)设函数是上的减函数,则( ) A. B. C. D. 变式1(★★☆☆☆)已知函数是上的减函数,则与的大小关系是 ; 例题3若函数在上是单调函数,则的取值范围是_________; 变式2(★★☆☆☆)已知函数在上递减,在上递增,则 ; 变式3(★★☆☆☆)已知函数,若它的增区间为,则的值是 ;若它在上递增,则的取值范围是_________; 例题4(★★☆☆☆))若函数的单调递增区间是,则______________; 变式4函数在上为增函数,则实数的取值范围是___________; 例题5 (★★★☆☆)已知函数为区间上的增函数,则满足的实数的取值范围是 __________; 变式5(★★★☆☆)已知是定义在上的增函数,且,则的取值范围是__________; 知识点六:复合函数的单调性 解题指导: 1.函数和函数具有相同的单调性; 2.当时,函数和函数具有相同的单调性;当时,函数和函数具有相反的单调性; 3.若,函数和函数有相反的单调性; 4.若,则函数和有相同的单调性; 5.增函数+增函数=增函数;减函数+减函数=减函数;增函数-减函数=增函数;减函数-增函数=减函数; 6.增函数与减函数的复合:增减=减;减增=减;增增=增;减减=增; 记忆方法:可以把增函数当作“正数”,减函数当作“负数”处理。增减函数复合时可以看作乘法运算。 例题1(★☆☆☆☆)函数在上单调_______(填“递增”或“递减”); 变式1(★★☆☆☆)函数在是_______函数(填“增”或“减”); 例题2 (★★★☆☆)函数的单调递增区间是 ; 变式2 (★★☆☆☆)函数的单调递减区间是 ; 知识点七:函数的最值 解题指导:求函数最值的方法 1.观察法:对于简单的函数,可以依据定义域观察求出最值; 2.配方法:对于“二次函数类”的函数,一般通过配方法求最值; 3.图像法:对于图像较为容易画出来的函数,可借助图像直观求出最值; 4.单调性法:对于较复杂的函数,分析单调性(需给出证明)后,依据单调性确定函数最值; (1)如果函数在区间上是增函数,在区间上是减函数,则函数 在处有最大值; (2)如果函数在区间上是减函数,在区间上是增函数,则函数 在处有最小值; (3)若果连续函数在上是单调递增函数,则的最大值是,最小值是; (4)若果连续函数在上是单调递减函数,则的最大值是,最小值是; 例题1 (★★★☆☆)求函数的最小值; 变式1 (★★★☆☆)求函数的最大值与最小值; 重要题型讲解 题型一:带参数的单调性问题 例题1 (★★★★☆)判断函数的单调区间; 变式1 (★★★★☆)求函数的单调区间; 变式2(★★★★☆)试讨论函数在上的单调性; 变式3 (★★★★☆)若函数在上是单调递增函数,则的取值范围是_________; 例题2 (★★★★☆)已知函数在区间上是减函数,则的取值范围是_________; 变式2已知;(1)若,则的定义域为 ;(2)若在区间上是减函数,则实数的取值范围是 ; 题型二:抽象函数的单调性 例题1(★★★★☆)已知函数的定义域为,且对,恒有,且,当时,;求证:是单调递增函数; 变式1已知函数对任意,总有,且当时,,;(1)求证:在上是减函数;(2)在上的最值; 例题2(★★★★☆)当时,函数有意义,且满足条件,是增函数;(1)求证:;(2)若,求的取值范围; 题型三:最值问题 例题1(★★★☆☆)已知函数;(1)当时,求函数的最大值和最小值;(2)求使在区间上是单调函数的实数的范围; 变式1已知函数;(1)当时,求函数的最小值;(2)若对任意,恒成立,试求实数的取值范围; 例题2(★★★☆☆)已知二次函数;(1)当时,求的最值;(2)当时,求的最值;(3)当时,求的最小值; 例题3(★★★★★)求二次函数在时的最大值与最小值; 变式2(★★★★★)求二次函数在时的最大值与最小值;
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
