圆的对称性(1)[下学期]
图片预览



文档简介
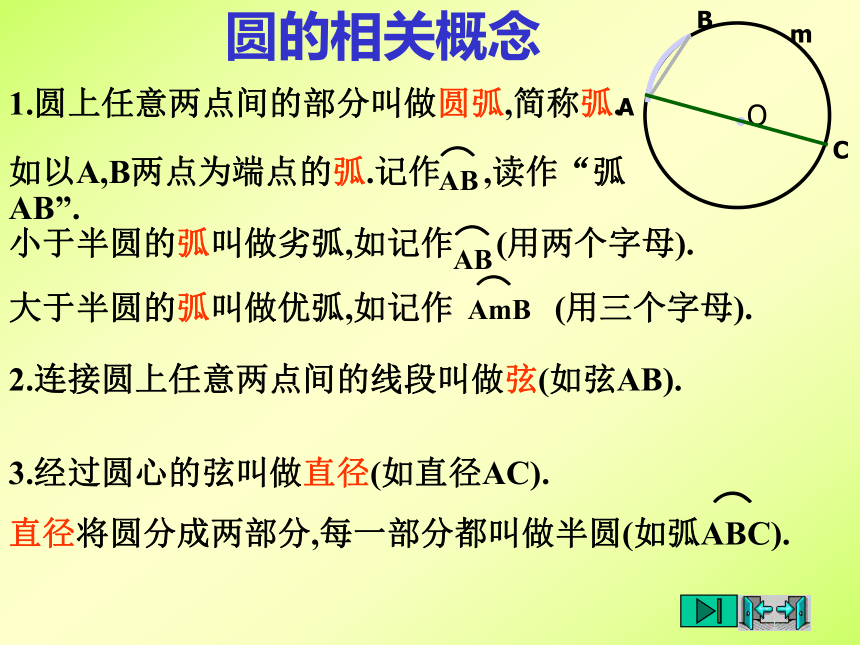
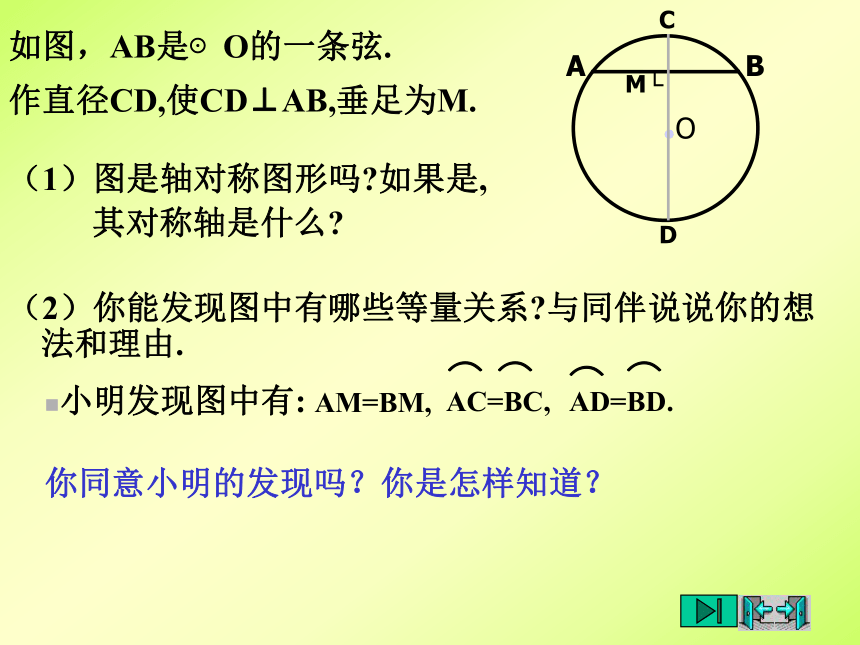
课件10张PPT。2. 圆对称性(1)垂径定理(1)圆是轴对称图形吗?(2)如果是,它的对称轴是什么?你能找到多少条对称轴?圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.圆的相关概念1.圆上任意两点间的部分叫做圆弧,简称弧.直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).2.连接圆上任意两点间的线段叫做弦(如弦AB).3.经过圆心的弦叫做直径(如直径AC).⌒如图,AB是⊙O的一条弦.(2)你能发现图中有哪些等量关系?与同伴说说你的想法和理由.作直径CD,使CD⊥AB,垂足为M.(1)图是轴对称图形吗?如果是,
其对称轴是什么?你同意小明的发现吗?你是怎样知道?如图,小明的理由是:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM,∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,垂径定理定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.老师提示:
垂径定理是圆中一个重要的结论,是计算线段长度的重要根据.CD⊥AB,如图∵ CD是直径,∴AM=BM,③AM=BM,由 ① CD是直径② CD⊥AB②CD⊥AB,垂径定理的推论AB是⊙O的一条弦,且AM=BM.(2)你能发现图中有哪些等量关系?与同伴说说你的想法和理由.过点M作直径CD.(1)右图是轴对称图形吗?如果是,
其对称轴是什么?小明发现:由 ① CD是直径③ AM=BM平分弦(不是直径)的直径垂直于这弦,并且平 分弦所对的两条弧.┗垂径定理的推论如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,③AM=BM, ① CD是直径② CD⊥AB由 ① CD是直径③ AM=BM②CD⊥AB,1.已知:如图,⊙O 中, AB为 弦,OC ⊥ AB交AB于D,交AB于C, ⊙O 的半径为5cm ,OD = 3cm ,求弦AB的长.
挑战自我⌒2.如果圆的两条弦互相平行,那么这两条弦所平的弧相等吗?老师提示: 这两条弦在圆中位置有两种情况:垂径定理的推论 圆的两条平行弦所夹的弧相等.
其对称轴是什么?你同意小明的发现吗?你是怎样知道?如图,小明的理由是:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM,∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,垂径定理定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.老师提示:
垂径定理是圆中一个重要的结论,是计算线段长度的重要根据.CD⊥AB,如图∵ CD是直径,∴AM=BM,③AM=BM,由 ① CD是直径② CD⊥AB②CD⊥AB,垂径定理的推论AB是⊙O的一条弦,且AM=BM.(2)你能发现图中有哪些等量关系?与同伴说说你的想法和理由.过点M作直径CD.(1)右图是轴对称图形吗?如果是,
其对称轴是什么?小明发现:由 ① CD是直径③ AM=BM平分弦(不是直径)的直径垂直于这弦,并且平 分弦所对的两条弧.┗垂径定理的推论如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,③AM=BM, ① CD是直径② CD⊥AB由 ① CD是直径③ AM=BM②CD⊥AB,1.已知:如图,⊙O 中, AB为 弦,OC ⊥ AB交AB于D,交AB于C, ⊙O 的半径为5cm ,OD = 3cm ,求弦AB的长.
挑战自我⌒2.如果圆的两条弦互相平行,那么这两条弦所平的弧相等吗?老师提示: 这两条弦在圆中位置有两种情况:垂径定理的推论 圆的两条平行弦所夹的弧相等.
