圆的对称性(第2课时)[下学期]
图片预览



文档简介
课件27张PPT。§3.2圆的对称性(二)1、已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,⊙O的半径_____。
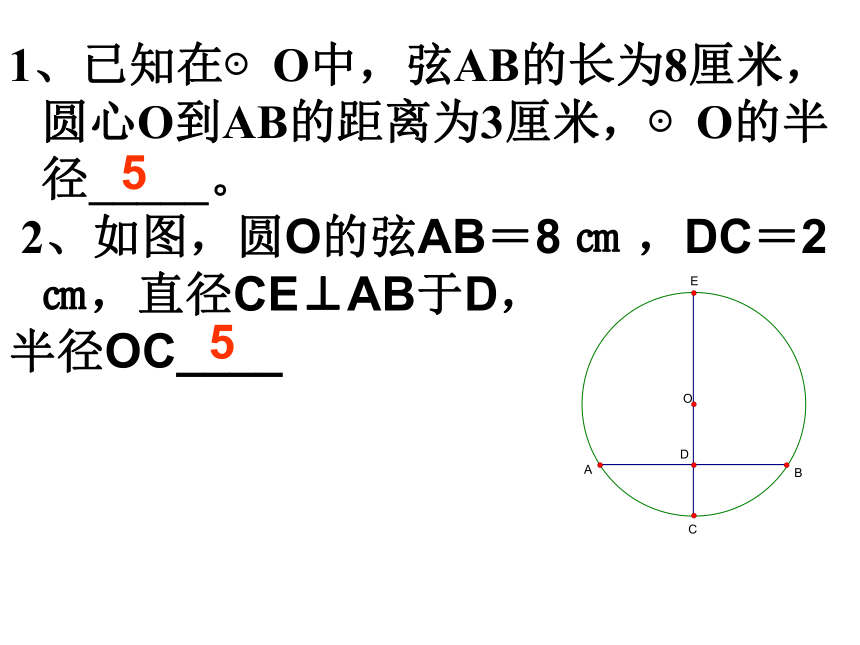
2、如图,圆O的弦AB=8 ㎝ ,DC=2㎝,直径CE⊥AB于D,
半径OC____553:在半径为50㎜的圆O中,有长50㎜的
弦AB,(1)点O与AB的距离为_____
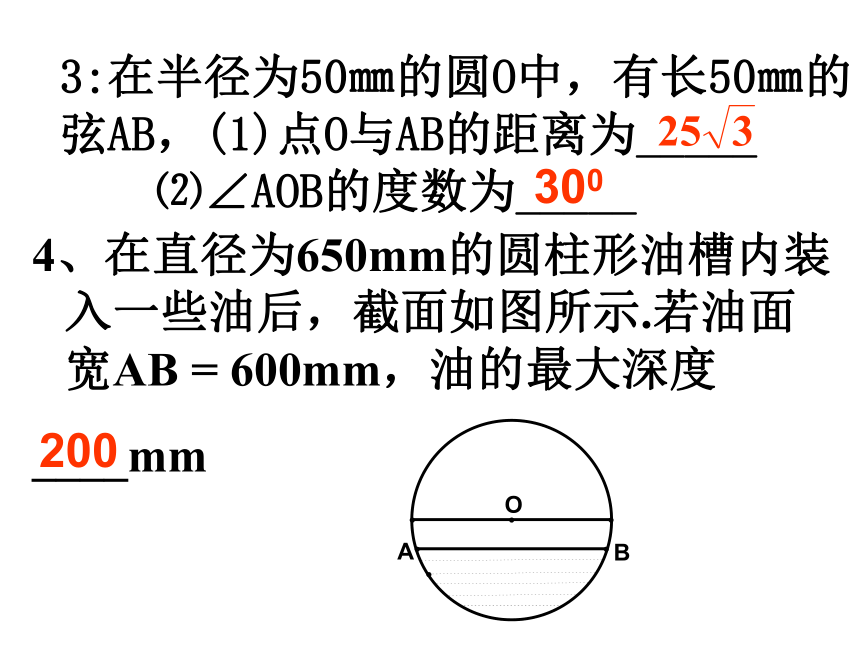
⑵∠AOB的度数为_____3004、在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,油的最大深度
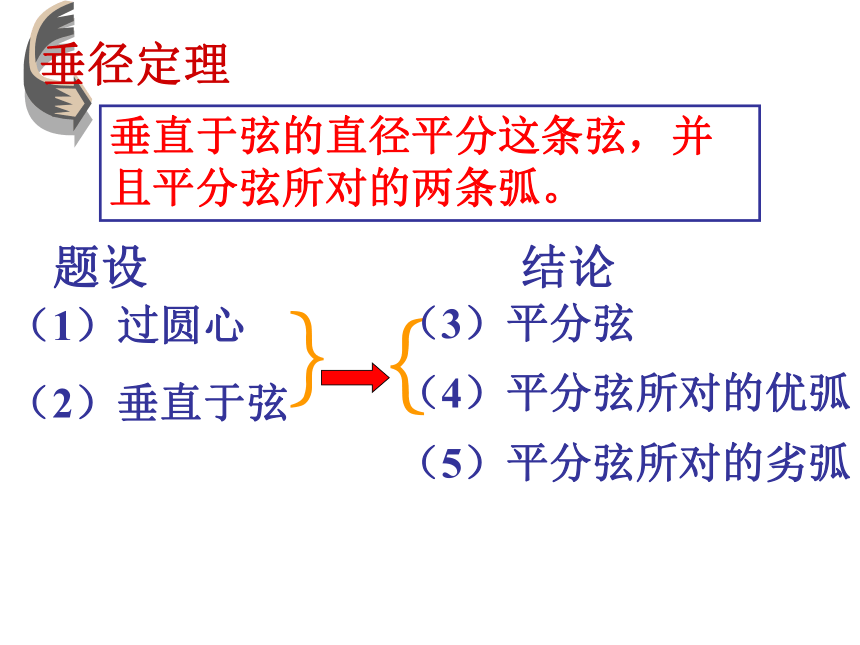
____mm200垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。题设结论(1)过圆心
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
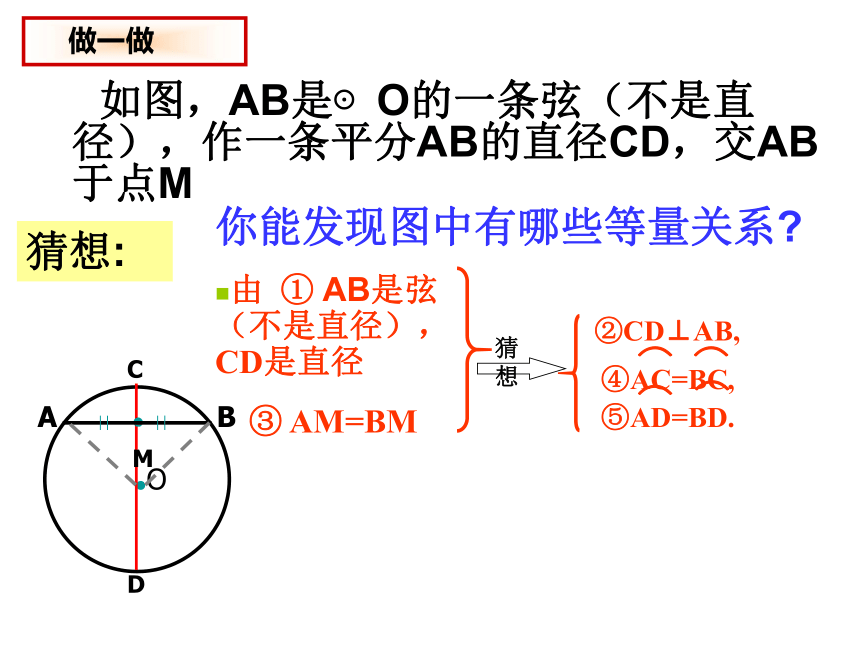
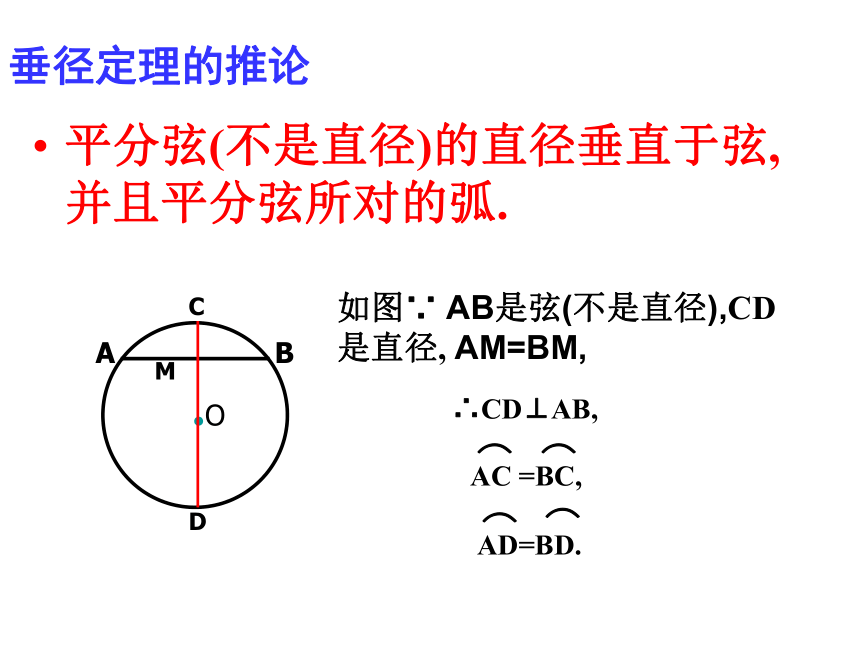
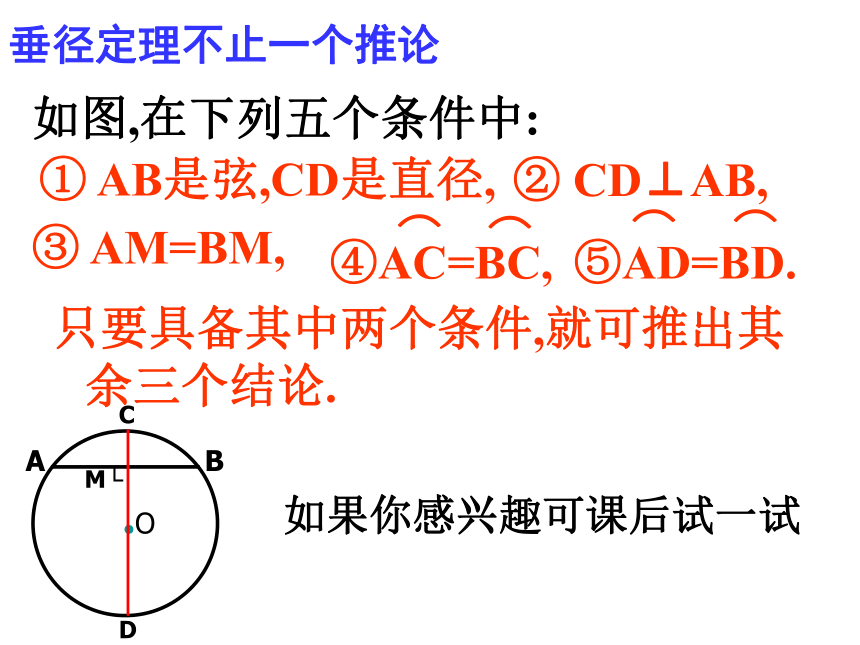
(5)平分弦所对的劣弧②CD⊥AB, 如图,AB是⊙O的一条弦(不是直径),作一条平分AB的直径CD,交AB于点M由 ① AB是弦(不是直径), CD是直径③ AM=BM你能发现图中有哪些等量关系?猜想:垂径定理的推论平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.∴CD⊥AB,如图∵ AB是弦(不是直径),CD是直径, AM=BM,如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① AB是弦,CD是直径,③ AM=BM,② CD⊥AB,如果你感兴趣可课后试一试垂径定理不止一个推论推论(1)(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对和的另一条弧根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备(1)过圆心 (2)垂直于弦
(3)平分弦(4)平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论注意 已知:⊙O中弦AB∥CD。
求证:AC=BD⌒⌒如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?垂径定理的推论2 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等老师提示: 这两条弦在圆中位置有两种情况:判断:
1、垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
2、平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( ) 3、圆的两条弦所夹的弧相等,则这两条弦平行. ( )
4、弦的垂直平分线一定平分这条弦所对的弧. ( )×√√×5、弦所对的两弧中点的连线,垂直于弦,并且经过圆心 ( )6、圆的不与直径垂直的弦必不被这条直径平分 ( )7、平分弦的直径垂直于弦,并且平分弦所对的两条弧 ( )8、圆内两条非直径的弦不能互相平分( )√××√垂径定理的应用 例2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。 已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,⊙O的半径为5cm,思考题:(1)请根据题意画出符合条件的图形(2)求出AB、与CD间的距离。学生练习已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF例3:如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
练习:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。(1)圆的轴对称性
(2)垂径定理及它的推论
(3)在应用中圆心到弦的垂线段,弦长的一半,圆的半径,由这三个量所构成的直角三角形是解决有关圆的问题的一个重要的基本图形。请谈谈本节课的收获?课堂小结:小 结1、圆的轴对称性
2、垂径定理及其推论
再见船能过拱桥吗2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?相信自己能独立完成解答.船能过拱桥吗解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得在Rt△OAD中,由勾股定理,得解得 R≈3.9(m).在Rt△ONH中,由勾股定理,得∴此货船能顺利通过这座拱桥.赵州石拱桥1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).你是第一个告诉同学们解题方法和结果的吗?赵州石拱桥解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.
2、如图,圆O的弦AB=8 ㎝ ,DC=2㎝,直径CE⊥AB于D,
半径OC____553:在半径为50㎜的圆O中,有长50㎜的
弦AB,(1)点O与AB的距离为_____
⑵∠AOB的度数为_____3004、在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,油的最大深度
____mm200垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。题设结论(1)过圆心
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧②CD⊥AB, 如图,AB是⊙O的一条弦(不是直径),作一条平分AB的直径CD,交AB于点M由 ① AB是弦(不是直径), CD是直径③ AM=BM你能发现图中有哪些等量关系?猜想:垂径定理的推论平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.∴CD⊥AB,如图∵ AB是弦(不是直径),CD是直径, AM=BM,如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① AB是弦,CD是直径,③ AM=BM,② CD⊥AB,如果你感兴趣可课后试一试垂径定理不止一个推论推论(1)(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对和的另一条弧根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备(1)过圆心 (2)垂直于弦
(3)平分弦(4)平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论注意 已知:⊙O中弦AB∥CD。
求证:AC=BD⌒⌒如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?垂径定理的推论2 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等老师提示: 这两条弦在圆中位置有两种情况:判断:
1、垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
2、平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( ) 3、圆的两条弦所夹的弧相等,则这两条弦平行. ( )
4、弦的垂直平分线一定平分这条弦所对的弧. ( )×√√×5、弦所对的两弧中点的连线,垂直于弦,并且经过圆心 ( )6、圆的不与直径垂直的弦必不被这条直径平分 ( )7、平分弦的直径垂直于弦,并且平分弦所对的两条弧 ( )8、圆内两条非直径的弦不能互相平分( )√××√垂径定理的应用 例2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。 已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,⊙O的半径为5cm,思考题:(1)请根据题意画出符合条件的图形(2)求出AB、与CD间的距离。学生练习已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF例3:如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
练习:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。(1)圆的轴对称性
(2)垂径定理及它的推论
(3)在应用中圆心到弦的垂线段,弦长的一半,圆的半径,由这三个量所构成的直角三角形是解决有关圆的问题的一个重要的基本图形。请谈谈本节课的收获?课堂小结:小 结1、圆的轴对称性
2、垂径定理及其推论
再见船能过拱桥吗2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?相信自己能独立完成解答.船能过拱桥吗解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得在Rt△OAD中,由勾股定理,得解得 R≈3.9(m).在Rt△ONH中,由勾股定理,得∴此货船能顺利通过这座拱桥.赵州石拱桥1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).你是第一个告诉同学们解题方法和结果的吗?赵州石拱桥解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.
