2021-2022学年北师大版七年级数学下册4.1.4认识三角形(4) 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册4.1.4认识三角形(4) 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 595.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 11:03:42 | ||
图片预览




文档简介
(共20张PPT)
4.1.4认识三角形(4)
第四章 认识三角形
复习回顾
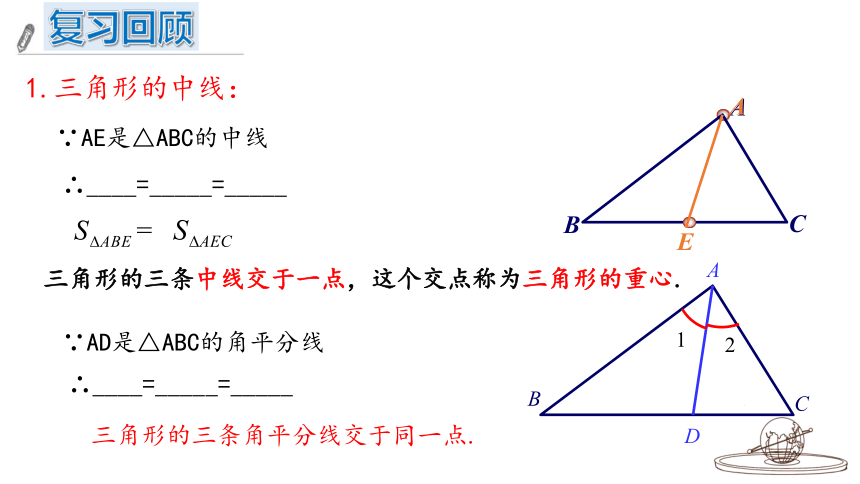
1.三角形的中线:
B
A
C
A
E
∵AE是△ABC的中线
∴____=_____=_____
1
2
A
∵AD是△ABC的角平分线
∴____=_____=_____
D
B
C
三角形的三条角平分线交于同一点.
三角形的三条中线交于一点,这个交点称为三角形的重心.
A
B
C
A
B
C
A
B
C
复习回顾
热身:做三角形的中线和平分线
新知探究
A
B
C
D
和垂足的字母.
注意
!
标明垂直的记号
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
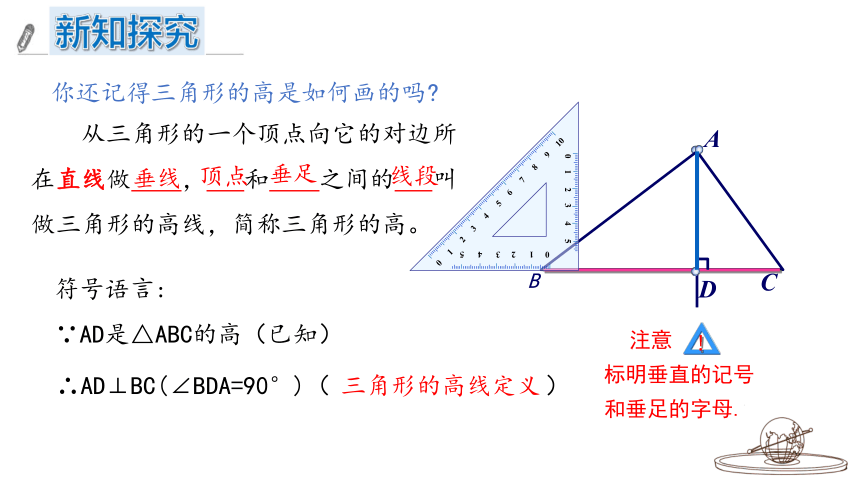
从三角形的一个顶点向它的对边所在直线做 , 和 之间的 叫做三角形的高线,简称三角形的高。
符号语言:
∵AD是△ABC的高(已知)
∴AD⊥BC(∠BDA=90°)( )
垂线
顶点
垂足
线段
三角形的高线定义
你还记得三角形的高是如何画的吗
二、新知探究
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
(3) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
锐角三角形的三条高
如图所示;
二、新知探究
直角边BC边上的高是 ;
直角边AB边上的高是 ;
AC边上的高是 ;
直角三角形的三条高
A
B
C
AB
BC
D
直角三角形的三条高交于直角顶点.
BD
二、新知探究
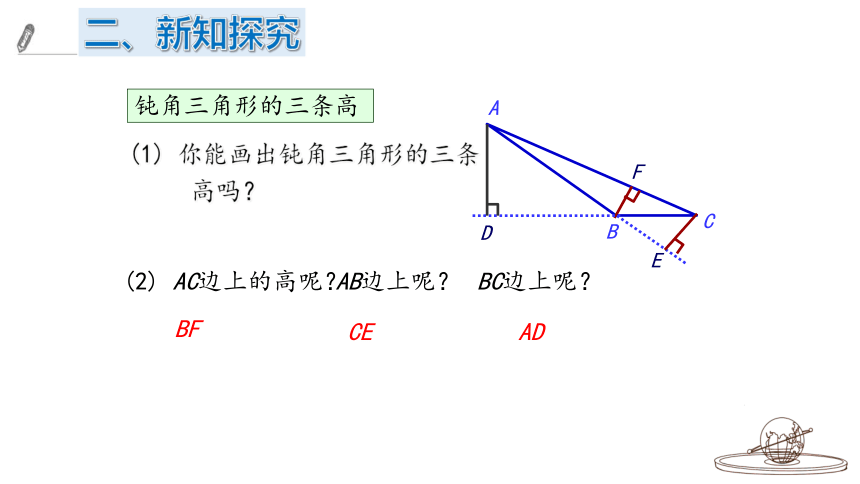
钝角三角形的三条高
(1) 你能画出钝角三角形的三条
高吗?
A
B
C
D
E
F
(2) AC边上的高呢?
AB边上呢?
BC边上呢?
BF
CE
AD
二、新知探究
A
B
C
D
F
(3)钝角三角形的三条高
交于一点吗?
(4)它们所在的直线交于
一点吗?
O
E
钝角三角形的三条高
不相交于一点;
钝角三角形的三条高所在直线交于一点.
三角形的三条高所在直线交于一点.
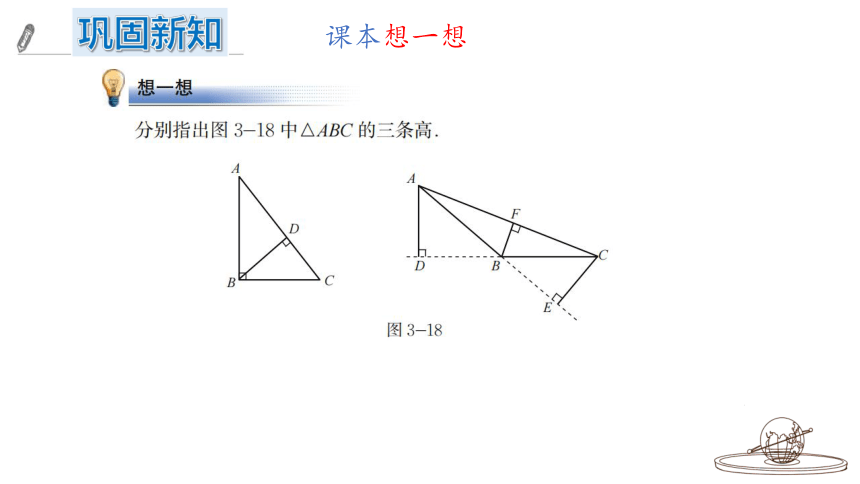
巩固新知
课本想一想
典例精讲
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
课本90页,随堂练习
典例精讲
课本91页,知识技能
C
A
B
E
H
1
D
2
例1 如图,△ABC中,BD、CE分别是边AC、AB上的高,BD、CE交于点H.
(1)若∠A=45°,求∠BHC的度数?.
典例精讲
(2)探究∠1与 ∠2的数量关系?
变式1 在△ABC中,AD是边BC上的高,∠BAD=65°,∠CAD=35°求∠BAC的度数.
典例精讲
C
A
B
E
H
1
D
2
例2 如图,△ABC中,BD、CE分别是边AC、AB上的高,AB=10cm, AC=6cm ,若BD=9cm,求CE的长度?.
典例精讲
变式1 如图,△ABC中,AB=AC=6,D在BC边上,且DE⊥AB,DF⊥AC, △ABC 的面积为24,求DE+DF的值.
典例精讲
C
A
B
E
F
D
思考:如图,等边△ABC中,O在△ABC内,且OE⊥BC,OF⊥AC, OD⊥AB, AM⊥BC,求证:OD + OE + OF=AM.
典例精讲
典例精讲
例2 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
拓展提升
例3 如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.
方法总结:可利用面积相等作桥梁(但不求面积)
求三角形的高,此解题方法通常称为“等面积法”.
拓展提升
课堂小结
三角形的高
锐角三角形的三条高
都在三角形的内部.
高的定义
高的性质
直角三角形的三条高
交于直角顶点.
钝角三角形的三条高
所在直线交于一点.
4.1.4认识三角形(4)
第四章 认识三角形
复习回顾
1.三角形的中线:
B
A
C
A
E
∵AE是△ABC的中线
∴____=_____=_____
1
2
A
∵AD是△ABC的角平分线
∴____=_____=_____
D
B
C
三角形的三条角平分线交于同一点.
三角形的三条中线交于一点,这个交点称为三角形的重心.
A
B
C
A
B
C
A
B
C
复习回顾
热身:做三角形的中线和平分线
新知探究
A
B
C
D
和垂足的字母.
注意
!
标明垂直的记号
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
从三角形的一个顶点向它的对边所在直线做 , 和 之间的 叫做三角形的高线,简称三角形的高。
符号语言:
∵AD是△ABC的高(已知)
∴AD⊥BC(∠BDA=90°)( )
垂线
顶点
垂足
线段
三角形的高线定义
你还记得三角形的高是如何画的吗
二、新知探究
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
(3) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
锐角三角形的三条高
如图所示;
二、新知探究
直角边BC边上的高是 ;
直角边AB边上的高是 ;
AC边上的高是 ;
直角三角形的三条高
A
B
C
AB
BC
D
直角三角形的三条高交于直角顶点.
BD
二、新知探究
钝角三角形的三条高
(1) 你能画出钝角三角形的三条
高吗?
A
B
C
D
E
F
(2) AC边上的高呢?
AB边上呢?
BC边上呢?
BF
CE
AD
二、新知探究
A
B
C
D
F
(3)钝角三角形的三条高
交于一点吗?
(4)它们所在的直线交于
一点吗?
O
E
钝角三角形的三条高
不相交于一点;
钝角三角形的三条高所在直线交于一点.
三角形的三条高所在直线交于一点.
巩固新知
课本想一想
典例精讲
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
课本90页,随堂练习
典例精讲
课本91页,知识技能
C
A
B
E
H
1
D
2
例1 如图,△ABC中,BD、CE分别是边AC、AB上的高,BD、CE交于点H.
(1)若∠A=45°,求∠BHC的度数?.
典例精讲
(2)探究∠1与 ∠2的数量关系?
变式1 在△ABC中,AD是边BC上的高,∠BAD=65°,∠CAD=35°求∠BAC的度数.
典例精讲
C
A
B
E
H
1
D
2
例2 如图,△ABC中,BD、CE分别是边AC、AB上的高,AB=10cm, AC=6cm ,若BD=9cm,求CE的长度?.
典例精讲
变式1 如图,△ABC中,AB=AC=6,D在BC边上,且DE⊥AB,DF⊥AC, △ABC 的面积为24,求DE+DF的值.
典例精讲
C
A
B
E
F
D
思考:如图,等边△ABC中,O在△ABC内,且OE⊥BC,OF⊥AC, OD⊥AB, AM⊥BC,求证:OD + OE + OF=AM.
典例精讲
典例精讲
例2 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
拓展提升
例3 如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.
方法总结:可利用面积相等作桥梁(但不求面积)
求三角形的高,此解题方法通常称为“等面积法”.
拓展提升
课堂小结
三角形的高
锐角三角形的三条高
都在三角形的内部.
高的定义
高的性质
直角三角形的三条高
交于直角顶点.
钝角三角形的三条高
所在直线交于一点.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
