2022-2023学年鲁教版(五四学制)七年级上册数学第三章 勾股定理 全章测试(含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)七年级上册数学第三章 勾股定理 全章测试(含答案) | 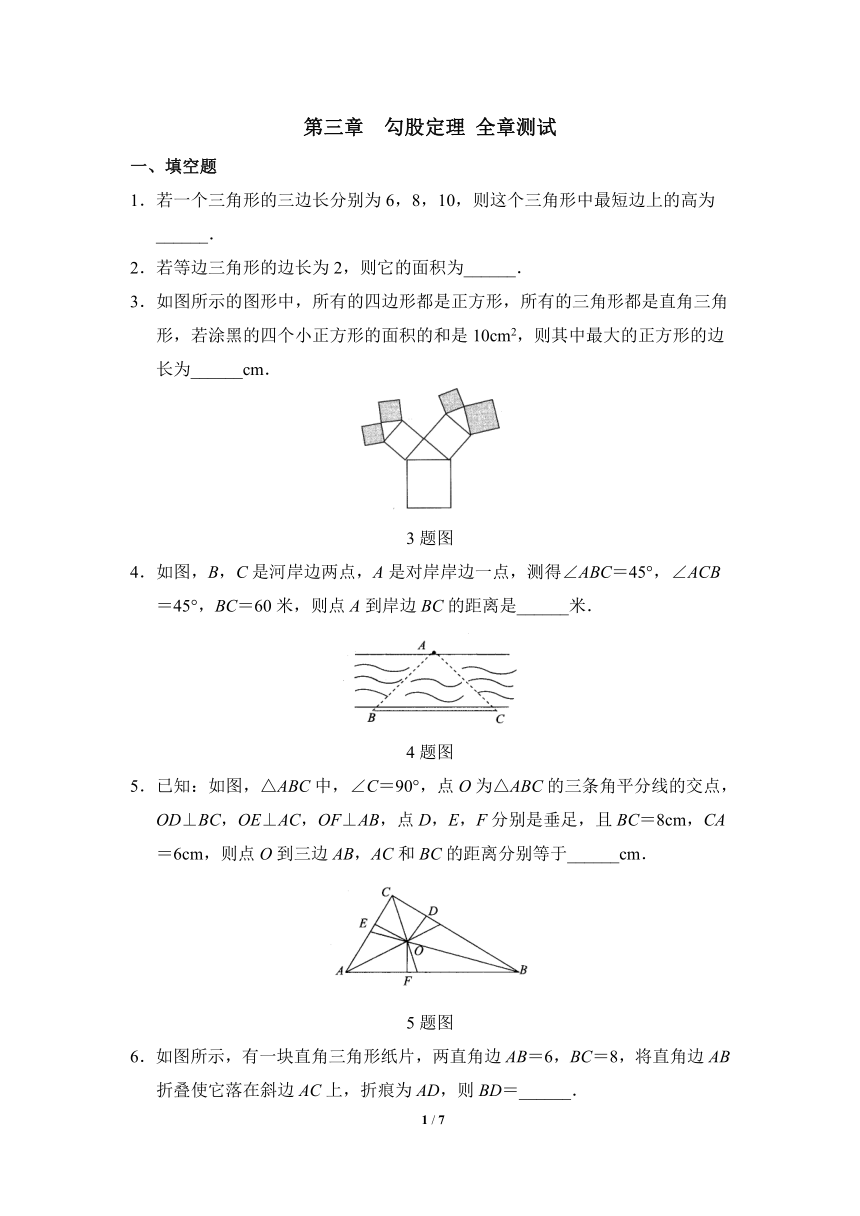 | |
| 格式 | doc | ||
| 文件大小 | 126.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 16:52:58 | ||
图片预览


文档简介
第三章 勾股定理 全章测试
一、填空题
1.若一个三角形的三边长分别为6,8,10,则这个三角形中最短边上的高为______.
2.若等边三角形的边长为2,则它的面积为______.
3.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若涂黑的四个小正方形的面积的和是10cm2,则其中最大的正方形的边长为______cm.
3题图
4.如图,B,C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60米,则点A到岸边BC的距离是______米.
4题图
5.已知:如图,△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F分别是垂足,且BC=8cm,CA=6cm,则点O到三边AB,AC和BC的距离分别等于______cm.
5题图
6.如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将直角边AB折叠使它落在斜边AC上,折痕为AD,则BD=______.
6题图
7.△ABC中,AB=AC=13,若AB边上的高CD=5,则BC=______.
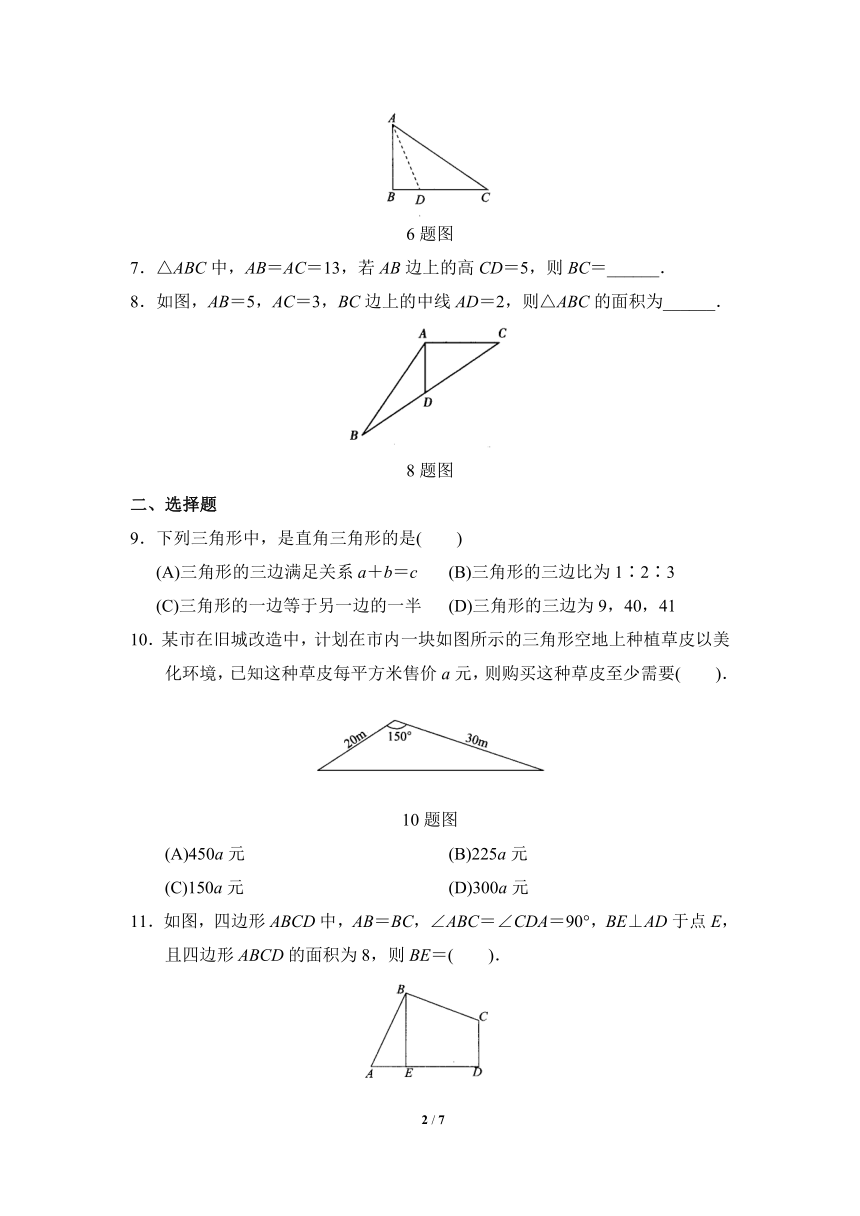
8.如图,AB=5,AC=3,BC边上的中线AD=2,则△ABC的面积为______.
8题图
二、选择题
9.下列三角形中,是直角三角形的是( )
(A)三角形的三边满足关系a+b=c (B)三角形的三边比为1∶2∶3
(C)三角形的一边等于另一边的一半 (D)三角形的三边为9,40,41
10.某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( ).
10题图
(A)450a元 (B)225a元
(C)150a元 (D)300a元
11.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( ).
(A)2 (B)3
(C) (D)
12.如图,Rt△ABC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC等于( ).
(A)5 (B)
(C) (D)
三、解答题
13.已知:如图,△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足,求AD的长.
14.如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
15.△ABC中,AB=AC=4,点P在BC边上运动,猜想AP2+PB·PC的值是否随点P位置的变化而变化,并证明你的猜想.
16.已知:△ABC中,AB=15,AC=13,BC边上的高AD=12,求BC.
17.如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过四个侧面缠绕一圈到达点B,那么所用细线最短需要多长 如果从点A开始经过四个侧面缠绕n圈到达点B,那么所用细线最短需要多长
18.如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长都为3,另一种纸片的两条直角边长分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
图1 图2 图3
(1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹);
(2)三种方法所拼得的平行四边形的面积是否是定值 若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的面积各是多少;
(3)三种方法所拼得的平行四边形的周长是否是定值 若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的周长各是多少.
19.有一块直角三角形的绿地,量得两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
参考答案
1.8. 2. 3. 4.30. 5.2.
6.3.提示:设点B落在AC上的E点处,设BD=x,则DE=BD=x,AE=AB=6,
CE=4,CD=8-x,在Rt△CDE中根据勾股定理列方程.
7.或
8.6.提示:延长AD到E,使DE=AD,连结BE,可得△ABE为Rt△.
9.D. 10.C 11.C. 12.B
13. 提示:作CE⊥AB于E可得由勾股定理得由三角形面积公式计算AD长.
14.150m2.提示:延长BC,AD交于E.
15.提示:过A作AH⊥BC于H
AP2+PB·PC=AH2+PH2+(BH-PH)(CH+PH)
=AH2+PH2+BH2-PH2
=AH2+BH2=AB2=16.
16.14或4.
17.10;
18.(1)略; (2)定值, 12;(3)不是定值,
19.在Rt△ABC中,∠ACB=90°,AC=8,BC=6
由勾股定理得:AB=10,扩充部分为Rt△ACD,扩充成等腰△ABD,应分以下三种情况.
①如图1,当AB=AD=10时,可求CD=CB=6得△ABD的周长为32m.
图1
②如图2,当AB=BD=10时,可求CD=4
图2
由勾股定理得:,得△ABD的周长为.
③如图3,当AB为底时,设AD=BD=x,则CD=x-6,
图3
由勾股定理得:,得△ABD的周长为
7 / 7
一、填空题
1.若一个三角形的三边长分别为6,8,10,则这个三角形中最短边上的高为______.
2.若等边三角形的边长为2,则它的面积为______.
3.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若涂黑的四个小正方形的面积的和是10cm2,则其中最大的正方形的边长为______cm.
3题图
4.如图,B,C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60米,则点A到岸边BC的距离是______米.
4题图
5.已知:如图,△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F分别是垂足,且BC=8cm,CA=6cm,则点O到三边AB,AC和BC的距离分别等于______cm.
5题图
6.如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将直角边AB折叠使它落在斜边AC上,折痕为AD,则BD=______.
6题图
7.△ABC中,AB=AC=13,若AB边上的高CD=5,则BC=______.
8.如图,AB=5,AC=3,BC边上的中线AD=2,则△ABC的面积为______.
8题图
二、选择题
9.下列三角形中,是直角三角形的是( )
(A)三角形的三边满足关系a+b=c (B)三角形的三边比为1∶2∶3
(C)三角形的一边等于另一边的一半 (D)三角形的三边为9,40,41
10.某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( ).
10题图
(A)450a元 (B)225a元
(C)150a元 (D)300a元
11.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( ).
(A)2 (B)3
(C) (D)
12.如图,Rt△ABC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC等于( ).
(A)5 (B)
(C) (D)
三、解答题
13.已知:如图,△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足,求AD的长.
14.如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
15.△ABC中,AB=AC=4,点P在BC边上运动,猜想AP2+PB·PC的值是否随点P位置的变化而变化,并证明你的猜想.
16.已知:△ABC中,AB=15,AC=13,BC边上的高AD=12,求BC.
17.如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过四个侧面缠绕一圈到达点B,那么所用细线最短需要多长 如果从点A开始经过四个侧面缠绕n圈到达点B,那么所用细线最短需要多长
18.如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长都为3,另一种纸片的两条直角边长分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
图1 图2 图3
(1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹);
(2)三种方法所拼得的平行四边形的面积是否是定值 若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的面积各是多少;
(3)三种方法所拼得的平行四边形的周长是否是定值 若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的周长各是多少.
19.有一块直角三角形的绿地,量得两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
参考答案
1.8. 2. 3. 4.30. 5.2.
6.3.提示:设点B落在AC上的E点处,设BD=x,则DE=BD=x,AE=AB=6,
CE=4,CD=8-x,在Rt△CDE中根据勾股定理列方程.
7.或
8.6.提示:延长AD到E,使DE=AD,连结BE,可得△ABE为Rt△.
9.D. 10.C 11.C. 12.B
13. 提示:作CE⊥AB于E可得由勾股定理得由三角形面积公式计算AD长.
14.150m2.提示:延长BC,AD交于E.
15.提示:过A作AH⊥BC于H
AP2+PB·PC=AH2+PH2+(BH-PH)(CH+PH)
=AH2+PH2+BH2-PH2
=AH2+BH2=AB2=16.
16.14或4.
17.10;
18.(1)略; (2)定值, 12;(3)不是定值,
19.在Rt△ABC中,∠ACB=90°,AC=8,BC=6
由勾股定理得:AB=10,扩充部分为Rt△ACD,扩充成等腰△ABD,应分以下三种情况.
①如图1,当AB=AD=10时,可求CD=CB=6得△ABD的周长为32m.
图1
②如图2,当AB=BD=10时,可求CD=4
图2
由勾股定理得:,得△ABD的周长为.
③如图3,当AB为底时,设AD=BD=x,则CD=x-6,
图3
由勾股定理得:,得△ABD的周长为
7 / 7
