2022-2023学年鲁教版(五四学制)七年级上册数学第一章 三角形 1单元测试 (含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)七年级上册数学第一章 三角形 1单元测试 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 177.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 17:02:55 | ||
图片预览



文档简介
第一章 三角形
单元测试
一、选择题
1.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为( )
A.10 B.12 C.14 D.16
2.在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是( )
A.a>2 B.2<a<14 C.7<a<14 D.a<14
3.一个三角形的三个内角中,锐角的个数最少为( )
A.0 B.1 C.2 D.3
4.下面说法错误的是( )
A.三角形的三条角平分线交于一点
B.三角形的三条中线交于一点
C.三角形的三条高交于一点
D.三角形的三条高所在的直线交于一点
5.能将一个三角形分成面积相等的两个三角形的一条线段是( )
A.中线 B.角平分线
C.高线 D.三角形的角平分线
6.如图5—12,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是( )
A.∠1 B.∠2 C.∠B D.∠1、∠2和∠B
7.点P是△ABC内任意一点,则∠APC与∠B的大小关系是( )
A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定
8.已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么( )
A.M>0 B. M=0 C.M<0 D.不能确定
9.周长为P的三角形中,最长边m的取值范围是( )
A. B. C. D.
10.各边长均为整数且三边各不相等的三角形的周长小于13,这样的三角形个数共有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
1.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以________个三角形.
2.在△ABC中,AB=6,AC=10,那么BC边的取值范围是________,周长的取值范围是___________.
3.一个三角形的三个内角的度数的比是2:2:1,这个三角形是_________三角形.
4.一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________.
5.在△ABC中,三边长分别为正整数a、b、c,且c≥b≥a>0,如果b=4,则这样的三角形共有_________个.
6.直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________.
7.在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=________.
8.如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是△ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高.
[
9.如图5—14,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____.
10.如图5—15,△ABC中,∠A=60°,∠ABC、∠ACB的平分线BD、CD交于点D,则∠BDC=_____.
11.如图5—16,该五角星中,∠A+∠B+∠C+∠D+∠E=________度.
12.等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是________.
三、解答题
1.如图5—17,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形 说明理由.
2.如图5—18,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗 说明理由.
3.一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗
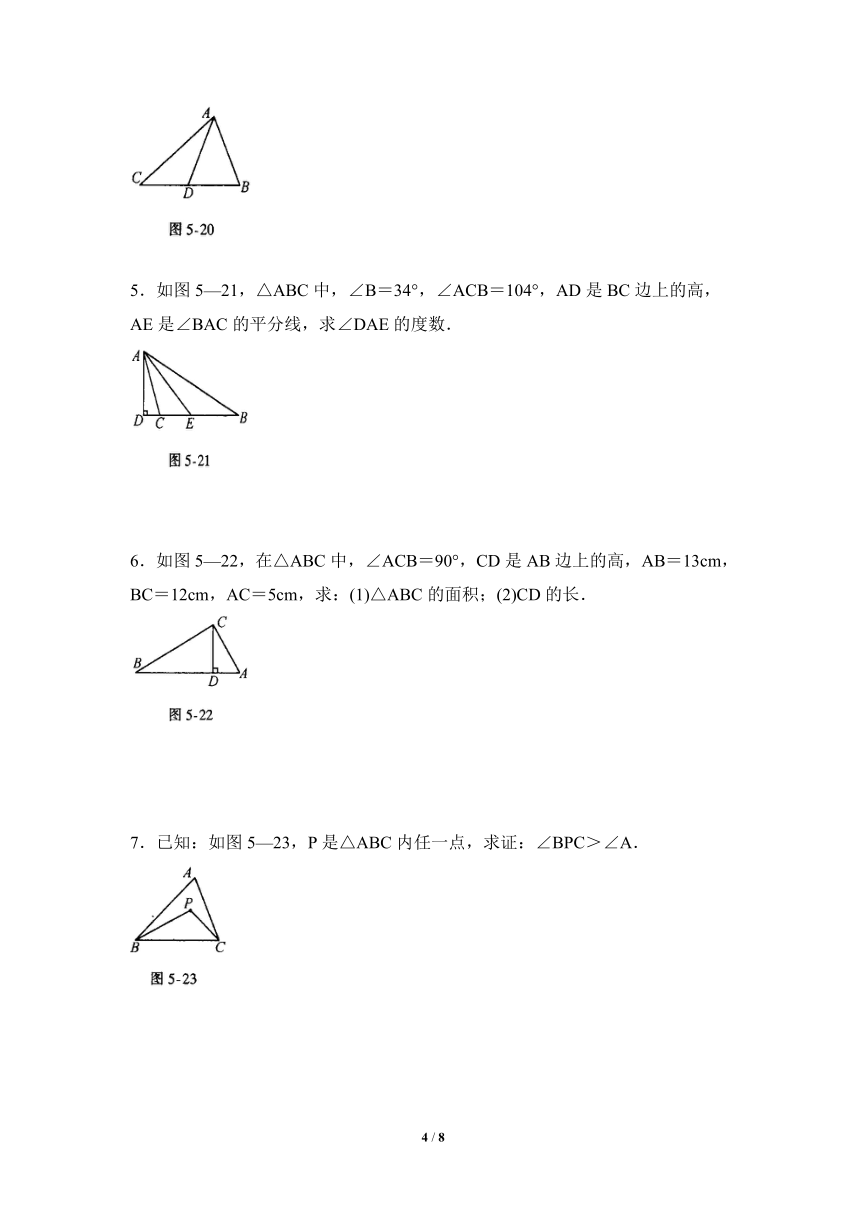
4.如图5—20,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.
5.如图5—21,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
6.如图5—22,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.
7.已知:如图5—23,P是△ABC内任一点,求证:∠BPC>∠A.
8.△ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.
9.已知:如图5—24,P是△ABC内任一点,求证:AB+AC>BP+PC.
10.如图5—25,豫东有四个村庄A、B、C、D.现在要建造一个水塔P.请回答水塔P应建在何位置,才能使它到4村的距离之和最小,说明最节约材料的办法和理由.
参考答案
一、1.C 2.B 3.C 4.C 5.A 6.B 7.A 8.C 9.A 10.C
二、1.3; 2.; 3.锐角(等腰锐角); 4.;5.10; 6.和; 7.; 8.;9.; 10.; 11.; 12..
三、
1.可以确定6个三角形.理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,所以图中可以确定6个三角形.
2.错误.因为AD虽然是线段,但不符合三角形角平分线定义,这里射线AD是的平分线.
3.假设此零件合格,连接BD,则;可知.这与上面的结果不一致,从而知这个零件不合格.
4.∵ AD是BC边上的中线,
∴ D为BC的中点,.
∵ 的周长-的周长=5cm.
∴ .
又∵ ,
∴ .
5.由三角形内角和定理,得
.
∴ .
又∵ AE平分∠BAC.
∴ .
∴ .
又∵ ,
∴ .
6.(1)∵ 在△ABC中,,,,
(2)∵ CD是AB边上的高,
∴.
即.
∴ .
7.如图,延长BP交AC于D,
∵ ,
∴ .
8.∵ ,
∴,
∴ .
又∵ ,
∴ .
∴ ,
∵ ,
∴ .
又∵ 为整数,
∴ ∠C的度数为7的倍数.
∴ ,∴ .
9.如图,延长BP交AC于点D.在△BAD中,,
即:.
在△PDC中,.
①+②得
,
即.
10.如图,水塔P应建在线段AC和线段BD的交点处.这样的设计将最节省材料.
理由:我们不妨任意取一点,连结、、、、、、、,
∵ 在中,, ①
在中,, ②
①+②得.
∵ 点是任意的,代表一般性,
∴ 线段AC和BD的交点处P到4个村的距离之和最小.
8 / 8
单元测试
一、选择题
1.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为( )
A.10 B.12 C.14 D.16
2.在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是( )
A.a>2 B.2<a<14 C.7<a<14 D.a<14
3.一个三角形的三个内角中,锐角的个数最少为( )
A.0 B.1 C.2 D.3
4.下面说法错误的是( )
A.三角形的三条角平分线交于一点
B.三角形的三条中线交于一点
C.三角形的三条高交于一点
D.三角形的三条高所在的直线交于一点
5.能将一个三角形分成面积相等的两个三角形的一条线段是( )
A.中线 B.角平分线
C.高线 D.三角形的角平分线
6.如图5—12,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是( )
A.∠1 B.∠2 C.∠B D.∠1、∠2和∠B
7.点P是△ABC内任意一点,则∠APC与∠B的大小关系是( )
A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定
8.已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么( )
A.M>0 B. M=0 C.M<0 D.不能确定
9.周长为P的三角形中,最长边m的取值范围是( )
A. B. C. D.
10.各边长均为整数且三边各不相等的三角形的周长小于13,这样的三角形个数共有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
1.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以________个三角形.
2.在△ABC中,AB=6,AC=10,那么BC边的取值范围是________,周长的取值范围是___________.
3.一个三角形的三个内角的度数的比是2:2:1,这个三角形是_________三角形.
4.一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________.
5.在△ABC中,三边长分别为正整数a、b、c,且c≥b≥a>0,如果b=4,则这样的三角形共有_________个.
6.直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________.
7.在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=________.
8.如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是△ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高.
[
9.如图5—14,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____.
10.如图5—15,△ABC中,∠A=60°,∠ABC、∠ACB的平分线BD、CD交于点D,则∠BDC=_____.
11.如图5—16,该五角星中,∠A+∠B+∠C+∠D+∠E=________度.
12.等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是________.
三、解答题
1.如图5—17,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形 说明理由.
2.如图5—18,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗 说明理由.
3.一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗
4.如图5—20,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.
5.如图5—21,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
6.如图5—22,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.
7.已知:如图5—23,P是△ABC内任一点,求证:∠BPC>∠A.
8.△ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.
9.已知:如图5—24,P是△ABC内任一点,求证:AB+AC>BP+PC.
10.如图5—25,豫东有四个村庄A、B、C、D.现在要建造一个水塔P.请回答水塔P应建在何位置,才能使它到4村的距离之和最小,说明最节约材料的办法和理由.
参考答案
一、1.C 2.B 3.C 4.C 5.A 6.B 7.A 8.C 9.A 10.C
二、1.3; 2.; 3.锐角(等腰锐角); 4.;5.10; 6.和; 7.; 8.;9.; 10.; 11.; 12..
三、
1.可以确定6个三角形.理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,所以图中可以确定6个三角形.
2.错误.因为AD虽然是线段,但不符合三角形角平分线定义,这里射线AD是的平分线.
3.假设此零件合格,连接BD,则;可知.这与上面的结果不一致,从而知这个零件不合格.
4.∵ AD是BC边上的中线,
∴ D为BC的中点,.
∵ 的周长-的周长=5cm.
∴ .
又∵ ,
∴ .
5.由三角形内角和定理,得
.
∴ .
又∵ AE平分∠BAC.
∴ .
∴ .
又∵ ,
∴ .
6.(1)∵ 在△ABC中,,,,
(2)∵ CD是AB边上的高,
∴.
即.
∴ .
7.如图,延长BP交AC于D,
∵ ,
∴ .
8.∵ ,
∴,
∴ .
又∵ ,
∴ .
∴ ,
∵ ,
∴ .
又∵ 为整数,
∴ ∠C的度数为7的倍数.
∴ ,∴ .
9.如图,延长BP交AC于点D.在△BAD中,,
即:.
在△PDC中,.
①+②得
,
即.
10.如图,水塔P应建在线段AC和线段BD的交点处.这样的设计将最节省材料.
理由:我们不妨任意取一点,连结、、、、、、、,
∵ 在中,, ①
在中,, ②
①+②得.
∵ 点是任意的,代表一般性,
∴ 线段AC和BD的交点处P到4个村的距离之和最小.
8 / 8
