2022-2023学年鲁教版(五四学制)七年级上册数学第一章 三角形(二)综合测评(含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)七年级上册数学第一章 三角形(二)综合测评(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 17:09:46 | ||
图片预览


文档简介
第一章 三角形综合测评(二)
时间: 满分:120分
班级: 姓名: 得分:
一、选择题(每小题4分,共32分)
1. 下列四个图形是全等图形的是( )
A. (1)和(3) B. (2)和(3) C. (2)和(4) D. (3)和(4)
2. 图1中的三角形被木板遮住了一部分,这个三角形是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 以上都有可能
3. 下面的事例:①过去农村的人们通常会在栅栏门上斜着钉上一些木条;②新植的树木,常用一些粗木与之成角度支撑起来防止倒斜;③活动挂衣架;④学校门口的伸缩大门.
其中是用到三角形稳定性的有( )
A.1个 B.2个 C.3个 D.4个
4. 根据下列条件,能画出唯一△ABC的是( )
A.AB=4,BC=5,AC=10 B.AB=5,BC=4,∠A=40°
C.∠A=60°,∠B=50°,AB=5 D.∠C=90°,AB=8
5. 已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A. 2 B. 3 C. 5 D. 13
6. 如图2,要使△ABC≌△ABD,下面给出的四组条件中,错误的一组是( )
A. BC=BD,∠BAC=∠BAD B. ∠C=∠D,∠BAC=∠BAD
C. ∠BAC=∠BAD,∠ABC=∠ABD D. BC=BD,AC=AD
7. 若直角三角形的一个锐角是另一个锐角的4倍,则这个直角三角形中最小锐角的度数是( )
A. 9° B. 18° C. 27° D. 36°
8. 如图3,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:
①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(每小题4分,共32分)
9. 如图4所示,图中有 个三角形, 个直角三角形.
10. 如图5,∠ACD=155°,∠B=35°,则∠A= 度.
11. 如图6所示,CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD的周长差是 cm.
12.已知△DEF≌△ABC,AB=AC,且△ABC的周长为22cm,BC=4cm,则△DEF中最长的一条边为 .
13.如图7,点B、E、C、F在一条直线上,AB∥DE,BE=CF,请添加一个条件 ,使△ABC≌△DEF.
14.如图8是标准跷跷板的示意图.横板AB的中点过支撑点O,且绕点O只能上下转动.如果∠OCA=90°,∠CAO=25°,则小孩玩耍时,跷跷板可以转动的最大角度为 .
15. 已知三角形的两边长分别为3和10,周长恰好是6的倍数,那么第三边长为________.
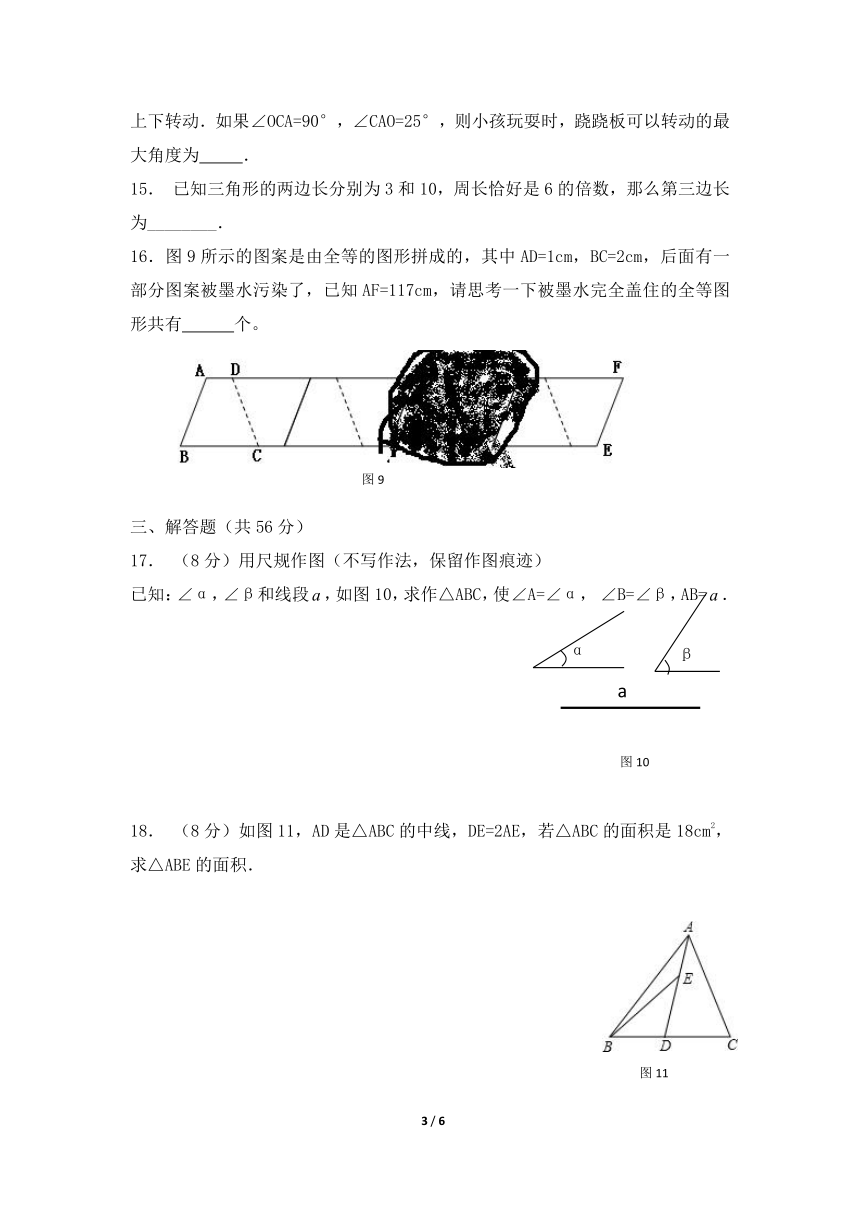
16.图9所示的图案是由全等的图形拼成的,其中AD=1cm,BC=2cm,后面有一部分图案被墨水污染了,已知AF=117cm,请思考一下被墨水完全盖住的全等图形共有 个。
三、解答题(共56分)
17. (8分)用尺规作图(不写作法,保留作图痕迹)
已知:∠α,∠β和线段,如图10,求作△ABC,使∠A=∠α, ∠B=∠β,AB=.
18. (8分)如图11,AD是△ABC的中线,DE=2AE,若△ABC的面积是18cm2,求△ABE的面积.
19. (9分)如图12,AB=AD,AC=AE,∠BAE=∠DAC,试说明∠C=∠E.
20. (10分)如图13,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一颗树A;
②沿河岸直走20步有一树C,继续前行20步到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长就是河宽AB.
请你证明他们做法的正确性.
21. (10分)如图14,已知∠A=∠F,AB∥EF,BC=DE,请说明AD∥CF.
解:因为 BC=DE,
所以 BC+CD=DE+CD,即_________=_________,
又因为AB∥EF(已知),所以 ________=_________.
所以在△ABD与△FEC中,因为∠A=∠F(已知),_______=______,______=______,
所以△ABD≌△FEC(________).
所以∠ADB =∠FCE.
根据“________”,
所以AD∥CF.
22. (11分)以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图15所示放置,使得一直角边重合,连接BD,CE.
(1)说明BD=CE.
(2)延长BD,交CE于点F,求∠BFC的度数.
第一章 三角形综合测评(二)
一、1.C 2.D 3.B 4.C 5.B 6.A 7.B 8.C
二、9. 5 4 10. 120 11. 6 12. 9 cm 13. AB=DE
14. 50° 15. 11 16. 72
三、17.图略.
18. 解:因为AD是△ABC的中线,所以S△ABD=S△ACD.
因为DE=2AE,所以S△ABE=S△DBE,而S△ABE=S△ABC=3cm2.即△ABE的面积是3cm2.
19. 解:因为∠BAE=∠DAC 所以∠BAE+∠EAC =∠DAC+∠EAC,即∠BAC=∠DAE.
所以 在△BAC与△DAE中,AB=AD,∠BAC=∠DAE,AC=AE,所以△BAC≌△DAE(SAS).
所以∠C=∠E.
20. 解:如图,由做法知:
在Rt△ABC和Rt△EDC中,因为∠ABC=∠EDC=90°,BC=DC,∠ACB=∠ECD,所以Rt△ABC≌Rt△EDC.所以AB=ED.
即他们的做法是正确的.
21. 解:空内依次填:BD EC ∠B ∠E ∠B ∠E BD EC 内错角相等,两直线平行
22. 解:(1)因为△ABC、△ADE是等腰直角三角形,所以AB=AC,∠BAD=∠EAC=90°,AD=AE,
所以△ADB≌△AEC(SAS),所以BD=CE.
(2)因为△ADB≌△AEC,所以∠ACE=∠DBA.
而∠BFC=180°∠ACE∠CDF=180°∠DBA ∠BDA=∠DAB=90°.
图1
图3
图2
图6
图4
图5
图1
图8
图7
图9
β
图10
α
a
图11
图12
图13
图14
图15
6 / 6
时间: 满分:120分
班级: 姓名: 得分:
一、选择题(每小题4分,共32分)
1. 下列四个图形是全等图形的是( )
A. (1)和(3) B. (2)和(3) C. (2)和(4) D. (3)和(4)
2. 图1中的三角形被木板遮住了一部分,这个三角形是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 以上都有可能
3. 下面的事例:①过去农村的人们通常会在栅栏门上斜着钉上一些木条;②新植的树木,常用一些粗木与之成角度支撑起来防止倒斜;③活动挂衣架;④学校门口的伸缩大门.
其中是用到三角形稳定性的有( )
A.1个 B.2个 C.3个 D.4个
4. 根据下列条件,能画出唯一△ABC的是( )
A.AB=4,BC=5,AC=10 B.AB=5,BC=4,∠A=40°
C.∠A=60°,∠B=50°,AB=5 D.∠C=90°,AB=8
5. 已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A. 2 B. 3 C. 5 D. 13
6. 如图2,要使△ABC≌△ABD,下面给出的四组条件中,错误的一组是( )
A. BC=BD,∠BAC=∠BAD B. ∠C=∠D,∠BAC=∠BAD
C. ∠BAC=∠BAD,∠ABC=∠ABD D. BC=BD,AC=AD
7. 若直角三角形的一个锐角是另一个锐角的4倍,则这个直角三角形中最小锐角的度数是( )
A. 9° B. 18° C. 27° D. 36°
8. 如图3,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:
①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(每小题4分,共32分)
9. 如图4所示,图中有 个三角形, 个直角三角形.
10. 如图5,∠ACD=155°,∠B=35°,则∠A= 度.
11. 如图6所示,CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD的周长差是 cm.
12.已知△DEF≌△ABC,AB=AC,且△ABC的周长为22cm,BC=4cm,则△DEF中最长的一条边为 .
13.如图7,点B、E、C、F在一条直线上,AB∥DE,BE=CF,请添加一个条件 ,使△ABC≌△DEF.
14.如图8是标准跷跷板的示意图.横板AB的中点过支撑点O,且绕点O只能上下转动.如果∠OCA=90°,∠CAO=25°,则小孩玩耍时,跷跷板可以转动的最大角度为 .
15. 已知三角形的两边长分别为3和10,周长恰好是6的倍数,那么第三边长为________.
16.图9所示的图案是由全等的图形拼成的,其中AD=1cm,BC=2cm,后面有一部分图案被墨水污染了,已知AF=117cm,请思考一下被墨水完全盖住的全等图形共有 个。
三、解答题(共56分)
17. (8分)用尺规作图(不写作法,保留作图痕迹)
已知:∠α,∠β和线段,如图10,求作△ABC,使∠A=∠α, ∠B=∠β,AB=.
18. (8分)如图11,AD是△ABC的中线,DE=2AE,若△ABC的面积是18cm2,求△ABE的面积.
19. (9分)如图12,AB=AD,AC=AE,∠BAE=∠DAC,试说明∠C=∠E.
20. (10分)如图13,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一颗树A;
②沿河岸直走20步有一树C,继续前行20步到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长就是河宽AB.
请你证明他们做法的正确性.
21. (10分)如图14,已知∠A=∠F,AB∥EF,BC=DE,请说明AD∥CF.
解:因为 BC=DE,
所以 BC+CD=DE+CD,即_________=_________,
又因为AB∥EF(已知),所以 ________=_________.
所以在△ABD与△FEC中,因为∠A=∠F(已知),_______=______,______=______,
所以△ABD≌△FEC(________).
所以∠ADB =∠FCE.
根据“________”,
所以AD∥CF.
22. (11分)以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图15所示放置,使得一直角边重合,连接BD,CE.
(1)说明BD=CE.
(2)延长BD,交CE于点F,求∠BFC的度数.
第一章 三角形综合测评(二)
一、1.C 2.D 3.B 4.C 5.B 6.A 7.B 8.C
二、9. 5 4 10. 120 11. 6 12. 9 cm 13. AB=DE
14. 50° 15. 11 16. 72
三、17.图略.
18. 解:因为AD是△ABC的中线,所以S△ABD=S△ACD.
因为DE=2AE,所以S△ABE=S△DBE,而S△ABE=S△ABC=3cm2.即△ABE的面积是3cm2.
19. 解:因为∠BAE=∠DAC 所以∠BAE+∠EAC =∠DAC+∠EAC,即∠BAC=∠DAE.
所以 在△BAC与△DAE中,AB=AD,∠BAC=∠DAE,AC=AE,所以△BAC≌△DAE(SAS).
所以∠C=∠E.
20. 解:如图,由做法知:
在Rt△ABC和Rt△EDC中,因为∠ABC=∠EDC=90°,BC=DC,∠ACB=∠ECD,所以Rt△ABC≌Rt△EDC.所以AB=ED.
即他们的做法是正确的.
21. 解:空内依次填:BD EC ∠B ∠E ∠B ∠E BD EC 内错角相等,两直线平行
22. 解:(1)因为△ABC、△ADE是等腰直角三角形,所以AB=AC,∠BAD=∠EAC=90°,AD=AE,
所以△ADB≌△AEC(SAS),所以BD=CE.
(2)因为△ADB≌△AEC,所以∠ACE=∠DBA.
而∠BFC=180°∠ACE∠CDF=180°∠DBA ∠BDA=∠DAB=90°.
图1
图3
图2
图6
图4
图5
图1
图8
图7
图9
β
图10
α
a
图11
图12
图13
图14
图15
6 / 6
