圆的对称性[下学期]
图片预览


文档简介
课件16张PPT。圆的对称性
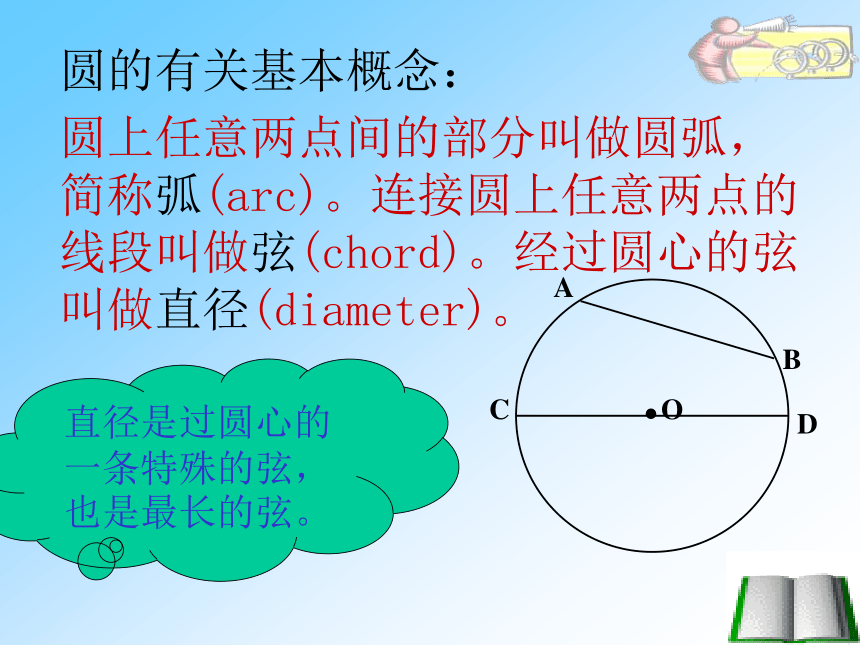
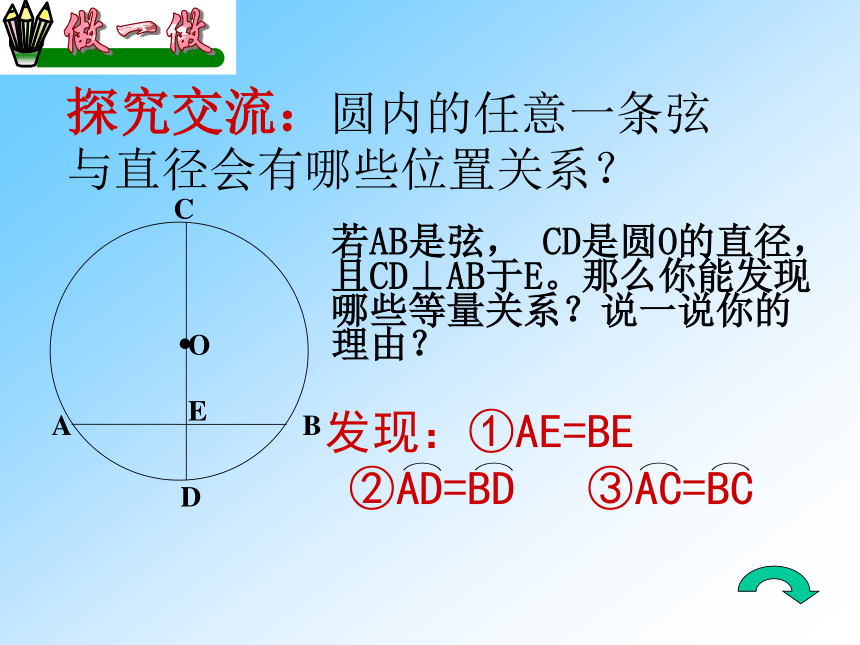
(第一课时)?圆是轴对称图形吗?为什么?圆是轴对称图形,经过圆心的每一条直线都是它们的对称轴。它的对称轴是什么?你能找到多少条对称轴?圆的有关基本概念:圆上任意两点间的部分叫做圆弧,简称弧(arc)。连接圆上任意两点的线段叫做弦(chord)。经过圆心的弦叫做直径(diameter)。直径是过圆心的一条特殊的弦,也是最长的弦。探究交流:圆内的任意一条弦与直径会有哪些位置关系?发现:①AE=BE
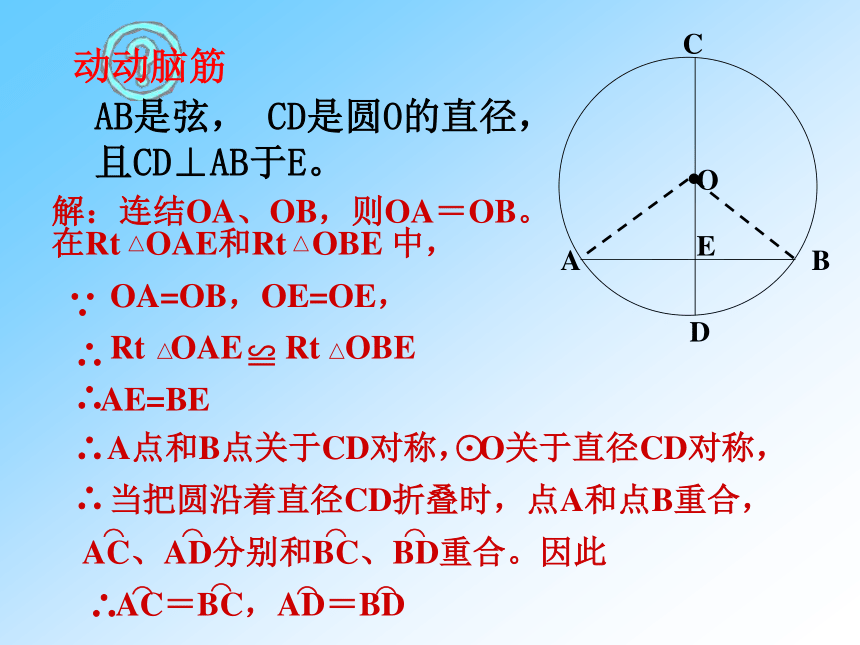
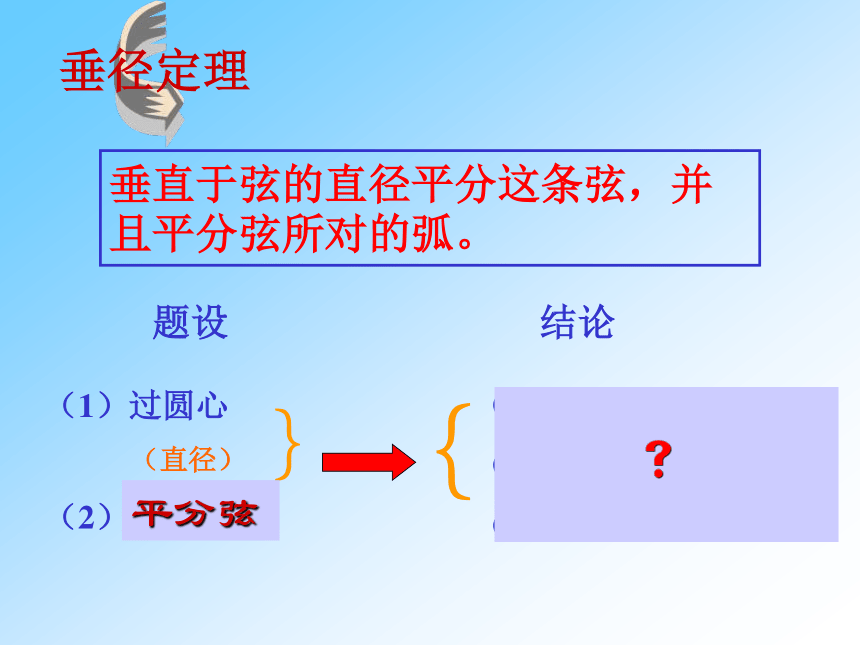
②AD=BD ③AC=BC动动脑筋AB是弦, CD是圆O的直径, 且CD⊥AB于E。垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的弧。题设结论(1)过圆心
(直径)
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧平分弦
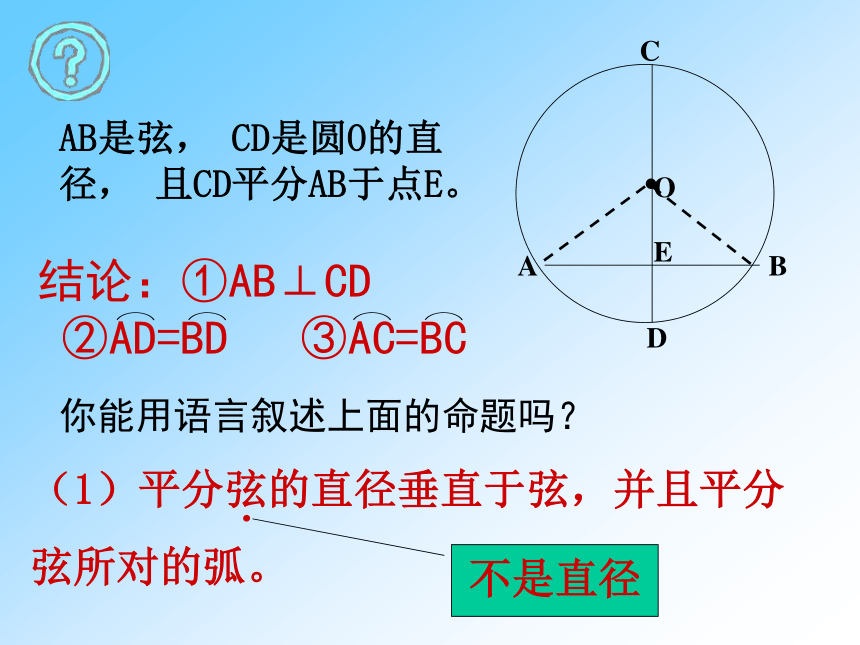
AB是弦, CD是圆O的直径, 且CD平分AB于点E。结论:①AB⊥CD
②AD=BD ③AC=BC(1)平分弦的直径垂直于弦,并且平分
弦所对的弧。
你能用语言叙述上面的命题吗? 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。E练一练:试 金 石讲解 例:如图,一条公路的转弯处是一段圆弧,(即图中CD,点O是CD的圆心),其中CD =600m,E为CD上一点,且OE⊥CD,垂足为F,EF=90m。求这段弯路的半径。
解:连接OC
设弯路的半径为R m,则
OF=(R-90)m
∵OE⊥CD
∴CF=1/2×CD=1/2 ×600 = 300(m)
根据勾股定理, OC2 = CF2 + OF2
即 R2=3002 +(R-90)2
解得 R = 545
所以,这段弯路的半径为545m。 1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度(即弧所对的弦长)为37.4米,拱高(即弧的中点到弦的距离为7.2米,求拱桥所在圆的半径(结果精确到0.1米)。讲解讲解如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?圆的两条平行弦所夹的弧相等 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE讲解小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,
⊙O的半径为5cm,思考题:(1)请根据题意画出符合条件的图形(2)求出AB、与CD间的距离。(1)(2) 利用圆的轴对称性我们学习了垂径定理及其逆定理。想一想,圆除了轴对称性之外还具有什么性质?作业:作业本及试一试
(第一课时)?圆是轴对称图形吗?为什么?圆是轴对称图形,经过圆心的每一条直线都是它们的对称轴。它的对称轴是什么?你能找到多少条对称轴?圆的有关基本概念:圆上任意两点间的部分叫做圆弧,简称弧(arc)。连接圆上任意两点的线段叫做弦(chord)。经过圆心的弦叫做直径(diameter)。直径是过圆心的一条特殊的弦,也是最长的弦。探究交流:圆内的任意一条弦与直径会有哪些位置关系?发现:①AE=BE
②AD=BD ③AC=BC动动脑筋AB是弦, CD是圆O的直径, 且CD⊥AB于E。垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的弧。题设结论(1)过圆心
(直径)
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧平分弦
AB是弦, CD是圆O的直径, 且CD平分AB于点E。结论:①AB⊥CD
②AD=BD ③AC=BC(1)平分弦的直径垂直于弦,并且平分
弦所对的弧。
你能用语言叙述上面的命题吗? 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。E练一练:试 金 石讲解 例:如图,一条公路的转弯处是一段圆弧,(即图中CD,点O是CD的圆心),其中CD =600m,E为CD上一点,且OE⊥CD,垂足为F,EF=90m。求这段弯路的半径。
解:连接OC
设弯路的半径为R m,则
OF=(R-90)m
∵OE⊥CD
∴CF=1/2×CD=1/2 ×600 = 300(m)
根据勾股定理, OC2 = CF2 + OF2
即 R2=3002 +(R-90)2
解得 R = 545
所以,这段弯路的半径为545m。 1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度(即弧所对的弦长)为37.4米,拱高(即弧的中点到弦的距离为7.2米,求拱桥所在圆的半径(结果精确到0.1米)。讲解讲解如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?圆的两条平行弦所夹的弧相等 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE讲解小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,
⊙O的半径为5cm,思考题:(1)请根据题意画出符合条件的图形(2)求出AB、与CD间的距离。(1)(2) 利用圆的轴对称性我们学习了垂径定理及其逆定理。想一想,圆除了轴对称性之外还具有什么性质?作业:作业本及试一试
