3.2圆的对称性(3)[下学期]
图片预览




文档简介
课件18张PPT。 学习目标
1、知道圆是中心对称图形和轴对称图形,并能运用其特有的性质推出在同一个圆中,圆心角、弧、弦之间的关系;
2、能运用圆心角、弧、弦之间的关系解决问题,培养善于从实验中获取知识的科学的方法。
3、在积极参与数学活动的过程中,体验发现问题、总结规律的态度以及养成质疑和独立思考的习惯。圆的对称性(3)1、圆是轴对称图形吗?
2、圆是中心对称图形吗?
3、圆绕着圆心旋转任意角度,是
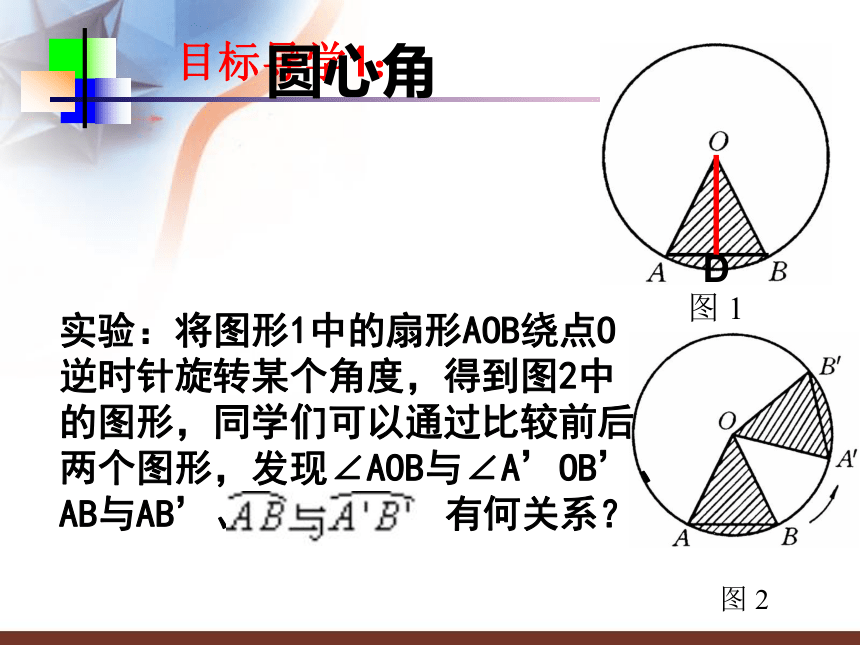
否与原图形重合?课前测评:圆的对称性及特性圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.圆也是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性实验:将图形1中的扇形AOB绕点O逆时针旋转某个角度,得到图2中的图形,同学们可以通过比较前后两个图形,发现∠AOB与∠A’OB’、AB与AB’、 有何关系?目标导学1:圆心角圆心角 顶点在圆心的角(如∠AOB).
弦心距 过圆心作弦的垂线,
圆心与垂足之间的
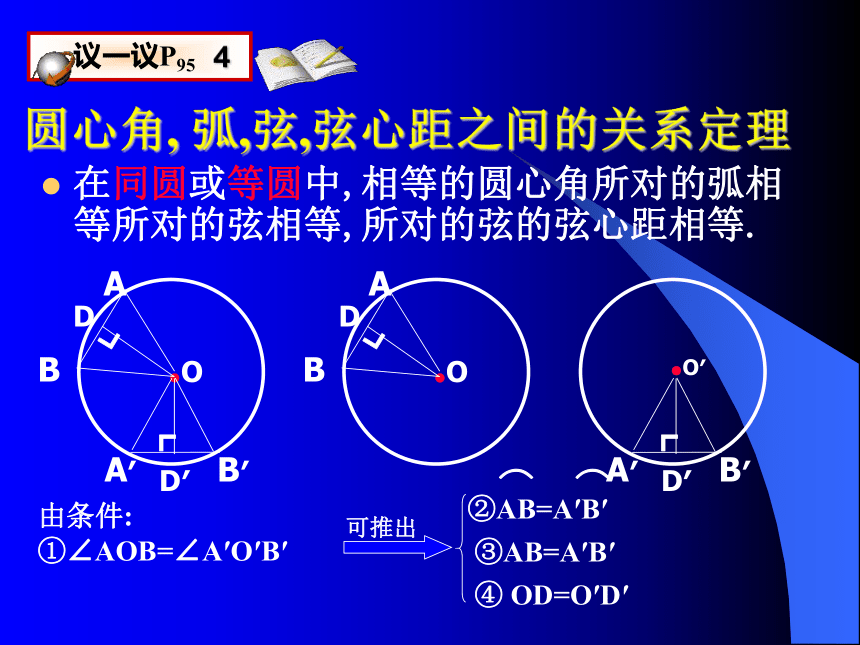
距离(如线段OD).ABEOplay观察:圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
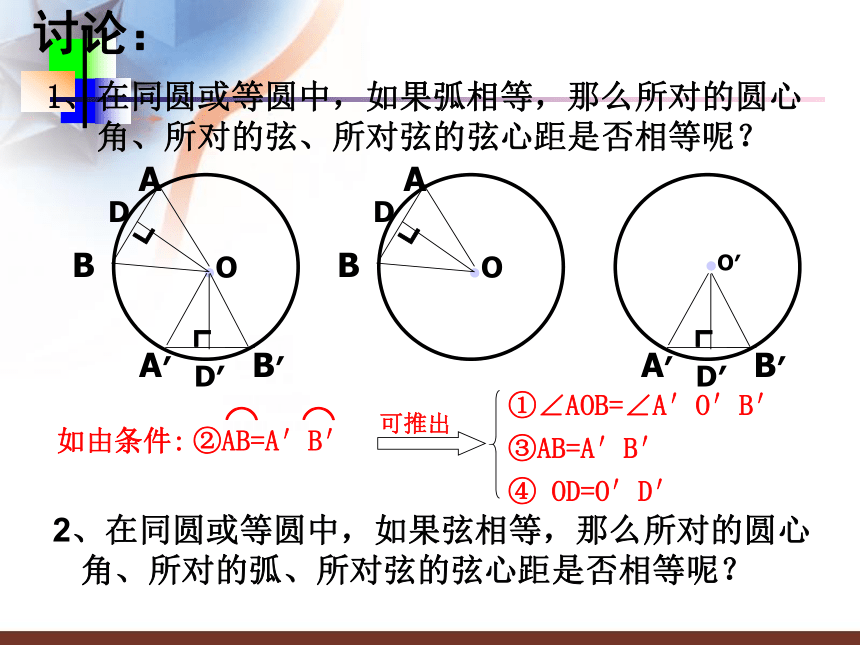
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′讨论:1、在同圆或等圆中,如果弧相等,那么所对的圆心
角、所对的弦、所对弦的弦心距是否相等呢?2、在同圆或等圆中,如果弦相等,那么所对的圆心
角、所对的弧、所对弦的弦心距是否相等呢?如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′例2:如图,在⊙O中,AB,CD是两条弦,
OE⊥AB,OF⊥CD ,
1)∠AOB=∠COD,那么OE与OF的大小
有什么关系?为什么?
2)如果OE=OF,那么AB与CD的大小有什
么关系? 的大小有什么关系?为
什么? ∠AOB与∠COD呢? ACFDEO 抢答题
已知:如图,AB,CD是⊙O的两条弦,
OE,OF为AB、CD的弦心距,根据这
节课所学的定理及推论填空:ABCFDEO(2)如果OE=OF,那么 , , ;(4)如果AB=CD,那么 , , 。(1)如果∠AOB=∠COD,那么 , , ;∠AOB=∠COD AB=CD OE=OF 1、如图,在⊙O中,弧AC=弧BD,
求∠2的度数。目标导学2:2、下面的说法正确吗?为什么?
如图,因为 根据圆心角、弧、弦、
弦心距的关系定理可知: 3、在⊙O中,a、b为弦,他们
的弦心距分别为 c、d,若a>b,则
A c<d B c>d
C c=d D 无法确定1、已知A、B是⊙O上的两点,∠AOB=120°,
C是弧AB的中点,试确定四边形OACB的形
状,并说明理由。达标练习:
1、如图,在⊙O中,弧AB=弧AC,
∠B=70°. 则∠C= .2、如图,AB是直径,弧BC=弧CD=弧DE,∠BOC=40°,则∠AOE= 。5、圆不仅是轴对称图形,它也
是 图形.它与其他中
心对称图形的区别是 。3、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB3、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB3、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB 本节课我们通过实验得到了圆不仅是中心对称图形,而且还是轴对称图形,而由圆的对称性又得出许多圆的性质,即
(1)在同一个圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。达标小结:(2)垂直于弦的直径平分这条弦,并且平
分弦所对的两条弧。作业P99习题
1、2、3
1、知道圆是中心对称图形和轴对称图形,并能运用其特有的性质推出在同一个圆中,圆心角、弧、弦之间的关系;
2、能运用圆心角、弧、弦之间的关系解决问题,培养善于从实验中获取知识的科学的方法。
3、在积极参与数学活动的过程中,体验发现问题、总结规律的态度以及养成质疑和独立思考的习惯。圆的对称性(3)1、圆是轴对称图形吗?
2、圆是中心对称图形吗?
3、圆绕着圆心旋转任意角度,是
否与原图形重合?课前测评:圆的对称性及特性圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.圆也是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性实验:将图形1中的扇形AOB绕点O逆时针旋转某个角度,得到图2中的图形,同学们可以通过比较前后两个图形,发现∠AOB与∠A’OB’、AB与AB’、 有何关系?目标导学1:圆心角圆心角 顶点在圆心的角(如∠AOB).
弦心距 过圆心作弦的垂线,
圆心与垂足之间的
距离(如线段OD).ABEOplay观察:圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′讨论:1、在同圆或等圆中,如果弧相等,那么所对的圆心
角、所对的弦、所对弦的弦心距是否相等呢?2、在同圆或等圆中,如果弦相等,那么所对的圆心
角、所对的弧、所对弦的弦心距是否相等呢?如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′例2:如图,在⊙O中,AB,CD是两条弦,
OE⊥AB,OF⊥CD ,
1)∠AOB=∠COD,那么OE与OF的大小
有什么关系?为什么?
2)如果OE=OF,那么AB与CD的大小有什
么关系? 的大小有什么关系?为
什么? ∠AOB与∠COD呢? ACFDEO 抢答题
已知:如图,AB,CD是⊙O的两条弦,
OE,OF为AB、CD的弦心距,根据这
节课所学的定理及推论填空:ABCFDEO(2)如果OE=OF,那么 , , ;(4)如果AB=CD,那么 , , 。(1)如果∠AOB=∠COD,那么 , , ;∠AOB=∠COD AB=CD OE=OF 1、如图,在⊙O中,弧AC=弧BD,
求∠2的度数。目标导学2:2、下面的说法正确吗?为什么?
如图,因为 根据圆心角、弧、弦、
弦心距的关系定理可知: 3、在⊙O中,a、b为弦,他们
的弦心距分别为 c、d,若a>b,则
A c<d B c>d
C c=d D 无法确定1、已知A、B是⊙O上的两点,∠AOB=120°,
C是弧AB的中点,试确定四边形OACB的形
状,并说明理由。达标练习:
1、如图,在⊙O中,弧AB=弧AC,
∠B=70°. 则∠C= .2、如图,AB是直径,弧BC=弧CD=弧DE,∠BOC=40°,则∠AOE= 。5、圆不仅是轴对称图形,它也
是 图形.它与其他中
心对称图形的区别是 。3、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB3、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB3、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB 本节课我们通过实验得到了圆不仅是中心对称图形,而且还是轴对称图形,而由圆的对称性又得出许多圆的性质,即
(1)在同一个圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。达标小结:(2)垂直于弦的直径平分这条弦,并且平
分弦所对的两条弧。作业P99习题
1、2、3
