§3-3 圆周角和圆心角的关系(1)圆周角定理[下学期]
文档属性
| 名称 | §3-3 圆周角和圆心角的关系(1)圆周角定理[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 339.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-05 15:34:00 | ||
图片预览


文档简介
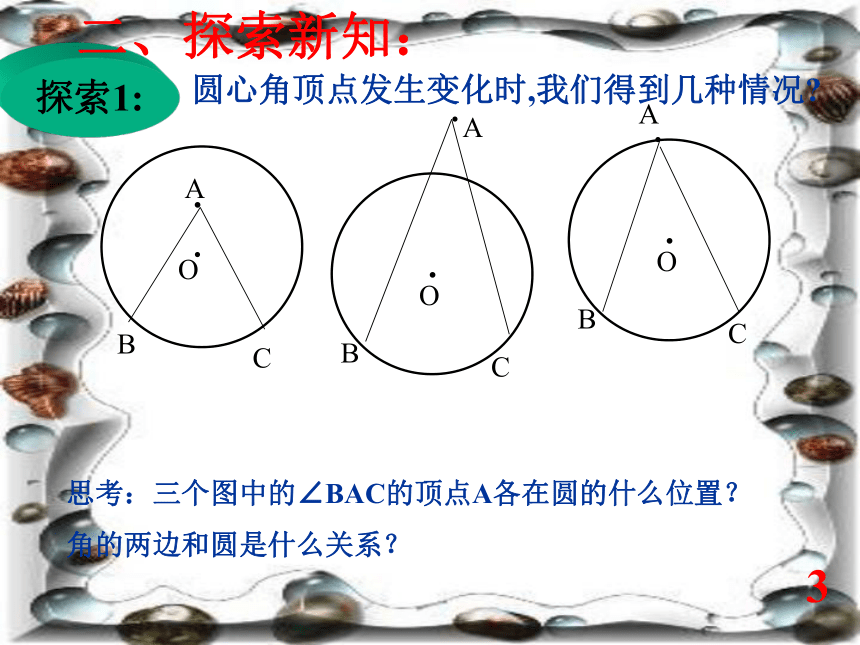
课件20张PPT。九年级数学(下)第三章 圆3. 圆周角和圆心角的关系(1)圆周角定理good!一、旧知回放:1.圆心角的定义?答:相等.答:顶点在圆心的角叫圆心角.2.圆心角的度数和它所对的弧的 度数的关系? 2圆心角顶点发生变化时,我们得到几种情况?A.OBCAA探索1:二、探索新知: 3...思考:三个图中的∠BAC的顶点A各在圆的什么位置?
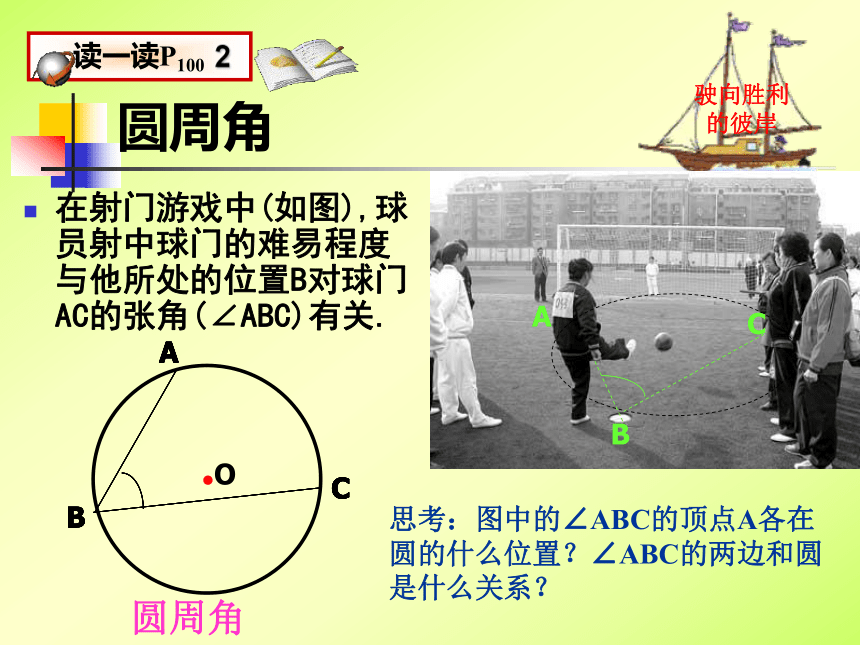
角的两边和圆是什么关系?圆周角在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.驶向胜利的彼岸思考:图中的∠ABC的顶点A各在圆的什么位置?∠ABC的两边和圆是什么关系?圆周角探索2:你能仿照圆心角的定义给圆周角下个定义吗?特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
叫圆周角.
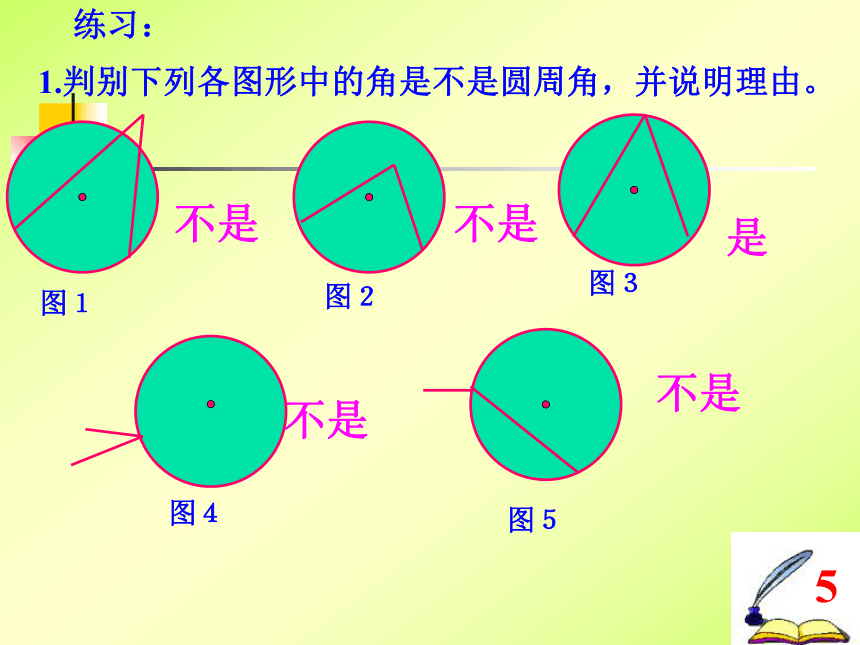
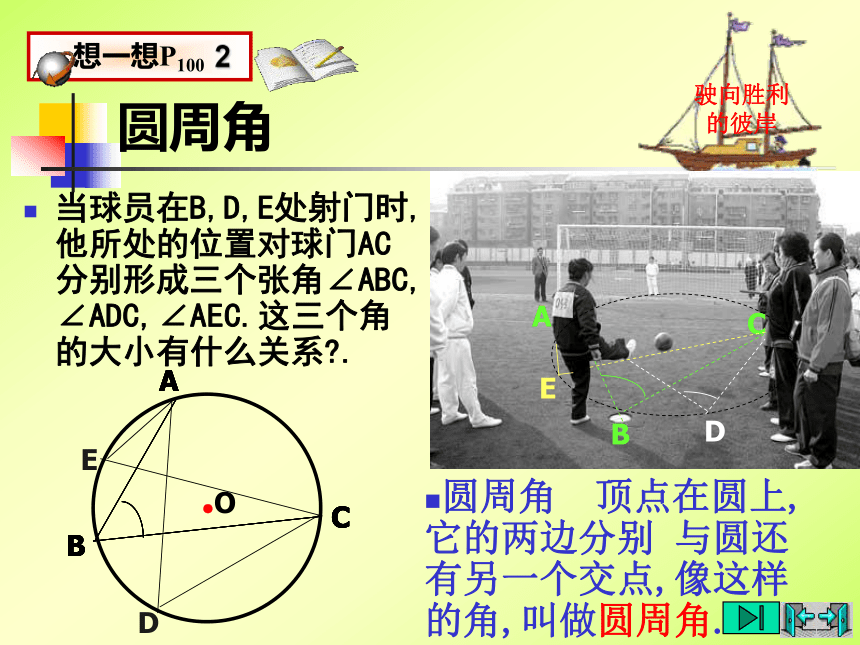
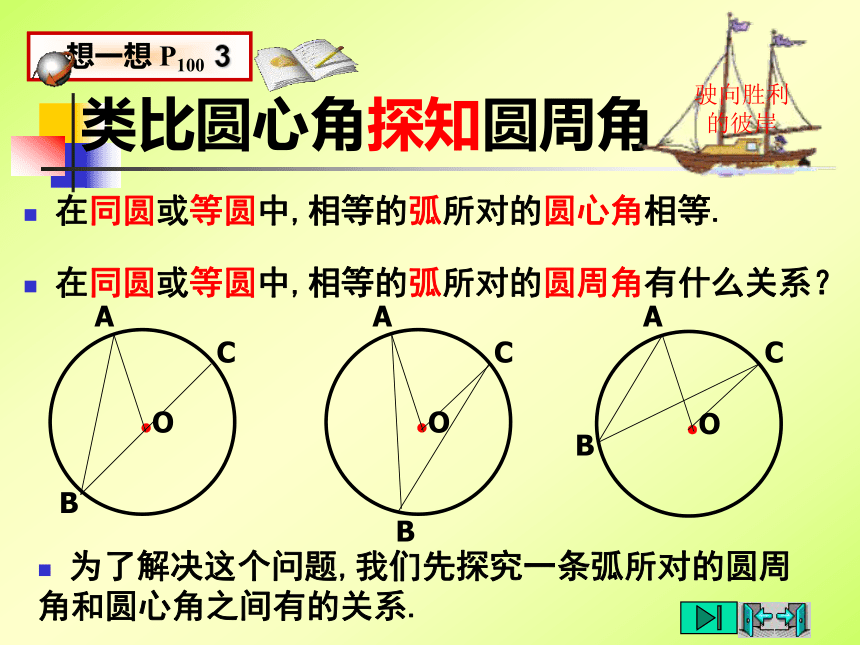
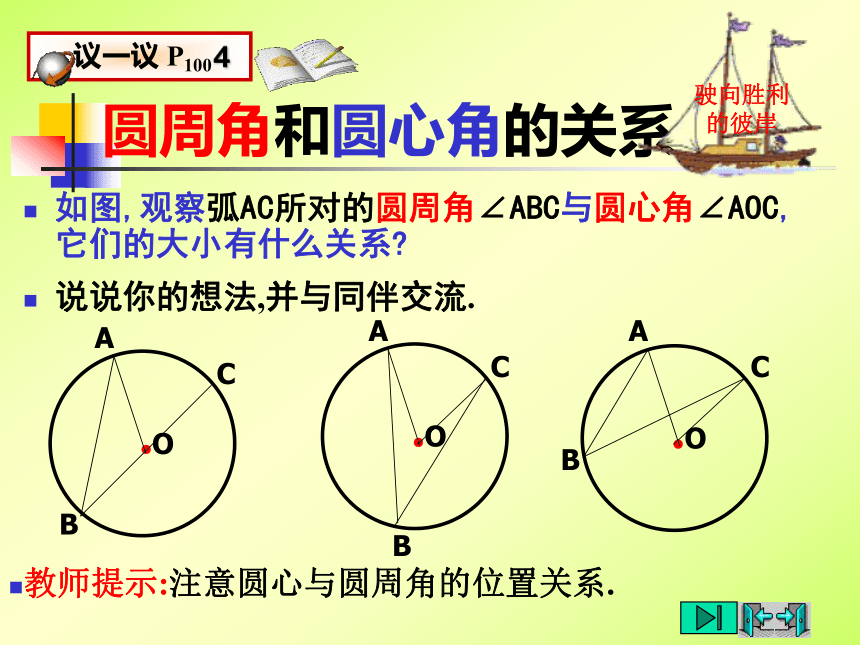
4练习:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是5图1图2图3图4图5圆周角当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.驶向胜利的彼岸圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系?驶向胜利的彼岸 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.圆周角和圆心角的关系如图,观察弧AC所对的圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.驶向胜利的彼岸教师提示:注意圆心与圆周角的位置关系.驶向胜利的彼岸圆周角和圆心角的关系1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.驶向胜利的彼岸圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,驶向胜利的彼岸圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴ ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.驶向胜利的彼岸老师提示:圆周角定理是承上启下的知识点,要予以重视.即 ∠ABC = ∠AOC.练习:2.如图,圆心角∠AOB=100°,则∠ACB=___。1.求圆中角X的度数130° C C D B做做看,收获知多少?一、判断
1、顶点在圆上的角叫圆周角。( )
2、圆周角的度数等于所对弧的度数的一半。( )
二、计算
半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的
圆周角的度数是 。×√.O60°或120°驶向胜利的彼岸思考与巩固1.如图,在⊙O中,∠BOC=50°,求∠A的大小. 2.举出生活中含有圆周角的例子.解: ∠A = ∠BOC = 25°.习题1.如图:OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.证明:∠ACB= ∠AOB12∠BAC= ∠BOC2∠AOB=2∠BOC∠ACB=2∠BAC四、新知应用:1 规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理分析:AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB.
BC所对圆周角是∠ BAC , 圆心角是∠BOC, 则∠ BAC= ∠BOC ⌒
⌒
一 、这节课主要学习了两个知识点:
1、圆周角定义。
2、圆周角定理及其定理应用。
二、方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法。五、总结扩展:三、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用驶向胜利的彼岸拓展 化心动为行动1.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
3.如图(3),AB是直径,你能确定∠C的度数吗?
角的两边和圆是什么关系?圆周角在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.驶向胜利的彼岸思考:图中的∠ABC的顶点A各在圆的什么位置?∠ABC的两边和圆是什么关系?圆周角探索2:你能仿照圆心角的定义给圆周角下个定义吗?特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
叫圆周角.
4练习:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是5图1图2图3图4图5圆周角当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.驶向胜利的彼岸圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系?驶向胜利的彼岸 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.圆周角和圆心角的关系如图,观察弧AC所对的圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.驶向胜利的彼岸教师提示:注意圆心与圆周角的位置关系.驶向胜利的彼岸圆周角和圆心角的关系1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.驶向胜利的彼岸圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,驶向胜利的彼岸圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴ ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.驶向胜利的彼岸老师提示:圆周角定理是承上启下的知识点,要予以重视.即 ∠ABC = ∠AOC.练习:2.如图,圆心角∠AOB=100°,则∠ACB=___。1.求圆中角X的度数130° C C D B做做看,收获知多少?一、判断
1、顶点在圆上的角叫圆周角。( )
2、圆周角的度数等于所对弧的度数的一半。( )
二、计算
半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的
圆周角的度数是 。×√.O60°或120°驶向胜利的彼岸思考与巩固1.如图,在⊙O中,∠BOC=50°,求∠A的大小. 2.举出生活中含有圆周角的例子.解: ∠A = ∠BOC = 25°.习题1.如图:OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.证明:∠ACB= ∠AOB12∠BAC= ∠BOC2∠AOB=2∠BOC∠ACB=2∠BAC四、新知应用:1 规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理分析:AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB.
BC所对圆周角是∠ BAC , 圆心角是∠BOC, 则∠ BAC= ∠BOC ⌒
⌒
一 、这节课主要学习了两个知识点:
1、圆周角定义。
2、圆周角定理及其定理应用。
二、方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法。五、总结扩展:三、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用驶向胜利的彼岸拓展 化心动为行动1.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
3.如图(3),AB是直径,你能确定∠C的度数吗?
