圆周角和圆心角的关系(2)[下学期]
文档属性
| 名称 | 圆周角和圆心角的关系(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 106.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-01-12 00:00:00 | ||
图片预览


文档简介
(共10张PPT)
九年级数学(下)第三章
圆
3. 圆周角和圆心角的关系(2)
圆周角定理的推论
问题解答
1、圆周角定理的推论1:
同圆或等圆中,同弧或等弧所对的圆周角相等;
2、圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
用于找相等的角
用于判断某个圆周角是否是直角
用于判断某条线是否过圆心
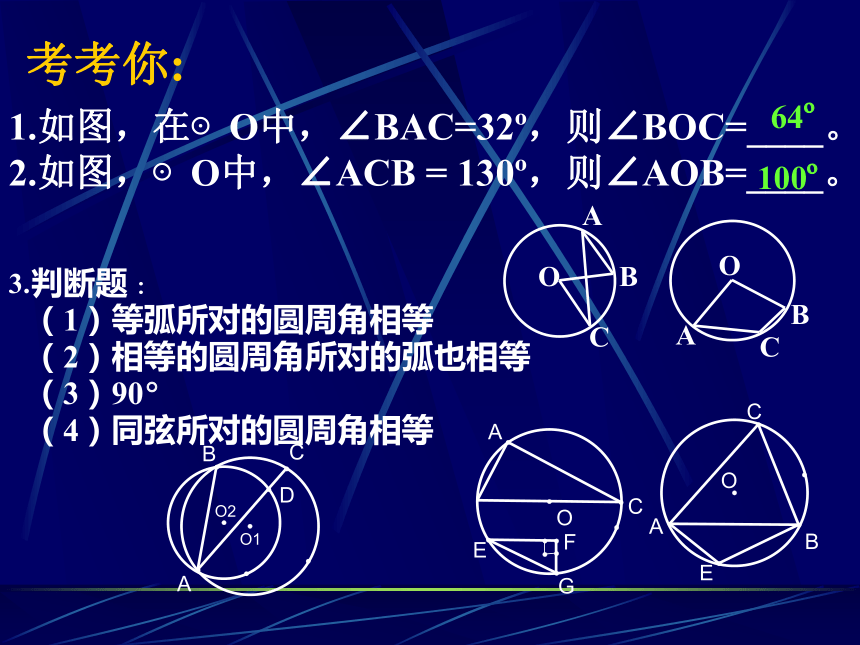
1.如图,在⊙O中,∠BAC=32 ,则∠BOC=____。
2.如图,⊙O中,∠ACB = 130 ,则∠AOB=____。
考考你:
64
100
A
O
C
B
A
O
C
B
3.
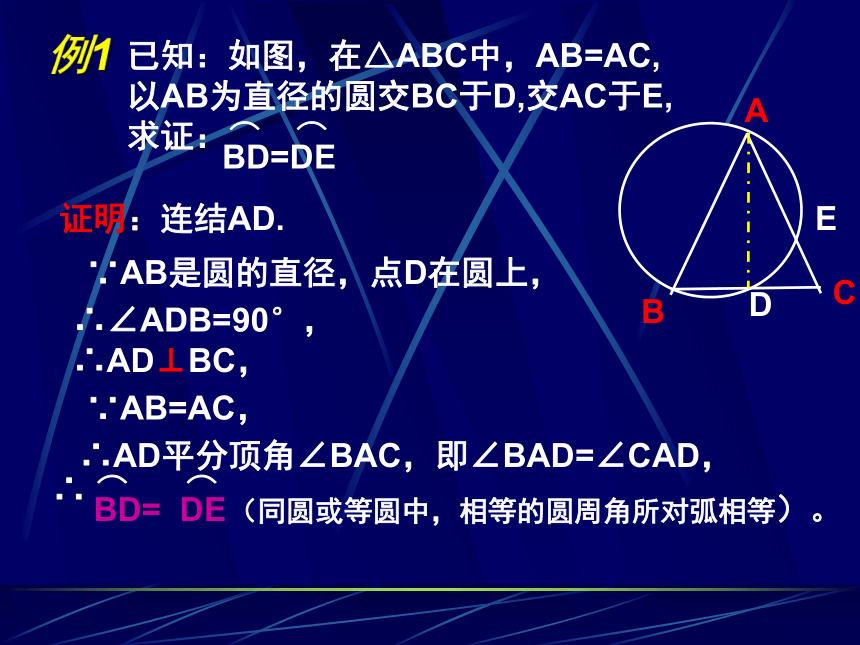
例1
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
证明:连结AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分顶角∠BAC,即∠BAD=∠CAD,
∴ ⌒ ⌒
BD= DE
(同圆或等圆中,相等的圆周角所对弧相等)。
A
B
C
D
E
练习:
如图,P是△ABC的外接圆上的一点
∠APC=∠CPB=60°。求证:△ABC是等边三角形
·
·
A
P
B
C
O
证明:∵∠ABC和∠APC
都是 ⌒ 所对的圆周角。
AC
∴∠ABC=∠APC=60°
(同弧所对的圆周角相等)
同理,∵∠BAC和∠CPB都是 ⌒ 所对的圆周角,
BC
∴∠BAC=∠CPB=60°。
∴△ABC等边三角形。
例2.
A
1. 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则OC与AD的
位置关系是________。
2.在上题中,若AC = 2cm,则AD = __cm。
A
B
C
D
O
O1
OC与BD的位置关系是________。
小结与作业
1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
3、证明题思路的寻找方法如何?
讨论与思考
A
B
C
D
O
E
如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?
结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE
九年级数学(下)第三章
圆
3. 圆周角和圆心角的关系(2)
圆周角定理的推论
问题解答
1、圆周角定理的推论1:
同圆或等圆中,同弧或等弧所对的圆周角相等;
2、圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
用于找相等的角
用于判断某个圆周角是否是直角
用于判断某条线是否过圆心
1.如图,在⊙O中,∠BAC=32 ,则∠BOC=____。
2.如图,⊙O中,∠ACB = 130 ,则∠AOB=____。
考考你:
64
100
A
O
C
B
A
O
C
B
3.
例1
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
证明:连结AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分顶角∠BAC,即∠BAD=∠CAD,
∴ ⌒ ⌒
BD= DE
(同圆或等圆中,相等的圆周角所对弧相等)。
A
B
C
D
E
练习:
如图,P是△ABC的外接圆上的一点
∠APC=∠CPB=60°。求证:△ABC是等边三角形
·
·
A
P
B
C
O
证明:∵∠ABC和∠APC
都是 ⌒ 所对的圆周角。
AC
∴∠ABC=∠APC=60°
(同弧所对的圆周角相等)
同理,∵∠BAC和∠CPB都是 ⌒ 所对的圆周角,
BC
∴∠BAC=∠CPB=60°。
∴△ABC等边三角形。
例2.
A
1. 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则OC与AD的
位置关系是________。
2.在上题中,若AC = 2cm,则AD = __cm。
A
B
C
D
O
O1
OC与BD的位置关系是________。
小结与作业
1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
3、证明题思路的寻找方法如何?
讨论与思考
A
B
C
D
O
E
如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?
结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE
