圆周角和圆心角的关系[下学期]
图片预览



文档简介
课件21张PPT。圆周角和圆心角的关系韩城市涧南中学
薛改菊 张双年
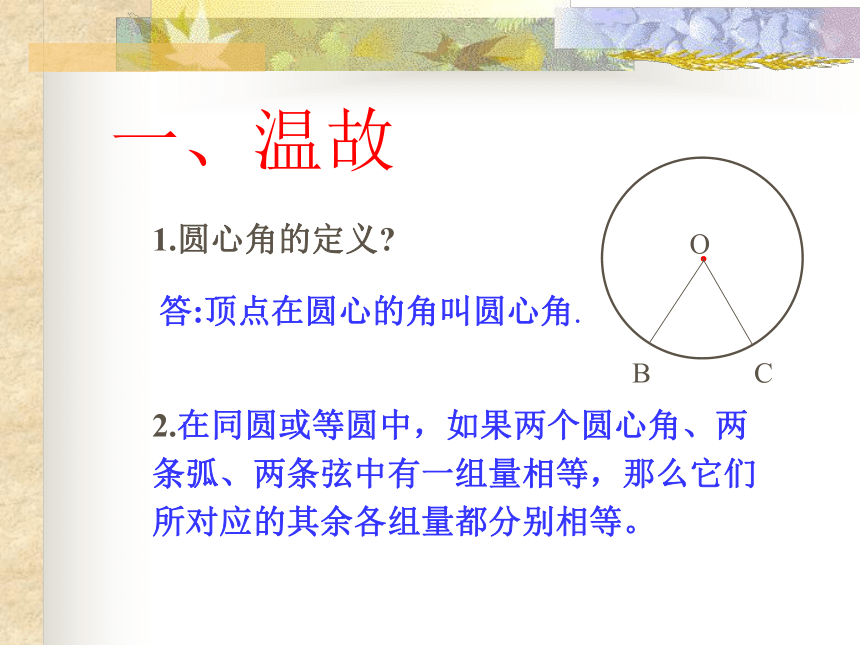
1.圆心角的定义?答:顶点在圆心的角叫圆心角.
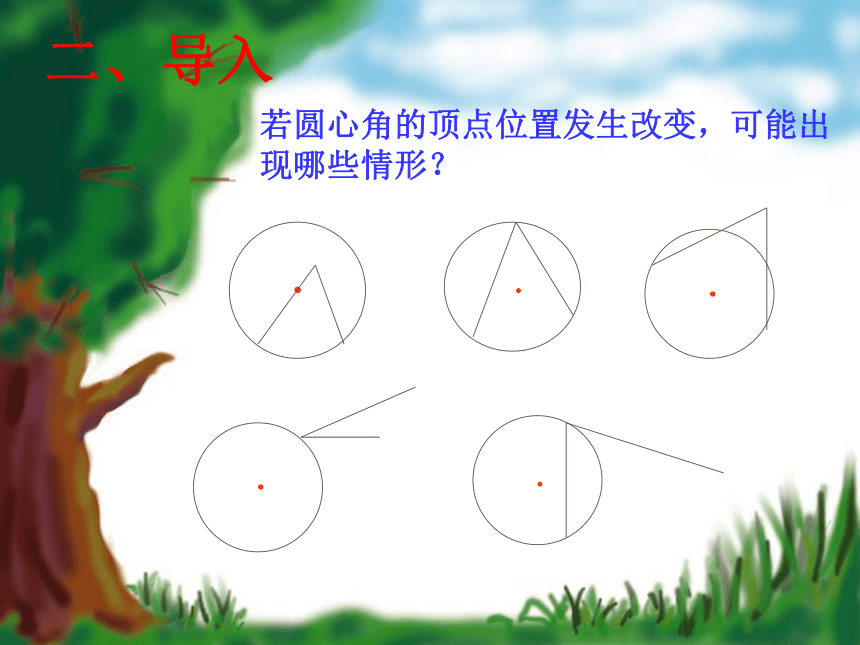
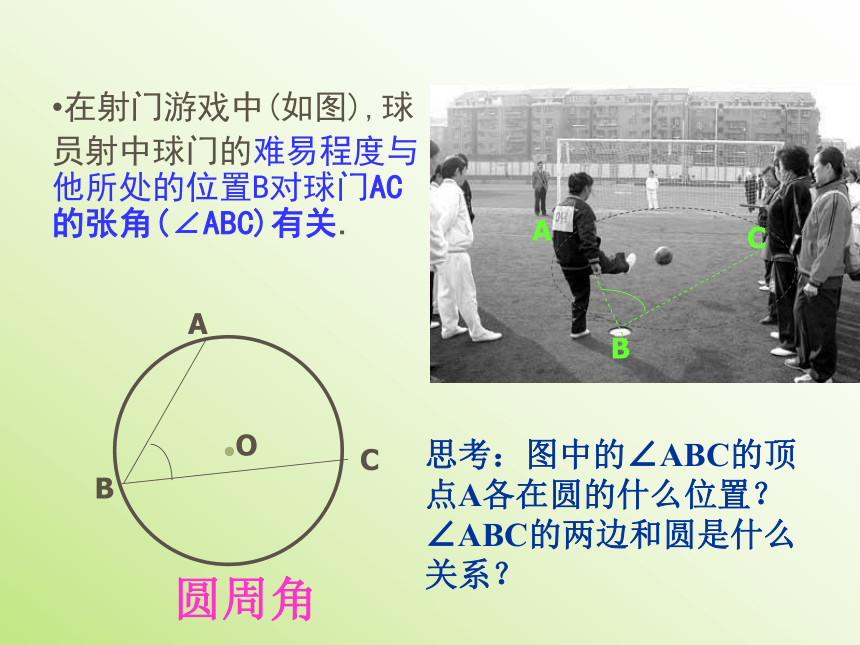
一、温故2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。二、导入若圆心角的顶点位置发生改变,可能出现哪些情形?在射门游戏中(如图),球
员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.圆周角思考:图中的∠ABC的顶点A各在圆的什么位置?∠ABC的两边和圆是什么关系?1.你能用一句话来总结
“什么是圆周角”吗?答:顶点在圆上,角的两边
分别和圆相交的角,叫圆
周角。注意:⑴顶点在圆上
⑵角的两边分别和圆相交三.新知
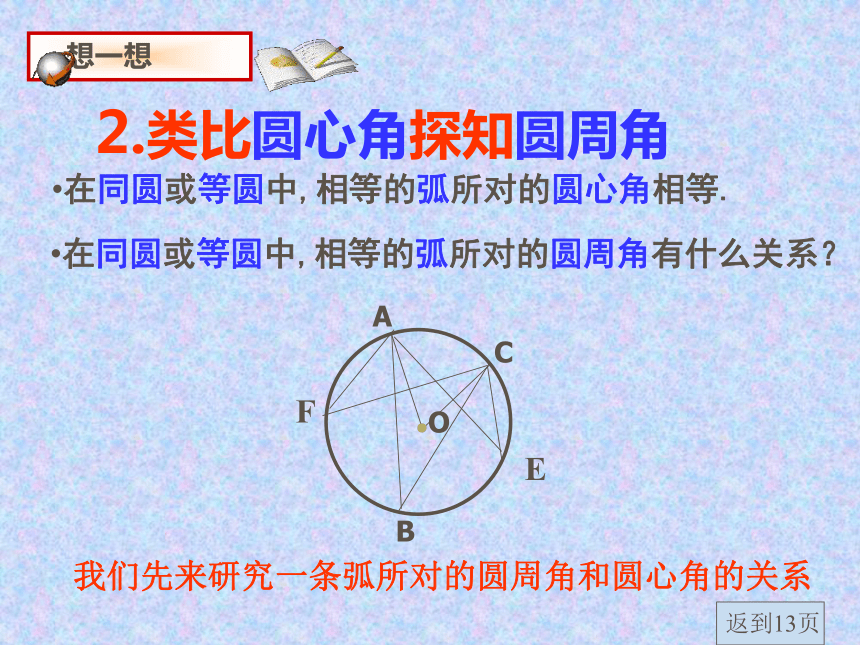
我们知道,角的要素有两个,一个是顶点,一个是两边,而这儿的圆心角只提到顶点在圆心,没有提两边与圆的情况,但圆周角提到了两个要素,为什么呢?想一想2.类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
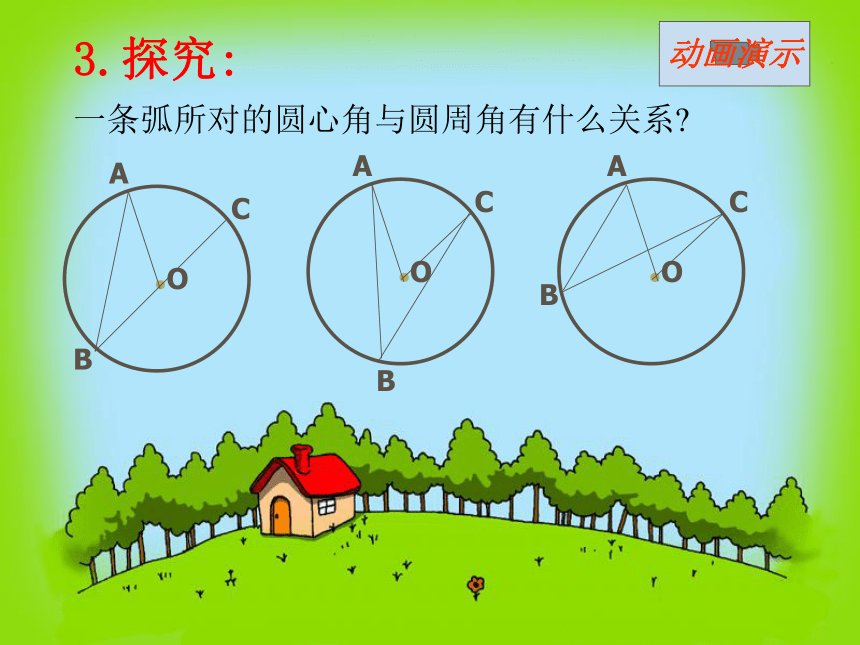
我们先来研究一条弧所对的圆周角和圆心角的关系返到13页3.探究:
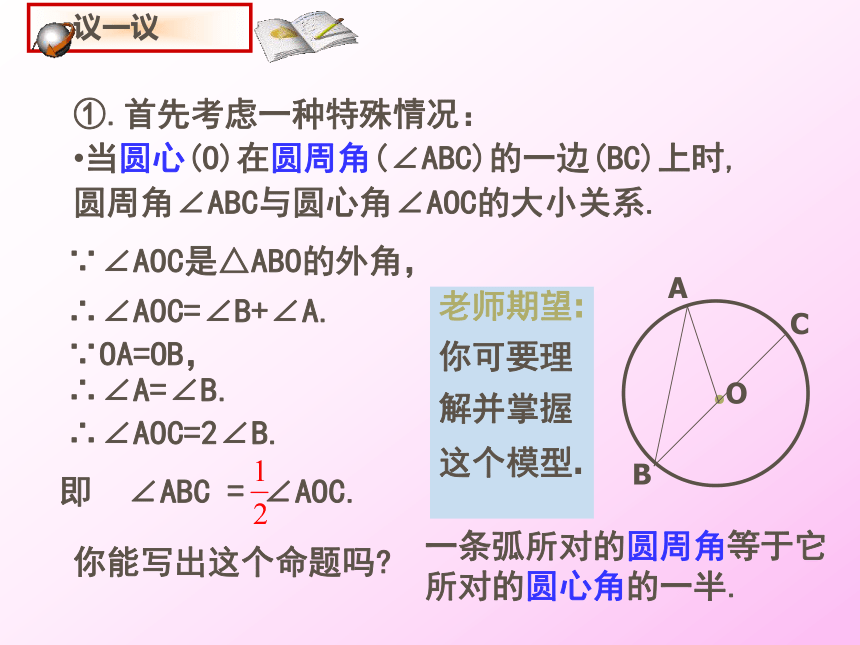
一条弧所对的圆心角与圆周角有什么关系?动画演示①.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,
圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
你能写出这个命题吗?
老师期望:
你可要理
解并掌握
这个模型.
一条弧所对的圆周角等于它
所对的圆心角的一半.
③当圆心(O)在圆周角(∠ABC)的外部时,圆周
角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否也转化为①的情况?
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?
一条弧所对的圆周角等于
它所对的圆心角的一半.
②当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否转化为①的情况?
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于它
所对的圆心角的一半.
圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是圆周角定理:一条弧所对的圆周角等于它所对的
圆心角的一半.
想一想:你能对以上的证明做出一个归纳吗?①辅助线②数学思想方法 请同学们再用这个定理去验证一下前面的你所做过的那个猜想,如何呢? 用一句话来概括一下?推论:在同圆或等圆中,同弧或等弧所对 的圆周角相等4.练习····100°AO20°O90°ABABBCOBACC(1)(2)(3)(4)AB为直径,求∠ACB求∠AOB求∠AOB求∠A由上面的(3)和(4),大家发现了什么?试着用一句话来说说.推论:直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.5.例题.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB.BD与CD的大小有什么关系?解:BD=CD.理由是:连接AD.∵AB是⊙O的直径,∴∠ADB=90°即AD⊥BC又∵AC=AB∴BD=CD四.知识运用 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图所示,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁. ·o(1)当船与两个灯塔的夹角∠α大于
“危险角”时,船位于哪个区域?为什
么?(2)当船与两个灯塔的夹角∠α小
于“危险角”时,船位于哪个区域?
为什么?答(1)船位于暗礁区域内(即圆o内).
理由:假设船在⊙O上,则有∠α=∠C,这与
∠α> ∠ C矛盾.所以船不可能在⊙O上;
假设船在⊙O外,则有∠ α< ∠AEB,即
∠ α < ∠C,这与∠ α > ∠C矛盾.所以
船不可能在⊙O外.
因此,船只能位于⊙O内.(2)船位于暗礁区域外(即⊙O外).五、谈谈你的收获:(1)圆周角定义(2)圆周角定理(3)圆周角定理的推论(5)数学思想方法(4)辅助线六.作业1.随堂练习第3题
2.习题3.5第2题敬请各位老师批评指导!
薛改菊 张双年
1.圆心角的定义?答:顶点在圆心的角叫圆心角.
一、温故2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。二、导入若圆心角的顶点位置发生改变,可能出现哪些情形?在射门游戏中(如图),球
员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.圆周角思考:图中的∠ABC的顶点A各在圆的什么位置?∠ABC的两边和圆是什么关系?1.你能用一句话来总结
“什么是圆周角”吗?答:顶点在圆上,角的两边
分别和圆相交的角,叫圆
周角。注意:⑴顶点在圆上
⑵角的两边分别和圆相交三.新知
我们知道,角的要素有两个,一个是顶点,一个是两边,而这儿的圆心角只提到顶点在圆心,没有提两边与圆的情况,但圆周角提到了两个要素,为什么呢?想一想2.类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
我们先来研究一条弧所对的圆周角和圆心角的关系返到13页3.探究:
一条弧所对的圆心角与圆周角有什么关系?动画演示①.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,
圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
你能写出这个命题吗?
老师期望:
你可要理
解并掌握
这个模型.
一条弧所对的圆周角等于它
所对的圆心角的一半.
③当圆心(O)在圆周角(∠ABC)的外部时,圆周
角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否也转化为①的情况?
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?
一条弧所对的圆周角等于
它所对的圆心角的一半.
②当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否转化为①的情况?
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于它
所对的圆心角的一半.
圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是圆周角定理:一条弧所对的圆周角等于它所对的
圆心角的一半.
想一想:你能对以上的证明做出一个归纳吗?①辅助线②数学思想方法 请同学们再用这个定理去验证一下前面的你所做过的那个猜想,如何呢? 用一句话来概括一下?推论:在同圆或等圆中,同弧或等弧所对 的圆周角相等4.练习····100°AO20°O90°ABABBCOBACC(1)(2)(3)(4)AB为直径,求∠ACB求∠AOB求∠AOB求∠A由上面的(3)和(4),大家发现了什么?试着用一句话来说说.推论:直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.5.例题.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB.BD与CD的大小有什么关系?解:BD=CD.理由是:连接AD.∵AB是⊙O的直径,∴∠ADB=90°即AD⊥BC又∵AC=AB∴BD=CD四.知识运用 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图所示,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁. ·o(1)当船与两个灯塔的夹角∠α大于
“危险角”时,船位于哪个区域?为什
么?(2)当船与两个灯塔的夹角∠α小
于“危险角”时,船位于哪个区域?
为什么?答(1)船位于暗礁区域内(即圆o内).
理由:假设船在⊙O上,则有∠α=∠C,这与
∠α> ∠ C矛盾.所以船不可能在⊙O上;
假设船在⊙O外,则有∠ α< ∠AEB,即
∠ α < ∠C,这与∠ α > ∠C矛盾.所以
船不可能在⊙O外.
因此,船只能位于⊙O内.(2)船位于暗礁区域外(即⊙O外).五、谈谈你的收获:(1)圆周角定义(2)圆周角定理(3)圆周角定理的推论(5)数学思想方法(4)辅助线六.作业1.随堂练习第3题
2.习题3.5第2题敬请各位老师批评指导!
