2022-2023学年人教版八年级数学上册12.3.1角平分线的性质 课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.3.1角平分线的性质 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 19:16:43 | ||
图片预览


文档简介
(共22张PPT)
人教版 八年级上
12.3 角的平分线的性质
第十二章 全等三角形
第1课时 角平分线的性质
学习目标
1、掌握用尺规作已知角的平分线的方法;
2、理解角的平分线的性质并能初步运用。
新知导入
在一个三角形居住区内修有一个学校P,P到AB、BC、CA三边的距离都相等,请在三角形居住区内标出学校P的位置,P在何处?
A
B
C
新知讲解
知识点1、角的平分线的性质
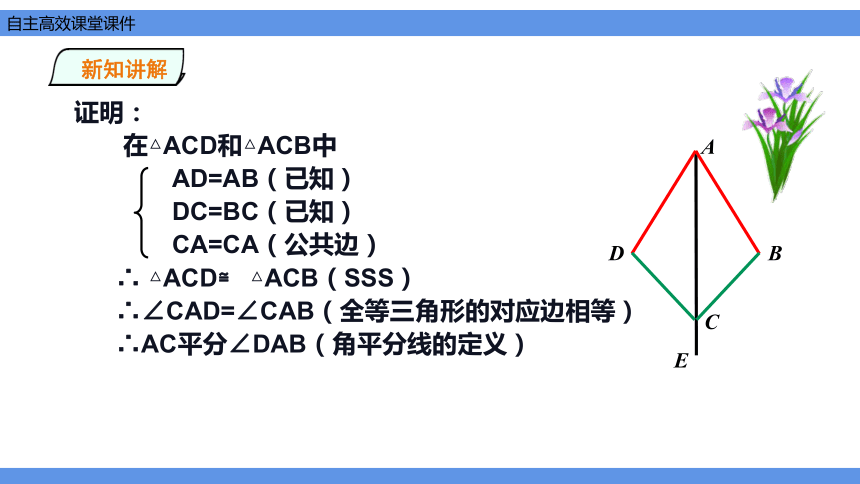
活动1、如图,是一个角平分仪,其中AB=AD,BC=DC。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,
你能说明它的道理吗
A
D
B
C
E
新知讲解
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的对应边相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
新知讲解
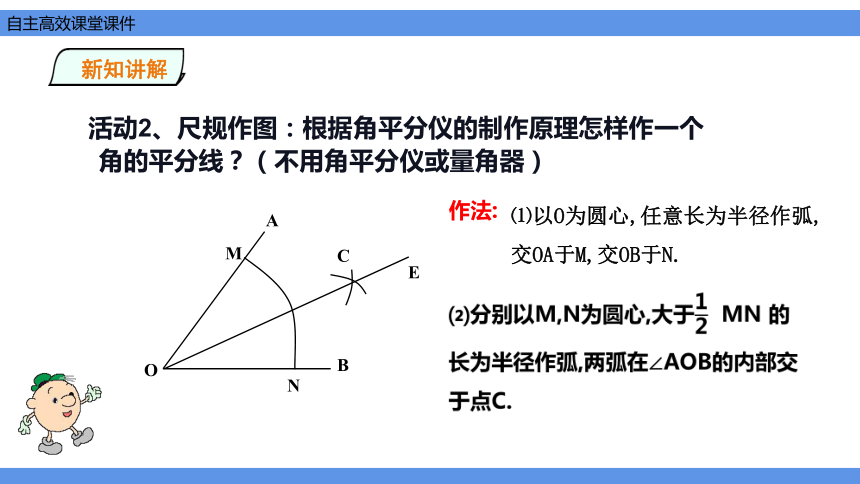
活动2、尺规作图:根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
M
N
作法:
⑴以O为圆心,任意长为半径作弧,交OA于M,交OB于N.
新知讲解
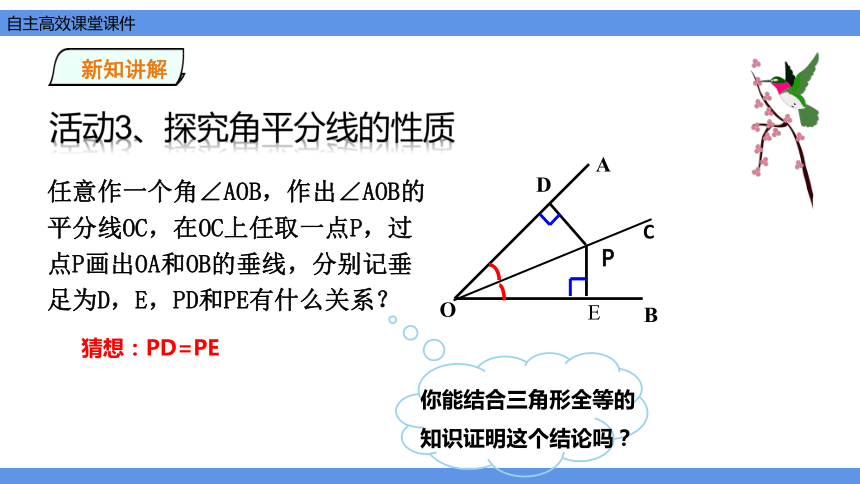
任意作一个角∠AOB,作出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA和OB的垂线,分别记垂足为D,E,PD和PE有什么关系?
D
P
E
A
O
B
C
猜想:PD=PE
你能结合三角形全等的知识证明这个结论吗?
活动3、探究角平分线的性质
新知讲解
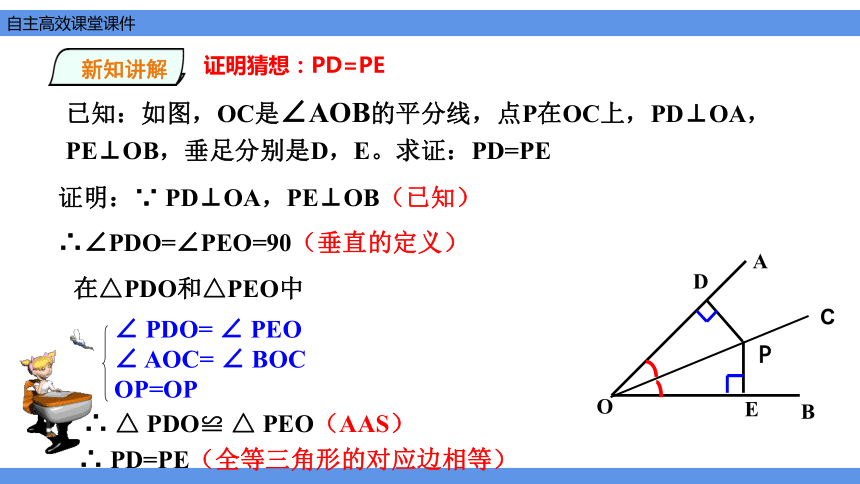
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。求证:PD=PE
证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴ PD=PE(全等三角形的对应边相等)
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO(AAS)
D
P
E
A
O
B
C
证明猜想:PD=PE
新知讲解
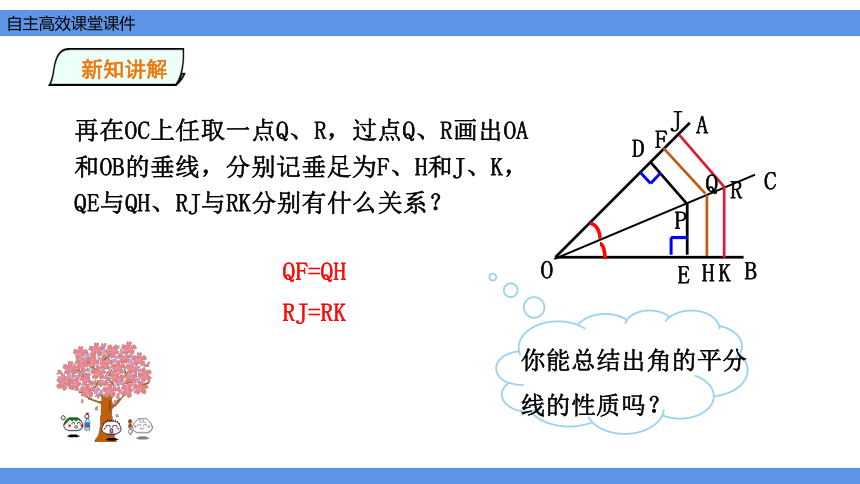
再在OC上任取一点Q、R,过点Q、R画出OA和OB的垂线,分别记垂足为F、H和J、K,QE与QH、RJ与RK分别有什么关系?
D
P
E
A
O
B
C
QF=QH
你能总结出角的平分线的性质吗?
RJ=RK
Q
R
J
F
H
K
新知讲解
归纳:角平分线的性质
定理:角的平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵ ∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴PD=PE
(角的平分线上的点到角的两边的距离相等)
推理的理由有三个,必须写完全,不能少了任何一个。
新知讲解
角平分线的性质
角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
新知讲解
证明几何命题的一般步骤:
1、明确命题的已知和求证
2、根据题意,画出图形,并用数学符号表示已知和求证;
3、经过分析,找出由已知推出求证的途径,写出证明过程。
归纳:
巩固练习
1.如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A.PC=PD B.OC=OD
C.∠CPO=∠DPO D.OC=PC
D
巩固练习
2.如图,已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,垂足分别为M,N.求证:PM=PN.
证明:∵OD平分∠AOB,∠1=∠2,
又∵OA=OB,OD=OD,∴△AOD≌△BOD,
∴∠3=∠4,
又∵PM⊥DB,PN⊥DA,
∴PM=PN(角平分线上的点到角两边的距离相等).
课堂总结
小结:这节课我们学到了什么?在生活中有那些用到了我们今天学到的知识。
1、性质:角平分线上的点到这个角的两边距离相等.
2、判定:到角两边距离相等的点在这个角的平分线上
角平分线可以看作是到角两边距离相等的点的集合。
巩固诊断
1.如图,AD是△ABC的角平分线,若AB=10,AC=8,则S△ABD∶S△ADC=( )
A.1∶1
B.4∶5
C.5∶4
D.16∶25
C
D
C
A
B
巩固诊断
2.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6 C.4 D.2
巩固诊断
3.如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF相交于点D,则:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
A.只有①
B.只有②
C.只有①和②
D.①②③
D
巩固诊断
4.l1,l2,l3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站的位置共有( )
A.1处 B.2处 C.3处 D.4处
D
巩固诊断
5.如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,M为OP上任意一点,连接CM,DM,则CM和DM的大小关系是 .
相等
巩固诊断
6.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,BD=DF,求证:CF=EB.
D
B
F
A
C
E
巩固诊断
7.如图,在四边形ABCD中,∠B=∠C,点E在边BC上,AE平分∠BAD,DE平分∠ADC.
求证:BE=CE.
过点E作EG⊥AB于G,EH⊥AD于H,EM⊥BC于M
G
H
M
∵AE平分∠BAD,EG⊥AB, EH⊥AD
∴EG=EH,∠BGE=900
∴EM=EH,∠EMC=900
∴EG=EM,∠BGE=∠EMC=900
在△BGE和△CME中
A
B
C
D
E
∠B=∠C
∠BGE=∠EMC
EG=EM
∴△BGE≌△CME(AAS)
∴BE=CE
又∵DE平分∠ADC,EH⊥AD, EM⊥BC
人教版 八年级上
12.3 角的平分线的性质
第十二章 全等三角形
第1课时 角平分线的性质
学习目标
1、掌握用尺规作已知角的平分线的方法;
2、理解角的平分线的性质并能初步运用。
新知导入
在一个三角形居住区内修有一个学校P,P到AB、BC、CA三边的距离都相等,请在三角形居住区内标出学校P的位置,P在何处?
A
B
C
新知讲解
知识点1、角的平分线的性质
活动1、如图,是一个角平分仪,其中AB=AD,BC=DC。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,
你能说明它的道理吗
A
D
B
C
E
新知讲解
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的对应边相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
新知讲解
活动2、尺规作图:根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
M
N
作法:
⑴以O为圆心,任意长为半径作弧,交OA于M,交OB于N.
新知讲解
任意作一个角∠AOB,作出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA和OB的垂线,分别记垂足为D,E,PD和PE有什么关系?
D
P
E
A
O
B
C
猜想:PD=PE
你能结合三角形全等的知识证明这个结论吗?
活动3、探究角平分线的性质
新知讲解
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。求证:PD=PE
证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴ PD=PE(全等三角形的对应边相等)
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO(AAS)
D
P
E
A
O
B
C
证明猜想:PD=PE
新知讲解
再在OC上任取一点Q、R,过点Q、R画出OA和OB的垂线,分别记垂足为F、H和J、K,QE与QH、RJ与RK分别有什么关系?
D
P
E
A
O
B
C
QF=QH
你能总结出角的平分线的性质吗?
RJ=RK
Q
R
J
F
H
K
新知讲解
归纳:角平分线的性质
定理:角的平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵ ∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴PD=PE
(角的平分线上的点到角的两边的距离相等)
推理的理由有三个,必须写完全,不能少了任何一个。
新知讲解
角平分线的性质
角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
新知讲解
证明几何命题的一般步骤:
1、明确命题的已知和求证
2、根据题意,画出图形,并用数学符号表示已知和求证;
3、经过分析,找出由已知推出求证的途径,写出证明过程。
归纳:
巩固练习
1.如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A.PC=PD B.OC=OD
C.∠CPO=∠DPO D.OC=PC
D
巩固练习
2.如图,已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,垂足分别为M,N.求证:PM=PN.
证明:∵OD平分∠AOB,∠1=∠2,
又∵OA=OB,OD=OD,∴△AOD≌△BOD,
∴∠3=∠4,
又∵PM⊥DB,PN⊥DA,
∴PM=PN(角平分线上的点到角两边的距离相等).
课堂总结
小结:这节课我们学到了什么?在生活中有那些用到了我们今天学到的知识。
1、性质:角平分线上的点到这个角的两边距离相等.
2、判定:到角两边距离相等的点在这个角的平分线上
角平分线可以看作是到角两边距离相等的点的集合。
巩固诊断
1.如图,AD是△ABC的角平分线,若AB=10,AC=8,则S△ABD∶S△ADC=( )
A.1∶1
B.4∶5
C.5∶4
D.16∶25
C
D
C
A
B
巩固诊断
2.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6 C.4 D.2
巩固诊断
3.如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF相交于点D,则:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
A.只有①
B.只有②
C.只有①和②
D.①②③
D
巩固诊断
4.l1,l2,l3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站的位置共有( )
A.1处 B.2处 C.3处 D.4处
D
巩固诊断
5.如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,M为OP上任意一点,连接CM,DM,则CM和DM的大小关系是 .
相等
巩固诊断
6.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,BD=DF,求证:CF=EB.
D
B
F
A
C
E
巩固诊断
7.如图,在四边形ABCD中,∠B=∠C,点E在边BC上,AE平分∠BAD,DE平分∠ADC.
求证:BE=CE.
过点E作EG⊥AB于G,EH⊥AD于H,EM⊥BC于M
G
H
M
∵AE平分∠BAD,EG⊥AB, EH⊥AD
∴EG=EH,∠BGE=900
∴EM=EH,∠EMC=900
∴EG=EM,∠BGE=∠EMC=900
在△BGE和△CME中
A
B
C
D
E
∠B=∠C
∠BGE=∠EMC
EG=EM
∴△BGE≌△CME(AAS)
∴BE=CE
又∵DE平分∠ADC,EH⊥AD, EM⊥BC
