人教版数学八年级上册 12.2 课时1 全等三角形的判定(SSS) 课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.2 课时1 全等三角形的判定(SSS) 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 334.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 20:13:53 | ||
图片预览






文档简介
(共22张PPT)
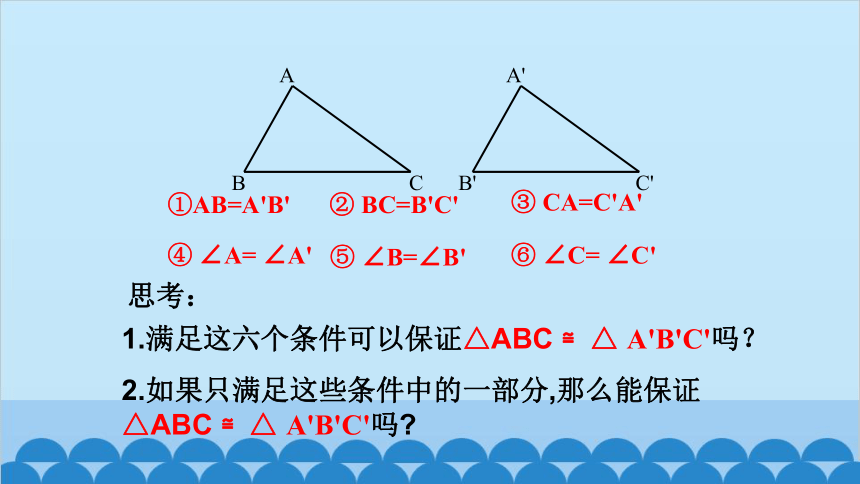
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形。
①AB=A'B' ② BC=B'C' ③ CA=C'A'
④ ∠A= ∠A' ⑤ ∠B=∠B ' ⑥ ∠C= ∠C'
A'
B'
C'
A
B
C
2、 已知△ABC ≌△ A'B'C',找出其中相等的边与角
12.2.1全等三角形的判定sss
A
B
C
A'
B'
C'
①AB=A'B'
③ CA=C'A'
② BC=B'C'
④ ∠A= ∠A'
⑤ ∠B=∠B'
⑥ ∠C= ∠C'
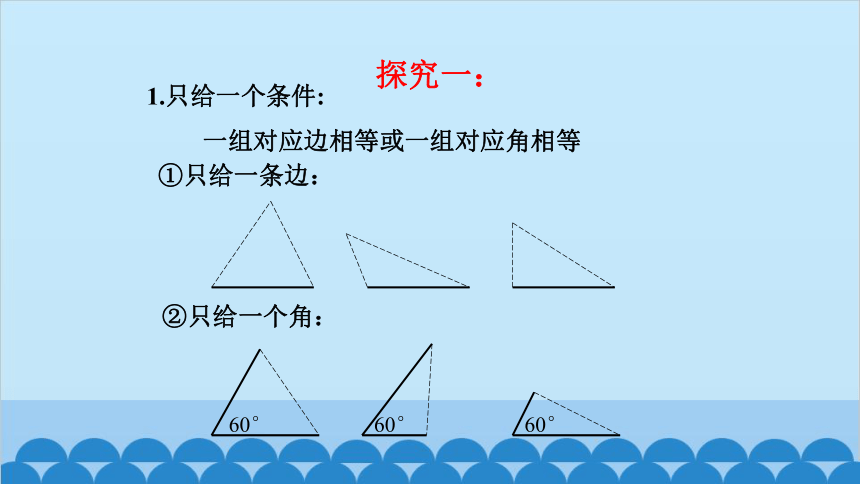
1.满足这六个条件可以保证△ABC ≌△ A'B'C'吗?
2.如果只满足这些条件中的一部分,那么能保证△ABC ≌△ A'B'C'吗
思考:
1.只给一个条件:
一组对应边相等或一组对应角相等
①只给一条边:
②只给一个角:
60°
60°
60°
探究一:
①两边;
③两角。
②一边一角;
2.如果满足两个条件?
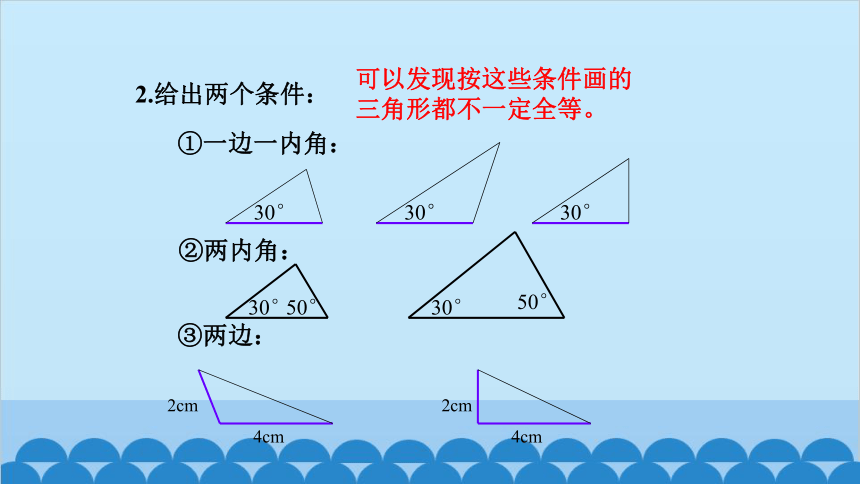
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按这些条件画的三角形都不一定全等。
两个条件
①两角;
②两边;
③一边一角。
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。
一个条件
①一角;
②一边;
3. 给出三个条件
(1)三条边
(2)三个角
(3)两角一边
(4)两边一角
先任意画出一个△ABC,再画出一个△A’B’C’ ,使
A’B’= AB ,B’C’ =BC, A’ C’ =AC.把画好△A’B’C’与同桌画的重叠,他们全等吗?
画法:
1.画线段 B’C’ =BC;
2.分别以 B’ , C’为圆心,BA,BC为半径画弧,两弧交于点A’;
3. 连接线段 A’B’ , A’C’ .
上述结论反映了什么规律?
探究二
三边分别相等的两个三角形全等。
(简写为“边边边”或“SSS”)
边边边公理:
注:这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。
如何用符号语言来表达呢
在△ABC与△DEF中
A
B
C
D
E
F
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF(SSS)
解: △ABC≌△DCB
证明:
AB = DC
AC = DB
=
SSS
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,
还需要条件
A
E
B D F C
A
B
C
D
想一想
△ABC ≌ ( )
1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等试说明理由。
△DCB
BC CB
BF=CD
或 BD=CF
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
归纳
自学课本37页的作图方法,思考云朵的问题,动手完成作图。
已知:∠AOB,求作:∠A′O′B′=∠AOB
(SSS)
A
B
C
D
拓展与提高:
如图,在四边形ABCD中AB=CD,AD=BC,
则∠A= ∠C.请说明理由。
解:在 ABD和 CDB中
AB=CD (已知)
AD=BC (已知)
BD=DB
(公共边)
∴ ABD ≌ CDB
∴ ∠A= ∠C ( )
全等三角形的对应角相等
练习: 已知:如图,AB=AD,BC=DC,
求证:△ABC≌ △ADC
B
A
C
D
AC
AC ( )
≌
AB=AD ( )
BC=DC ( )
∴ △ABC △ADC(SSS)
证明:在△ABC和△ADC中
=
已知
已知
公共边
A
B
C
D
在△ABD和△ACD中,
AB=AC (已知)
DB=DC (已知)
AD=AD (公共边)
∴△ABD≌△ACD (SSS)
∴ ∠B =∠C (全等三角形的对应角相等)
已知:如图,AB=AC,DB=DC,请说明∠B =∠C成立的理由
解:连接AD
已知:AC=AD,BC=BD,
求证:AB是∠DAC的平分线.
∵ AC=AD( )
BC=BD( )
AB=AB( )
∴△ABC≌△ABD( )
∴∠1=∠2
∴AB是∠DAC的平分线
A
B
C
D
1
2
(全等三角形的对应角相等)
已知
已知
公共边
SSS
(角平分线定义)
证明:在△ABC和△ABD中
当堂检测
见课本37页练习1、2题
备选题:如图,AB=AC,BD=CD,求证:∠1=∠2。
小 结
2. 三边对应相等的两个三角形全等(边边边或SSS);
1.知道三角形三条边的长度怎样画三角形。
3.体验分类讨论的数学思想
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形。
①AB=A'B' ② BC=B'C' ③ CA=C'A'
④ ∠A= ∠A' ⑤ ∠B=∠B ' ⑥ ∠C= ∠C'
A'
B'
C'
A
B
C
2、 已知△ABC ≌△ A'B'C',找出其中相等的边与角
12.2.1全等三角形的判定sss
A
B
C
A'
B'
C'
①AB=A'B'
③ CA=C'A'
② BC=B'C'
④ ∠A= ∠A'
⑤ ∠B=∠B'
⑥ ∠C= ∠C'
1.满足这六个条件可以保证△ABC ≌△ A'B'C'吗?
2.如果只满足这些条件中的一部分,那么能保证△ABC ≌△ A'B'C'吗
思考:
1.只给一个条件:
一组对应边相等或一组对应角相等
①只给一条边:
②只给一个角:
60°
60°
60°
探究一:
①两边;
③两角。
②一边一角;
2.如果满足两个条件?
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按这些条件画的三角形都不一定全等。
两个条件
①两角;
②两边;
③一边一角。
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。
一个条件
①一角;
②一边;
3. 给出三个条件
(1)三条边
(2)三个角
(3)两角一边
(4)两边一角
先任意画出一个△ABC,再画出一个△A’B’C’ ,使
A’B’= AB ,B’C’ =BC, A’ C’ =AC.把画好△A’B’C’与同桌画的重叠,他们全等吗?
画法:
1.画线段 B’C’ =BC;
2.分别以 B’ , C’为圆心,BA,BC为半径画弧,两弧交于点A’;
3. 连接线段 A’B’ , A’C’ .
上述结论反映了什么规律?
探究二
三边分别相等的两个三角形全等。
(简写为“边边边”或“SSS”)
边边边公理:
注:这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。
如何用符号语言来表达呢
在△ABC与△DEF中
A
B
C
D
E
F
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF(SSS)
解: △ABC≌△DCB
证明:
AB = DC
AC = DB
=
SSS
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,
还需要条件
A
E
B D F C
A
B
C
D
想一想
△ABC ≌ ( )
1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等试说明理由。
△DCB
BC CB
BF=CD
或 BD=CF
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
归纳
自学课本37页的作图方法,思考云朵的问题,动手完成作图。
已知:∠AOB,求作:∠A′O′B′=∠AOB
(SSS)
A
B
C
D
拓展与提高:
如图,在四边形ABCD中AB=CD,AD=BC,
则∠A= ∠C.请说明理由。
解:在 ABD和 CDB中
AB=CD (已知)
AD=BC (已知)
BD=DB
(公共边)
∴ ABD ≌ CDB
∴ ∠A= ∠C ( )
全等三角形的对应角相等
练习: 已知:如图,AB=AD,BC=DC,
求证:△ABC≌ △ADC
B
A
C
D
AC
AC ( )
≌
AB=AD ( )
BC=DC ( )
∴ △ABC △ADC(SSS)
证明:在△ABC和△ADC中
=
已知
已知
公共边
A
B
C
D
在△ABD和△ACD中,
AB=AC (已知)
DB=DC (已知)
AD=AD (公共边)
∴△ABD≌△ACD (SSS)
∴ ∠B =∠C (全等三角形的对应角相等)
已知:如图,AB=AC,DB=DC,请说明∠B =∠C成立的理由
解:连接AD
已知:AC=AD,BC=BD,
求证:AB是∠DAC的平分线.
∵ AC=AD( )
BC=BD( )
AB=AB( )
∴△ABC≌△ABD( )
∴∠1=∠2
∴AB是∠DAC的平分线
A
B
C
D
1
2
(全等三角形的对应角相等)
已知
已知
公共边
SSS
(角平分线定义)
证明:在△ABC和△ABD中
当堂检测
见课本37页练习1、2题
备选题:如图,AB=AC,BD=CD,求证:∠1=∠2。
小 结
2. 三边对应相等的两个三角形全等(边边边或SSS);
1.知道三角形三条边的长度怎样画三角形。
3.体验分类讨论的数学思想
